Робототехнический комплекс
Робототехнический комплекс – это система, которая состоит из манипуляционного механизма, ОУ и УУ.
Манипуляционный механизм – конструкция, предназначенная для перемещения и ориентации схвата (инструмента) в любую точку рабочей зоны.
ЧЭ – система технического зрения робота;
УПУ – управление ЭВМ, в памяти которой хранится информация об исходной пространственной ориентации зрения, а также его динамические свойства и расположение возможных препятствий внутри рабочей зоны. С учетом этой информации исполняются требуемые перемещения и углы поворота по различным степеням подвижности механизма. Результаты измерения передаются на ЦАП для получения аналоговых сигналов, которые приводят механизмы и управляемые органы в действие для управления всеми звеньями робота.
Математические модели объектов и сау
Для формализованного описания САУ используют три вида моделей (все они математические):
Модели представления системы во временной области – модели в пространстве состояний;
Модели представления системы в частотной области, получившие название вход/выход, получившие название операторная модель;
Структурные схемы – графические модели.
Для исследования процессов САУ необходимо в любом виде моделей составить описание ее в виде системы дифференциальных уравнений. Необходимо установить значение всех начальных условий, определить вид функций, описывающих внешнее воздействие.
Математическая модель сау в терминах преобразования «вход/выход»
В инженерной практике большое распространение получил операторный метод исследования системы, который использует некоторые специальные функции, характерные динамические свойства САУ, такие как передаточная функция, переходные функции и различные частотные функции.
Для этого метода справедливо:
Каждый реальный элемент САУ – это устройство, звено системы, в котором осуществляется образование одного воздействия (входного процесса) в другое (выходная реакция или выходной процесс);
Взаимодействие между звеньями создаются путем описания связей между их входами и выходами, определяющими структуру САУ.
Передаточная функция системы
Пусть нам задано, что рассматриваемая линейная функция САУ, для описания которой используется линейное дифференциальное уравнение, записываемое в следующем виде:
; 
;
,
где
и
– параметры системы.
Возьмем оператор дифференцирования для представления системы в операторной форме:
– оператор дифференцирования;
;
.
Перепишем используя оператор дифференцирования:
;
,
где
и
– многочлены
-ой
степени
;
.
Разделим левую и правую части операторной формы на :
;
Вводится операторная передаточная функция:
;
.
Представление системы в виде является символическим, оно не даст решения дифференциального уравнения, т.к. не определен смысл деления на .
Преобразования Лапласа
Если есть функция
,
которая называется оригиналом, то ей
ставится в соответствие функция
,
которая называется преобразованием
Лапласа функции
.
–
прямое преобразование Лапласа;
–
обратное преобразование Лапласа.
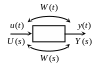
– образ входного сигнала;
– образ выходного сигнала.
Преобразование Лапласа даст возможность не решать рассматриваемое дифференциальное уравнение, а работать с алгебраической моделью (образами функций).
Используя преобразование Лапласа и … дает возможность записать операторную форму дифференциального уравнения в виде:
;
.
При нулевых начальных условиях
.
Передаточной функцией системы
(звена) называется отношение
-образа
сигнала на выходе
к
-образу
сигнала на входе
при нулевых взятых условиях:
Передаточная функция определяет характер связи.
Например,
;
.