Пример:

Представить в стандартной форме

;

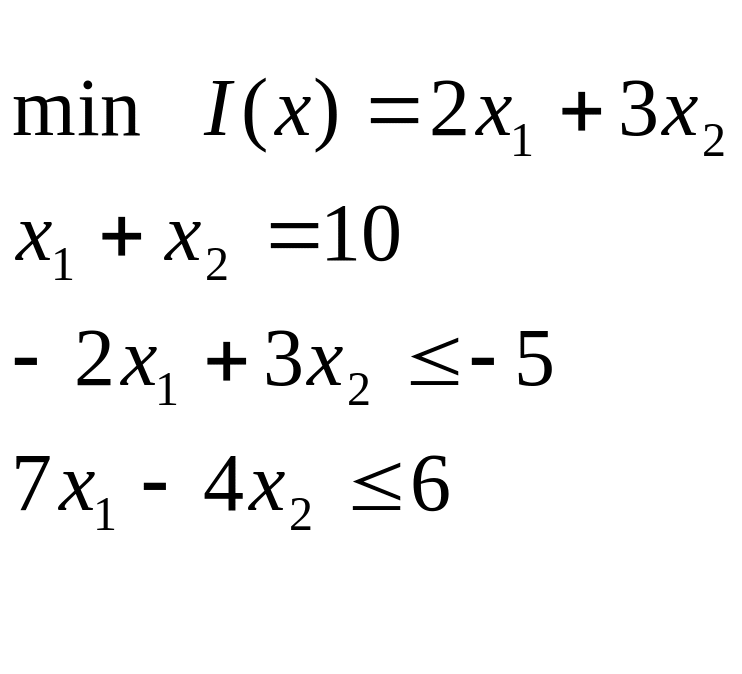где - не имеет ограничений в знаке

При анализе графического метода решения задач ЛП было отмечено, что оптимальному решению всегда соответствует одна из угловых (экстремальных) точек пространства решения . Именно этот результат и положен в основу S-метода. В S-методе реализуется упорядоченный процесс при котором, начиная с некоторой исходной (опорной), до,,,,, угловой точки, осуществляется последовательные переходы от одной экстремальной точки до другой, до тех пор, пока не будет найдена точка оптимального решения, Выбор каждой следующей точки определяется двумя параметрами :

• каждая последующая угловая точка должна быть смежна с предыдущей

• обратный переход к предшествующей экстремальной точки не может производиться

	свободные	базисные
A
B
C
D
E
F

Две закономерности:

1. Стандартная модель содержит 4 уравнения и 6 неизвестных ,а т.к. число уравнений должно быть равно числу неизвестных, то в каждой экстремальной точке 2-е переменные должны иметь нулевые значения

2. Смежные экстремальные точки отличаются только одной переменной в каждой группе (группы свободных базисных переменных)

Эти закономерности позволяют алгебраическим способом, путем преравнивания к нулю m-n переменных найти значения базисных переменных.

• если базисное решение удовлетворяет требованию неотрицательных правых частей, то оно называется допустимым базисным решением

Т.к. смежные точки отличаются только одной переменной- можно определить каждую последующую смежную экстремальную точку путем замены одной из текущих свободных переменных в базисные переменные (…)

Приложение Основные понятия линейной алгебры

Вырожденная матрица – квадратная матрица, у которой детерминант (определитель) равен 0.

Ранг матрицы – наибольший из порядков отличных от нуля миноров квадратной матрицы.

Транспонированная матрица – квадратная матрица, у которой столбцы и строки меняются местами.

Системы линейных уравнений: правило Крамера

Справочник по математике, страница 45.

Таблица преобразований Лапласа

3