Пример (продавец газет)

Пусть

– число газет, взятых продавцом;

– прибыль за проданную газету; – убытки за непроданную газету;

– спрос на газеты;

– плотность распределения спроса;

с – средняя прибыль, показатель эффективности продажи газет.

Составить математическую модель.

Дано:

, ; - количество продавцов

, ; - спрос (неуправляемая переменная, случайная величина)

;

. - (мат. ожидание)

Решение:

Два случая:

1. все газеты продаются ;

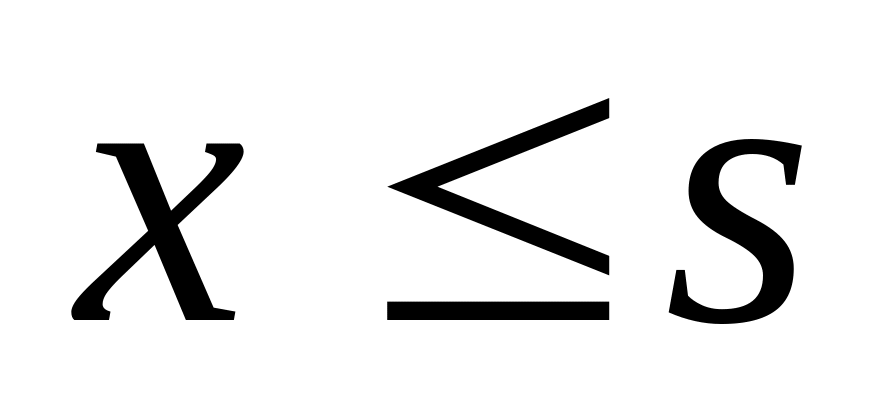2. газеты не продаются .

;

.

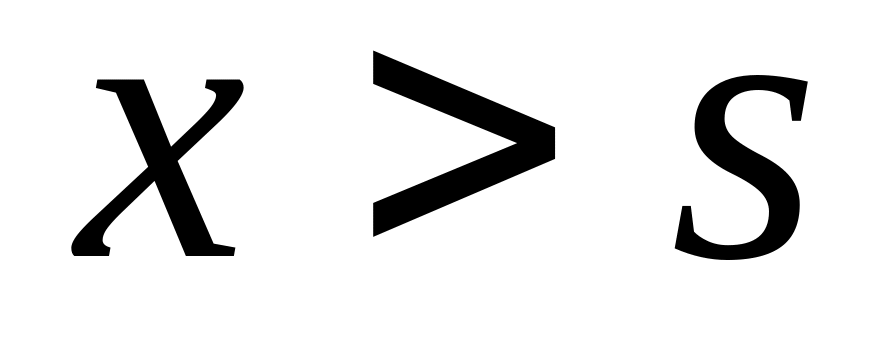Пример

Предприятие изготавливает два вида красок:

• для наружных работ (краска 1-го вида)

• для внутренних работ (краска 2-го вида)

Продукция обоих видов поступает в продажу.

Для производства обоих видов красок используется два исходных продукта A и B.

Максимально возможные суточные запасы этих продуктов 6 и 8 тонн соответственно.

Расходы A и B на одну тонну соответствующих красок даны в таблице.

Исходный продукт	Расход исходного продукта в тоннах на 1 тонну продукта		Максимально возможный запас
	краска 1-го вида	краска 2-го вида
A	1	2	6
B	2	1	8
опт. цена	3 тыс. $	2 тыс. $

Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида не превышает суточный спрос на краску 1-го вида более чем на 1 тонну.

Кроме того, установлено, что спрос на краску 2-го вида не превышает 2 тонны в сутки.

Оптовые цены за 1 тонну равны.

Какое количество краски каждого вида должно производить предприятие чтобы получить максимальный доход от реализации.

Составить математическую модель.

Дано:

, ; - количество произведенной продукции (краски) (в тоннах)

, ; - спрос (в тоннах)

;

Решение:

;

;

.

.

.

Из всех программ принадлежащих множеству надо выбрать такую, которая бы соответствовала .

;

; - число ограничений

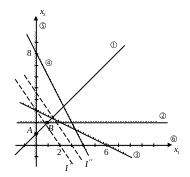
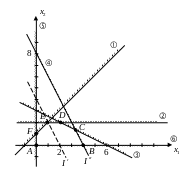
Ограничения и линейные, значит можно применить метод линейного программирования.

Графический метод линейного программирования. (Он может быть использован, если ).

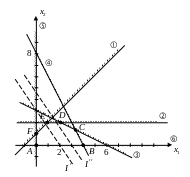
Пространство содержит бесконечное число допустимых решений соответствующих точкам многоугольника , а нам надо найти оптимальное решение, для этого необходимо определить в каком направлении возрастает целевая функция .

При графическом решении надо нанести ряд параллельных прямых соответствующих целевой функции при нескольких произвольных возрастающих значениях , что позволит определить наклон целевой функции и направление в котором происходит ее увеличение.

; ;

; .

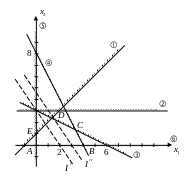
Найдем координаты точки :

;

;

; ;

;

;

;

.

Определить и найти оптимальное решение , считая что каждое из указанных ниже условий заменяет, а не дополняет соответствующие исходные данные, причем все остальные заданные соотношения остаются неизменными.

1. максимальный спрос на краску 2-го вида равен 3 тонны в сутки;

2. спрос на краску 2-го вида не менее 2 тонн в сутки;

3. спрос на краску 2-го вида ровно на 1 тонну превышает спрос краски 1-го типа;

4. допустимый суточный расход исходного продукта 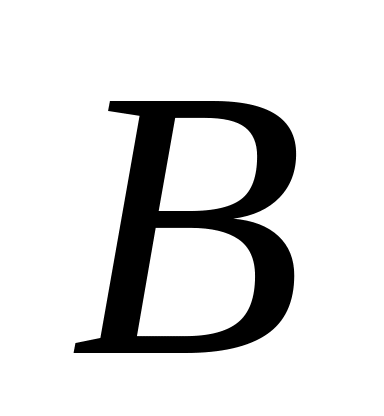не меньше 8 тонн в сутки;

5. допустимый суточный расход исходного продукта не меньше 8 тонн, а спрос на краску 2-го вида превышает спрос на краску 1-го вида не менее чем на 1 тонну.

6. найти оптимальное решение при следующих значениях целевой функции: ;

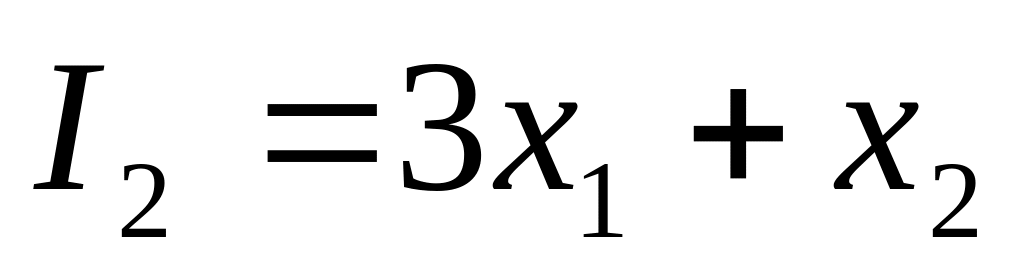7. найти оптимальное решение при следующих значениях целевой функции: .

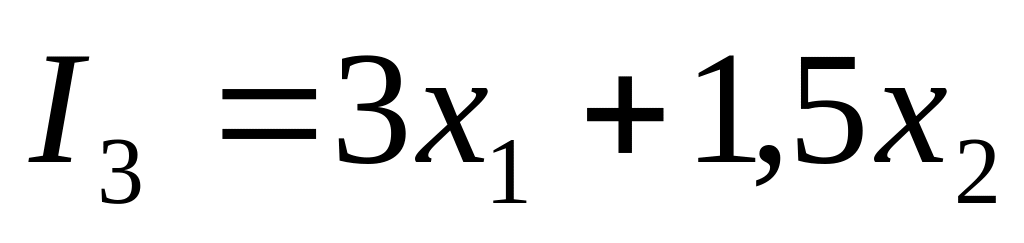Пример с условием 1

Решение:

.

.

; ;

; .

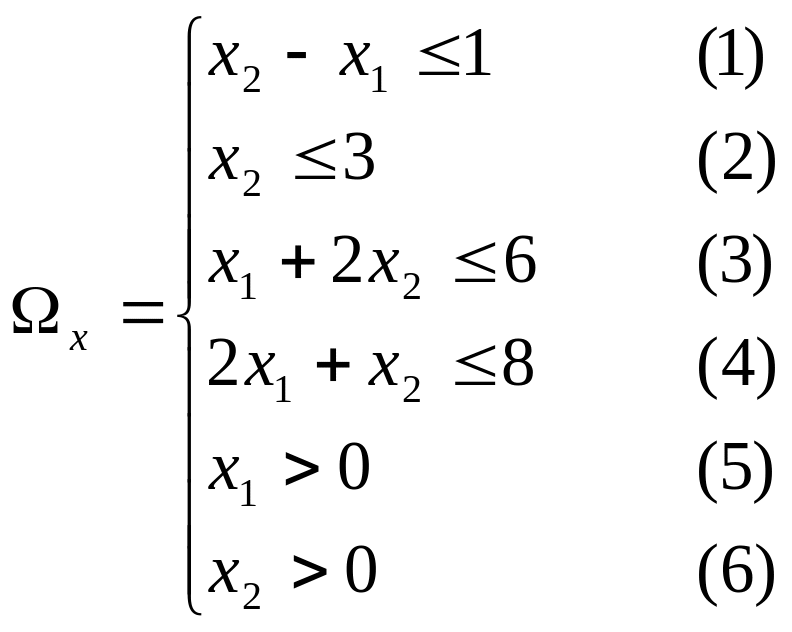Найдем координаты точки :

;

;

; ;

;

;

;

.

Пример с условием 2

Решение:

.

.

; ;

; .

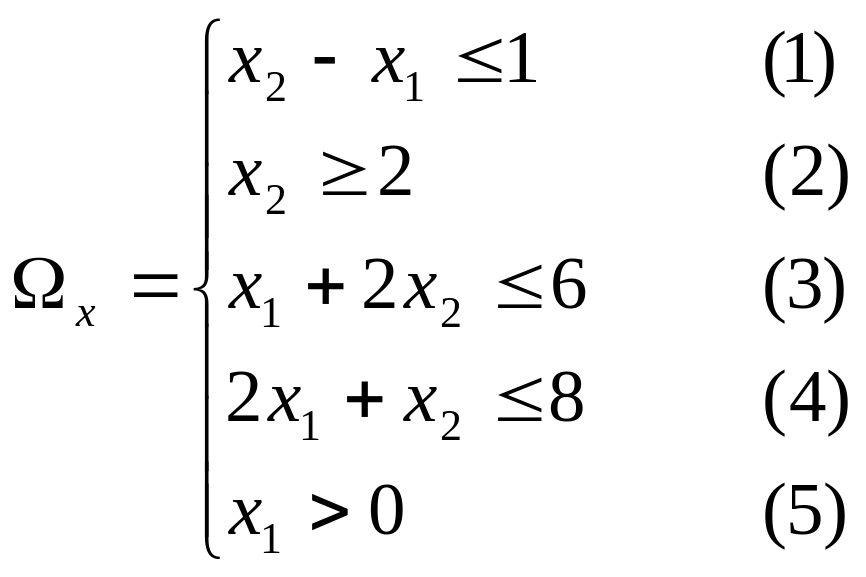Найдем координаты точки :

;

;

;

;

.

Пример с условием 3

Решение:

.

; ;

; .

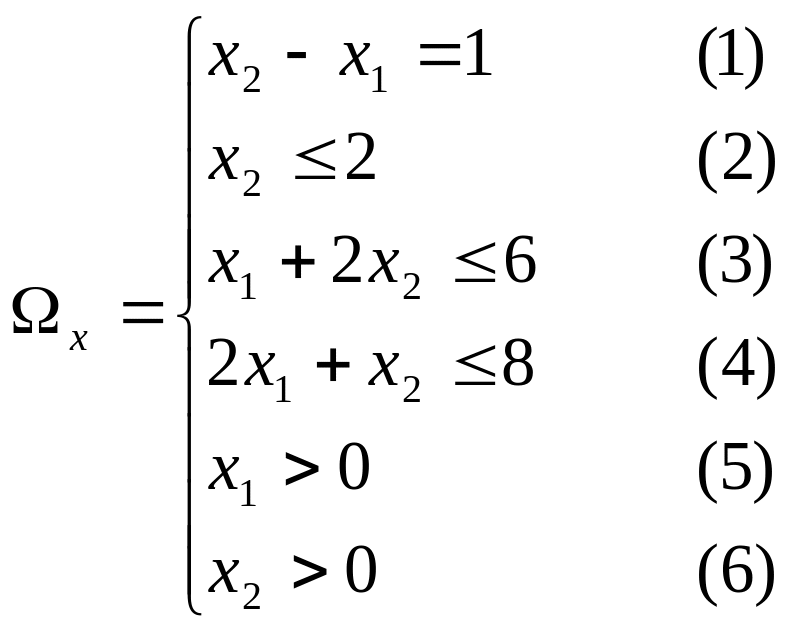
Найдем координаты точки :

;

;

;

;

.

Пример с условием 4

Решение:

.

.

; ;

; .

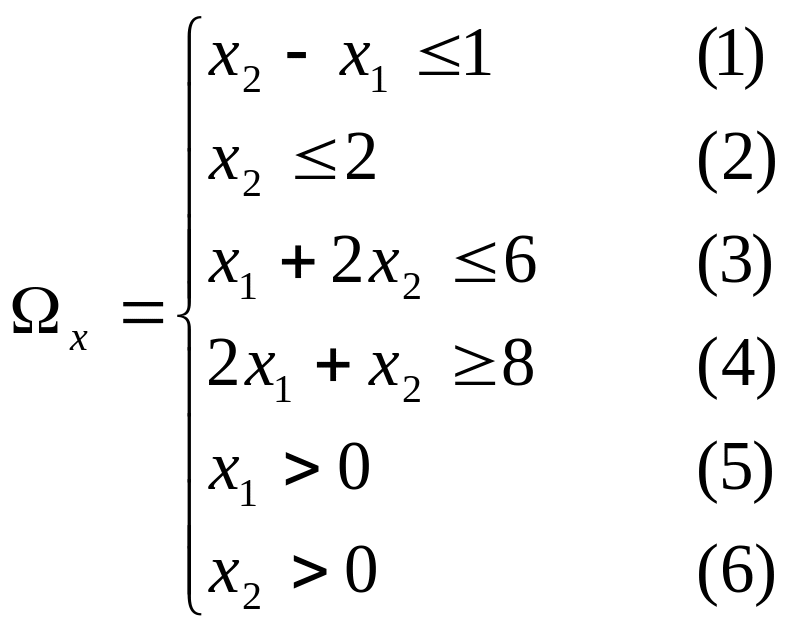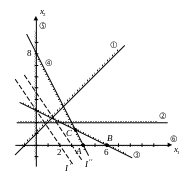
Найдем координаты точки :

;

;

;

;

.

Пример с условием 5

Решение:

.

.

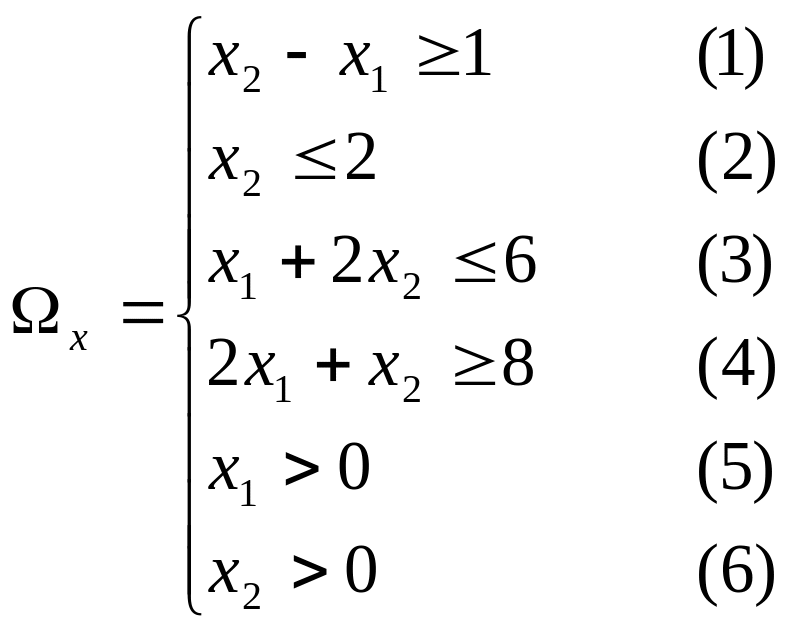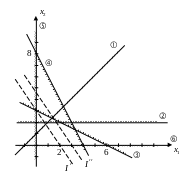
Нет допустимых решений.

Пример с условием 6

Решение:

.

.

; ;

; .

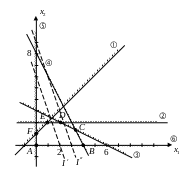
Найдем координаты точки :

;

;

;

;

.

Пример с условием 7

Решение:

.

.

; ;

; .

.

Алгебраический метод решения задач линейного программирования (симплекс метод)

Возьмем систему из последнего домашнего задания

Общий метод решения задач ЛП называется Simplex(S)-метод. Информацию которую можно получить, не ограничивается оптимальными значениями переменной и т.к. он позволяет дать экономическую интерпретацию полученного решения и провести анализ модели на чувственность. S-метод носит итерационный характер: однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор пока не будет получено оптимальное решение. Для использования S-метода, мат. модель должна быть представлена в форме, которую называют линейной формой:

• все ограничения должны быть записаны в виде равенств с неотрицательной правой частью

• значения всех переменных должны быть неотрицательны

• целевая функция подлежит максимилизации и минимализации

Как привести математическую модель к стандартной форме:

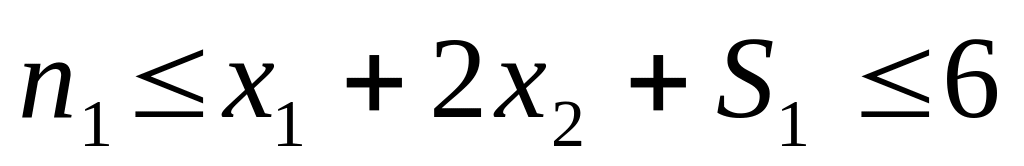
1. Для ограничения: меньше/равно - остаточная переменная 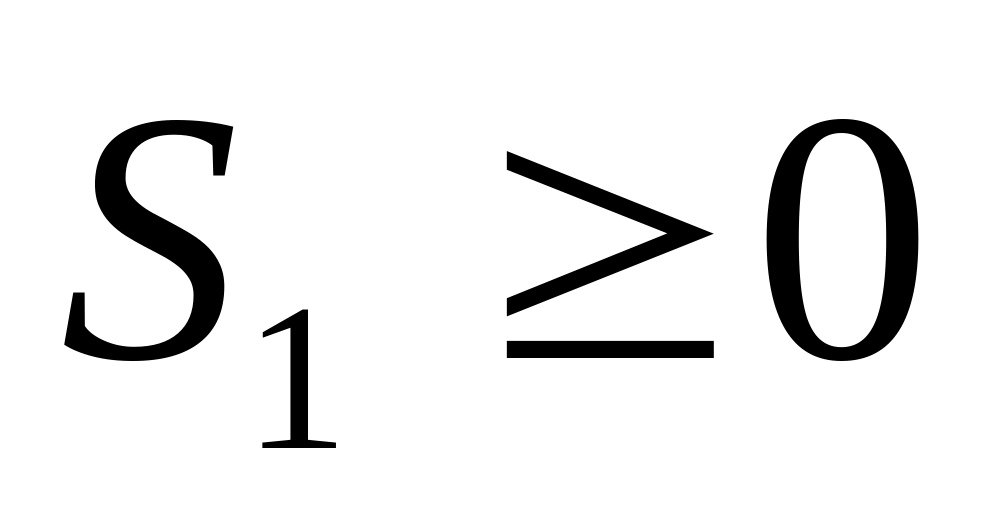- превращает ограничения типа неравенство в равенство и ее можно интерпретировать как остаток или неиспользованную часть ресурса

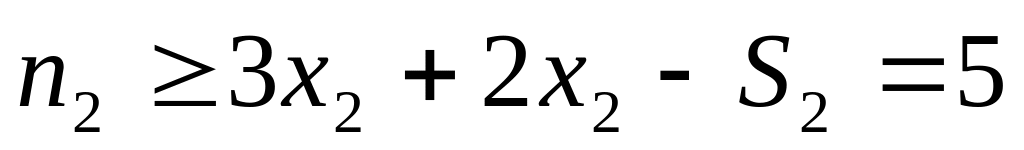
2. Если ограничения: больше/равно, то для приведения к стандартному виду вычитается перемена, которая называется избыточная 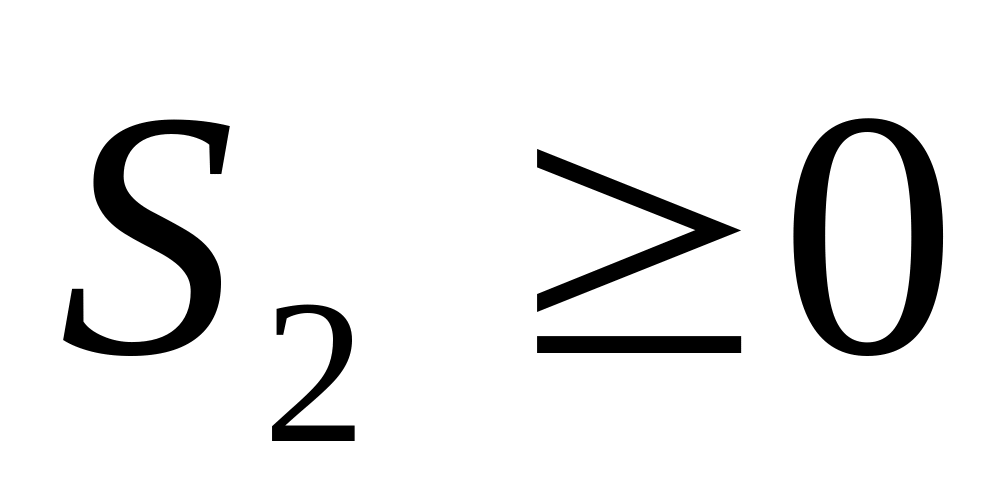//из левой части вычитаем

Преобразования целевой функции