Стабилизирующая обратная связь по наблюдениям выходного сигнала (при включении наблюдателя в обратную связь)
Объединение управляющей системы ее наблюдателя и контура отрицательной обратной связи представляет собой дуальную систему, т.е. имеет регулятор и наблюдатель.
;
– желаемое состояние (значение)
;
;
– ошибка управления
; 
;
Система управляемого объекта
;
;
Сделаем замену когда
;
;
;
Запишем их векторно-матричной форме
;
– уравнение динамики дуальной системы;
– матрица динамики системы с регулятором и наблюдателем.
Собственные числа равны собственным числам матриц динамики, расположенных на главной диагонали.
Матрица
характеризует свойства системы с
регулятором и наблюдателем, ее собственные
числа совпадают с собственными числами
матриц расположенных на диагонали, т.е.
и
.
При выполнении условий не вырожденности
пар матриц
и
и
могут быть выбраны так, чтобы собственные
числа матрицы дуальной системы имели
отрицательные вещественные части и тем
самым обеспечивали стабилизацию дуальной
системы в целом.
В целом структурная схема замкнутой дуальной системы будет иметь вид:
;
.
Алгоритм построения регулятора и наблюдателя
; 
.
Преобразовать матрицу
в столбец
путем замены
;
при
умножении на которую справедливо, что
пара матриц
не вырождена.
(последний шаг)
;
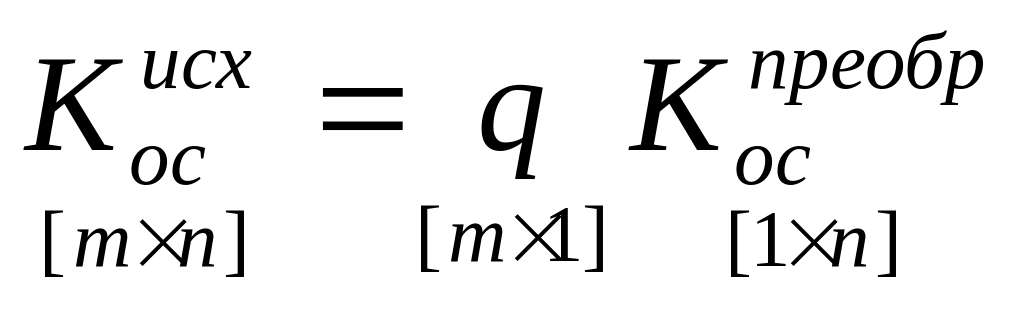Пример
Дана система производства и управления
запасами, в которой объем выпускаемой
продукции
,
а объем запасов
.
– интенсивность производства;
– объем поставок производства.
Рассматривается непрерывный характер производства, которому соответствует следующая модель:
;
;
; 
.
Необходимо:
Оценить устойчивость системы;
Построить переходный процесс обусловленный ненулевыми начальными условиями;
Построить стабилизирующую отрицательную обратную связь.
Решение:
;
;
; 
;
.
Преобразуем матрицу в столбец
;
Определим
управляемость системы:
;
.
Определим характеристические числа
;
;
;
.
Найдем
коэффициенты характеристического
уравнения:
;
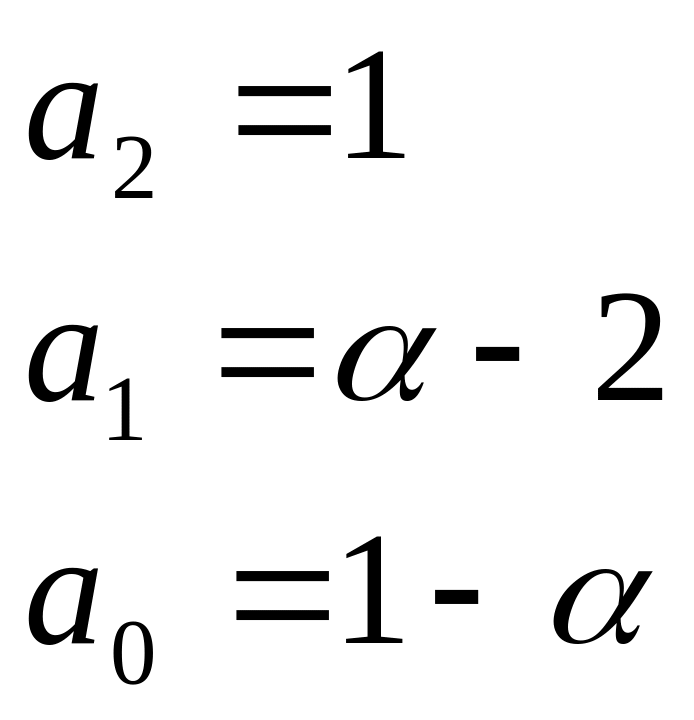
Пусть Зададим и Находим коэффициенты характеристического уравнения желаемой системы ;
Вычисляем матрицу
;
;
.
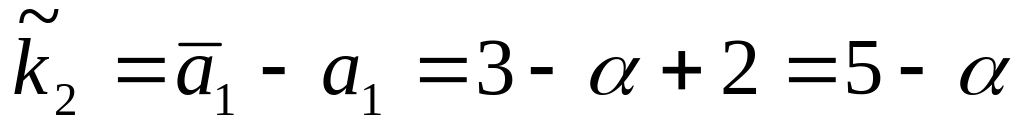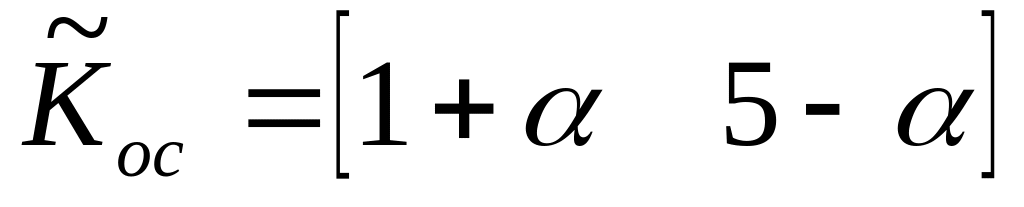Вычисляем матрицу перехода к новому базису
;
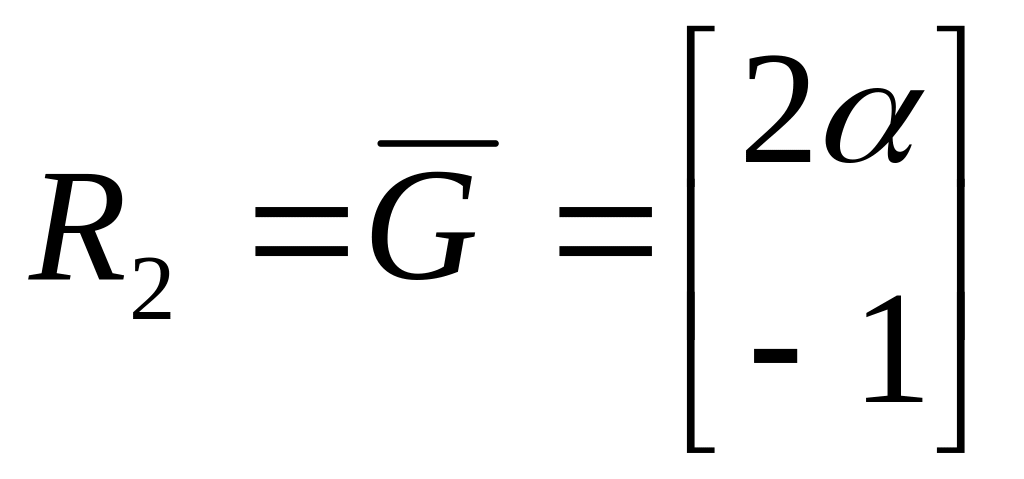Невозможно слагать матрицы разных размерностей.
Оптимальное управление сау
– наилучшая управляемость системы
– оптимальная траектория движения системы
– функционал (оптимальное значение)
В задачах детерминированного синтеза
выделяют задачу построения оптимальных
траекторий УУ
,
т.е. определение оптимального управления
.
Задача оптимизации заключается в том, как что-либо делать наилучшим образом. В ТУ «что-либо делать» означает управлять динамической системой.
При выборе управления не существует абсолютной оптимизации, поэтому при выборе наилучшего управления необходимо определить понятие оптимизации. Для этого с каждой задачей управления, стабилизации, идентификации связывают некоторое число, которое называют показателем качества. Значение этого показателя качества есть мера того, на сколько должно управление обеспечивать функционирование системы по отношению к выбранным критериям. Показатель качества – это математическая модель требований качества, средство оценки желаемого характера поведения системы.
Экстремальное значение показателя качества – это критерий качества функционирования, обозначим (критерий, который определяет доход или стоимость для любого предложенного закона управления называют функцией стоимости или целевой функцией).
В задачах оптимального управления задают две проблемы:
Выбор математической модели, в состав которой входит выбор функционала, который зависит от выбора управляющего показателя качества воздействия, состояния системы
.
Определить состав ограничений, в
пределах выполнения которых может быть
реализована траектория движения системы
(и в первую очередь это ограничение
связано с обеспечением траектории
движения системы).Выбор математического метода для решения задачи оптимального управления. В общем случае решения поставленной задачи не существует. Так как задача является вариационной, то решение даже вариационными методами трудное, а иногда даже не возможное. Поэтому были разработаны новые методы для задач оптимального управления САУ, к ним относятся: методы Калмана; принцип максимума Понтрягина; методы динамического программирования Беллмана.