Алгоритм построения регулятора

1. Определить управляемость системы. невырожденность пары матриц ; ; .

2. Определить характеристические числа , матрицы динамики исходной системы . Если их значения соответствуют требованиям начальной фундаментальной системы , то строить регулятор не надо. В противном случае найти коэффициенты характеристического уравнения 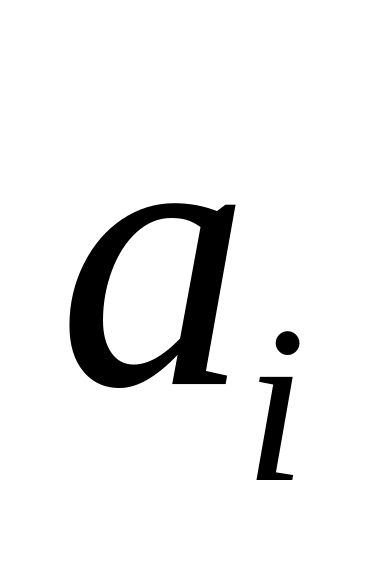, . Согласовать значение .

3. Задать требуемое значение характеристических векторов , . Найти требуемые коэффициенты характеристического уравнения . ; .

4. Вычислить элементы матрицы , ; .

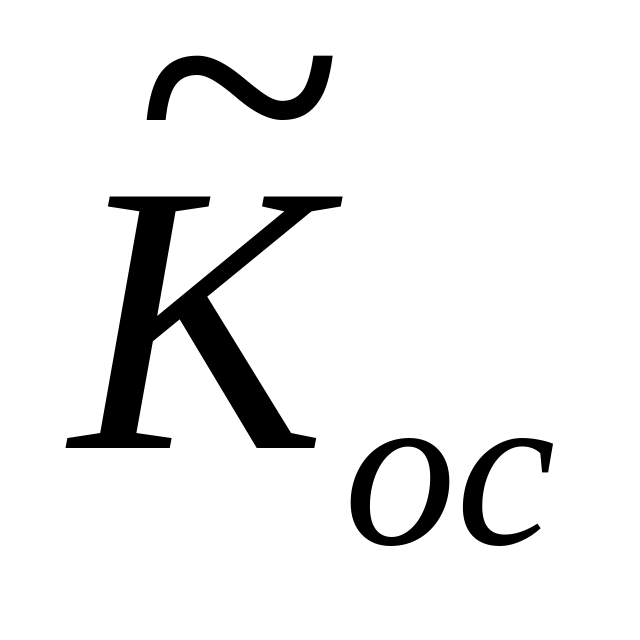5. Вычислить матрицу перехода к новому базису . ; .

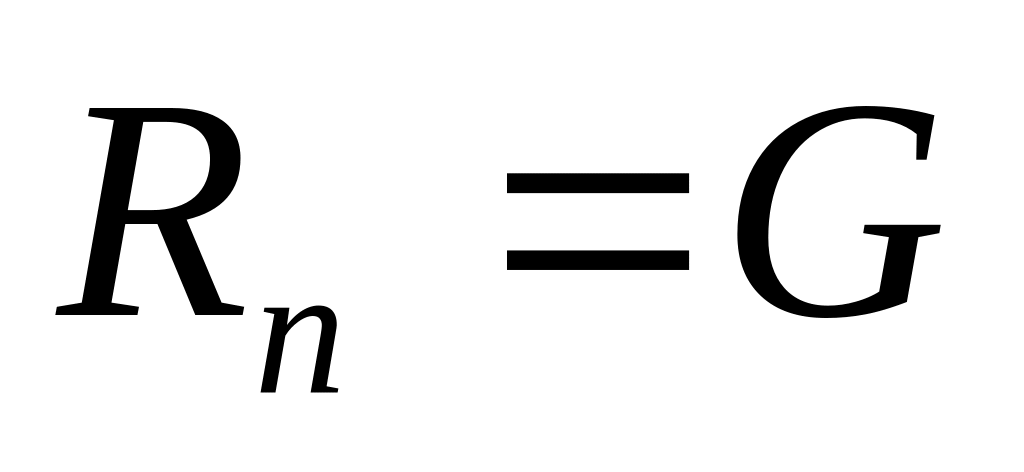6. Вычислить матрицу в старом базисе .

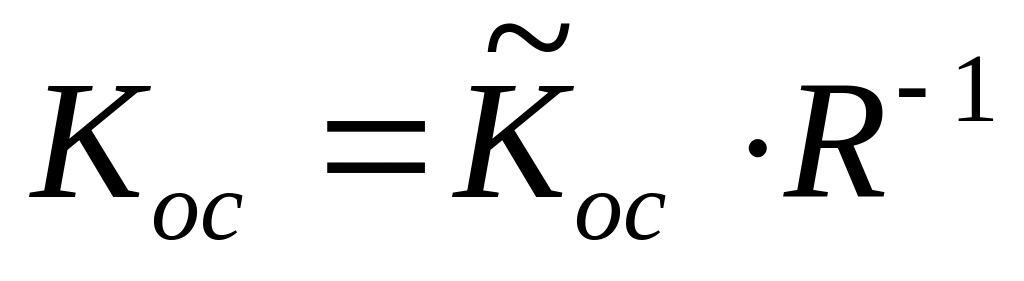7. Построить регулятор, для которого объект управления задается матрицей динамики 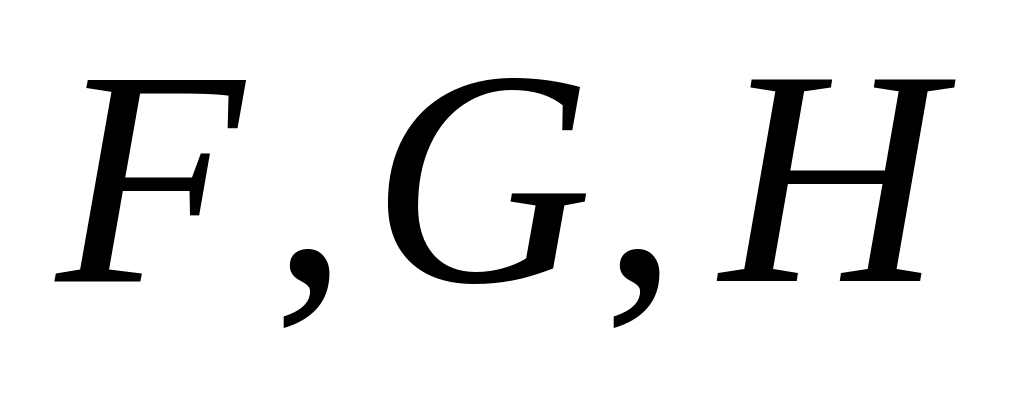, для которого ; . Проверить динамические свойства системы с регулятором.

Пример

Задана исходная система:

; ;

;

Решение:

1. Строим матрицу управления Это одномерная система, т.к. величины скалярные. , , 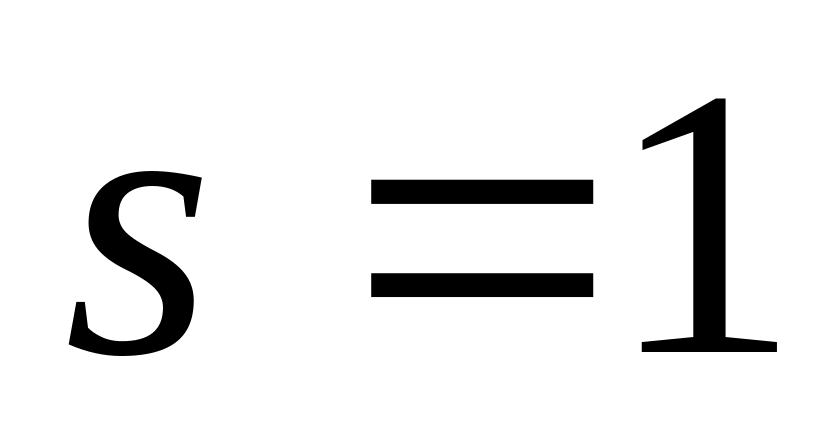. 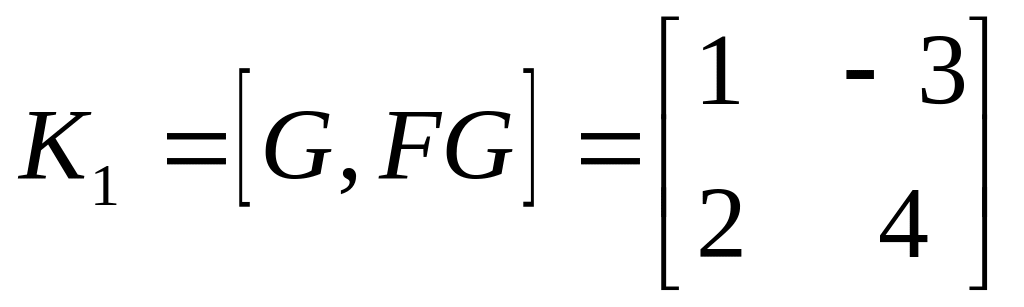; система управляема.

2. Найдем характеристические числа матрицы динамики исходной системы : ; ; 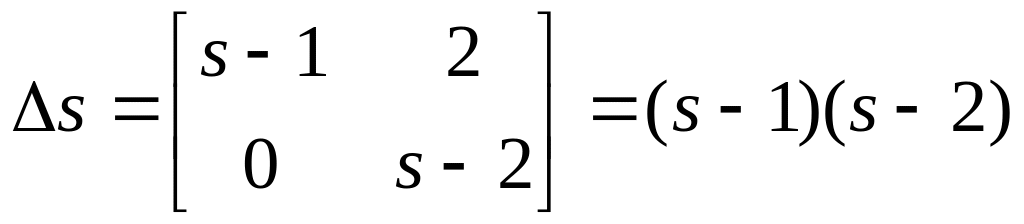; ; ; ; 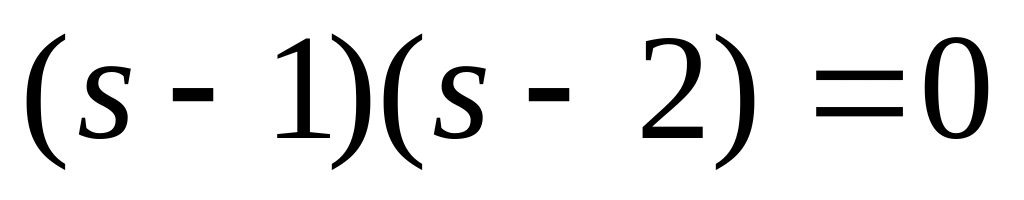; 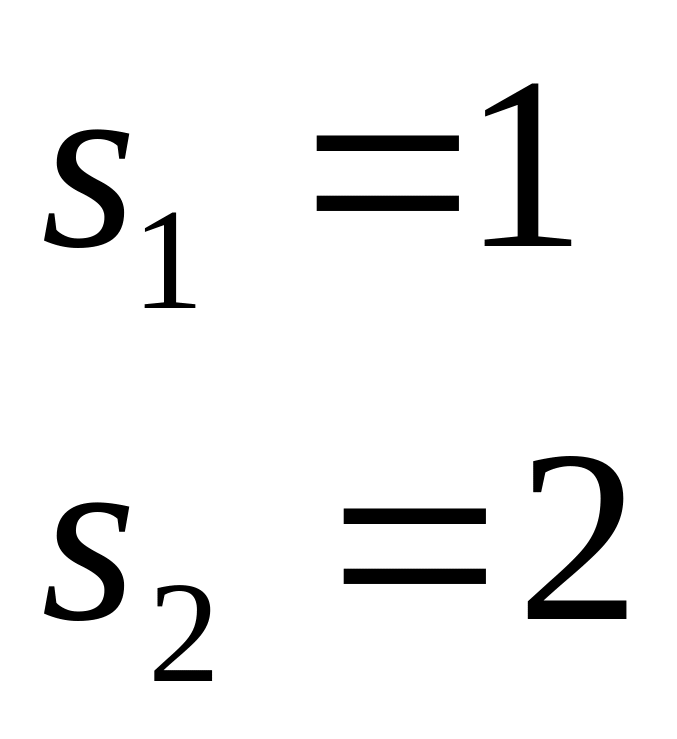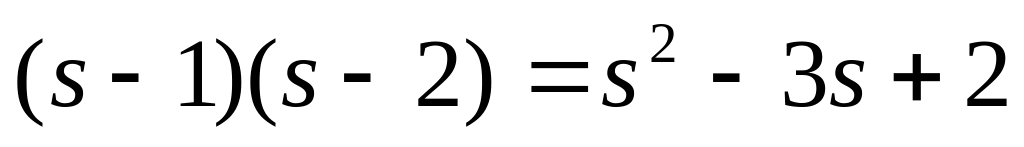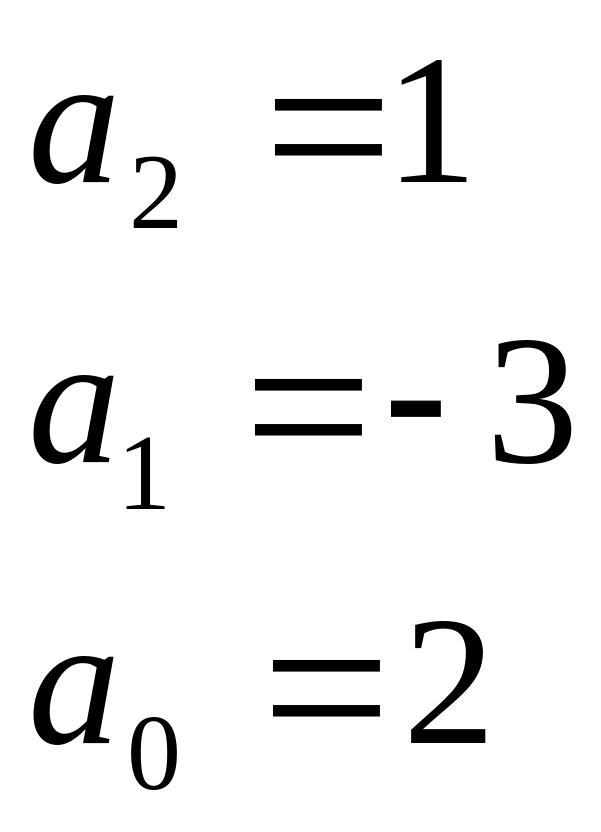– система устойчива. Пусть запас устойчивости .

3. Зададим 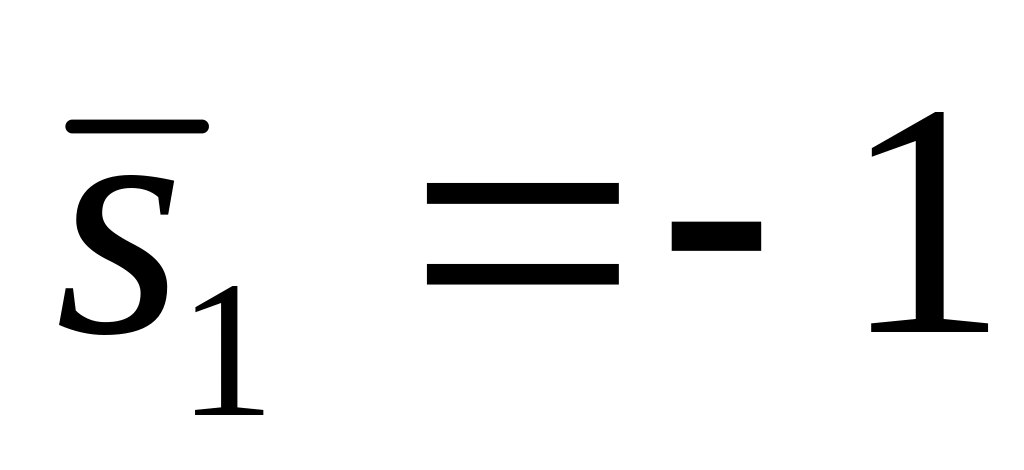и Находим коэффициенты характеристического уравнения желаемой системы: ;

4. Вычисляем матрицу ; ; .

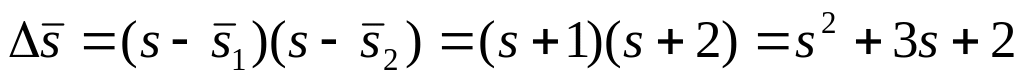5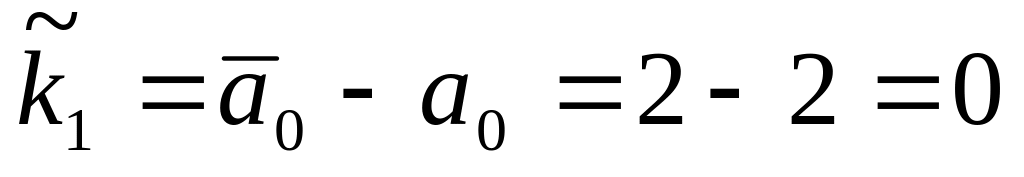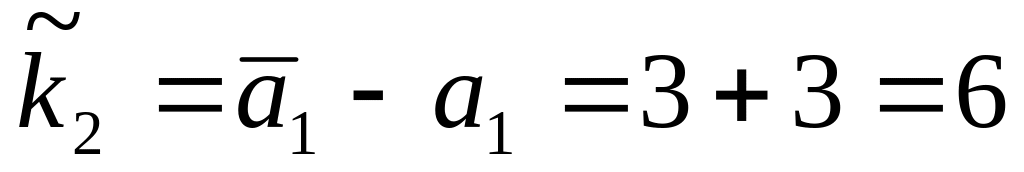. Вычисляем матрицу перехода к новому базису : ; ; .

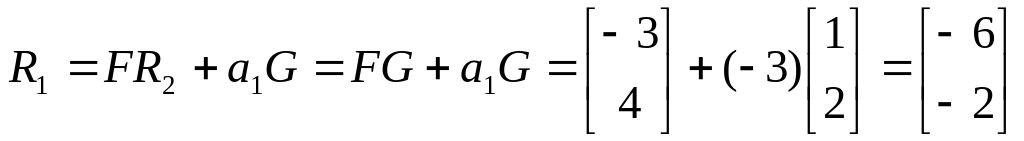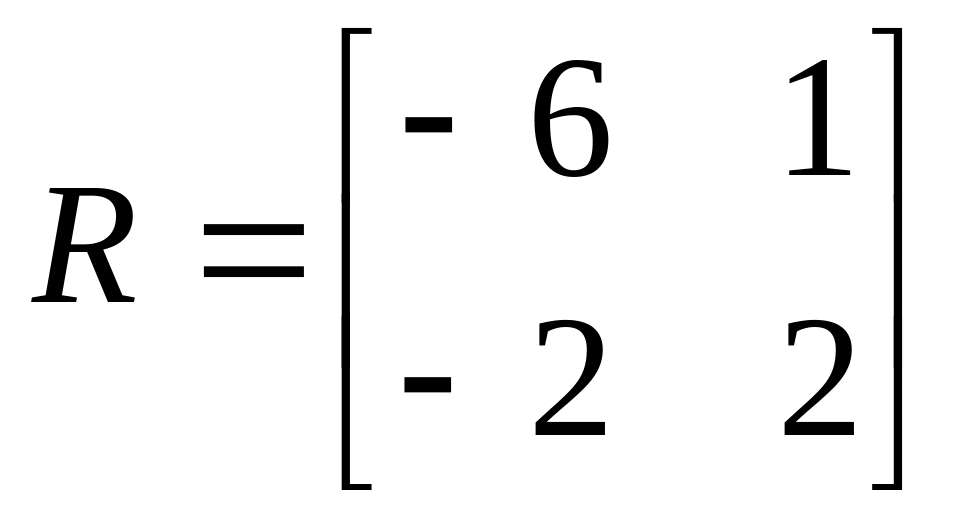6. Вычислим матрицу 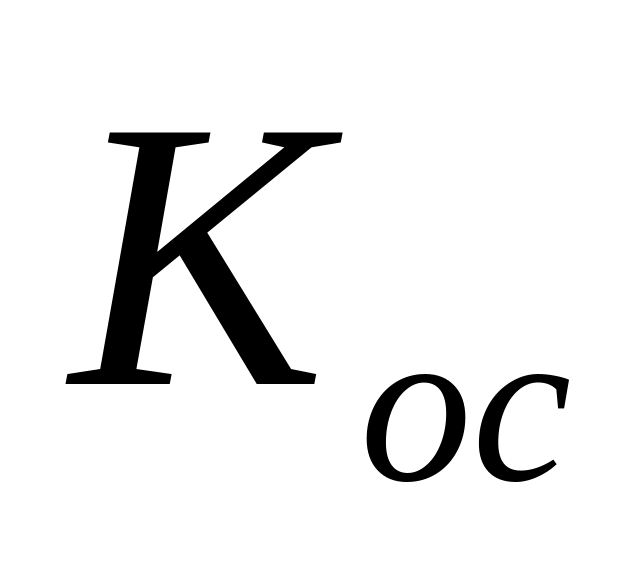в старом базисе: ; ; ; ; .

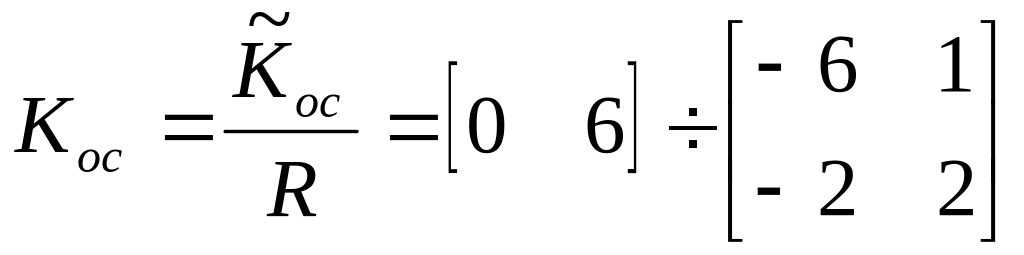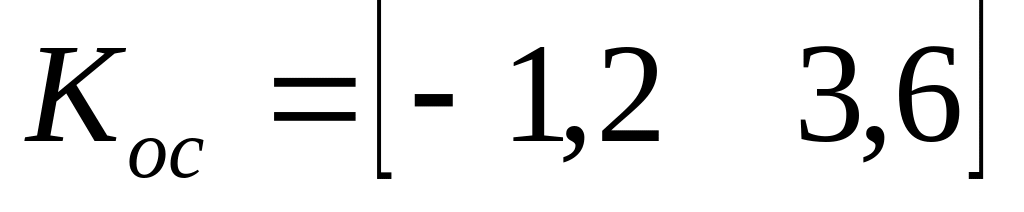7. Построим регулятор ; ; ; ; ;

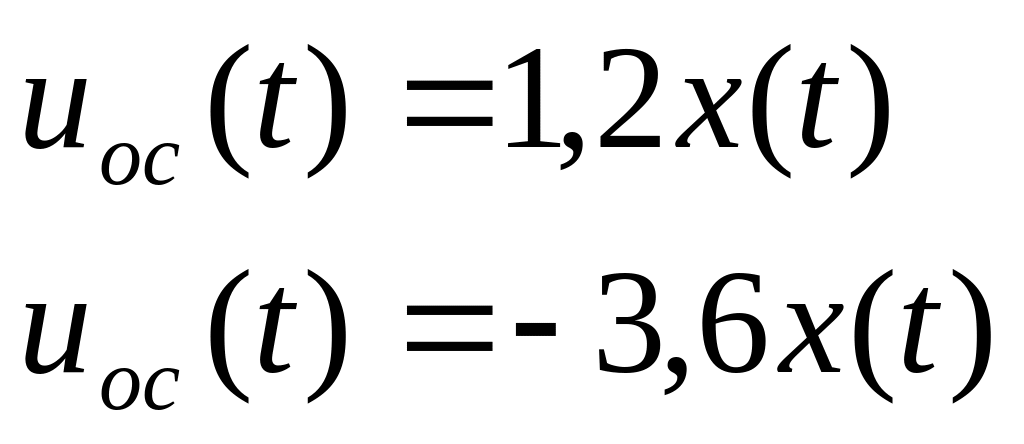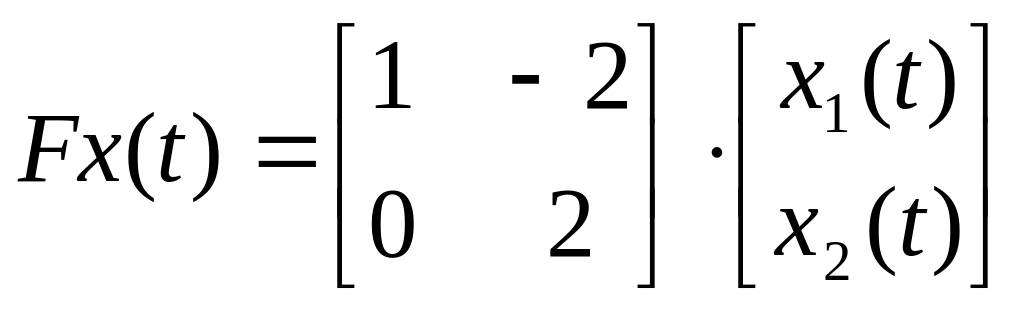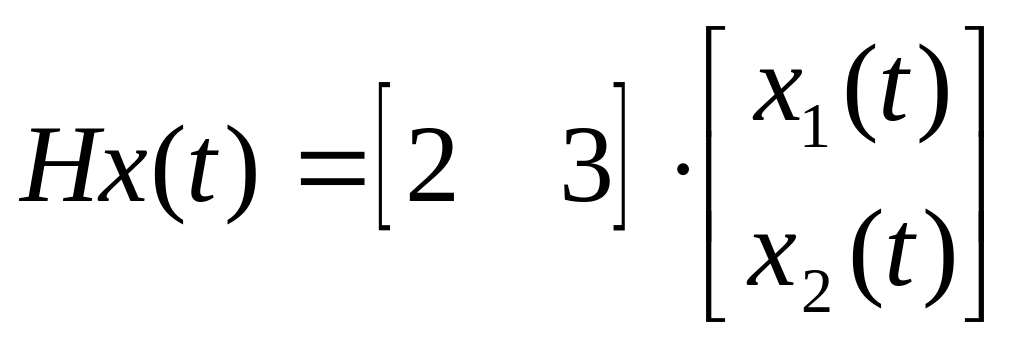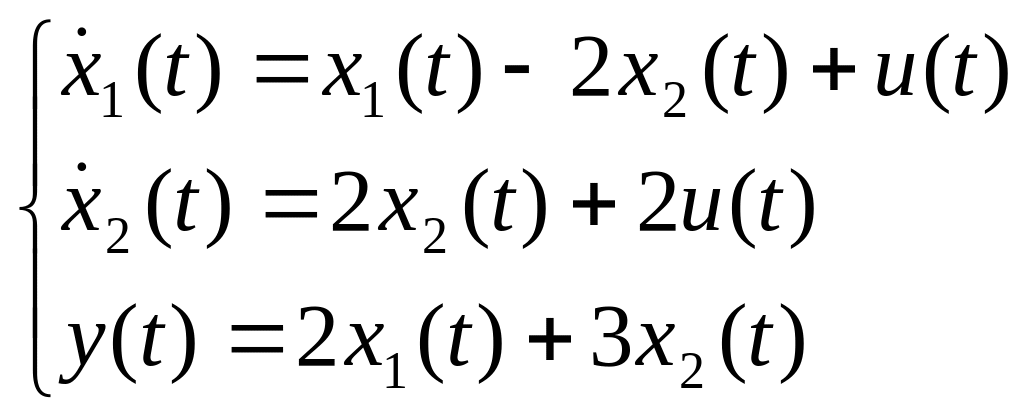Стабилизация системы с помощью отрицательной обратной связи в условиях неполной информации

Линейную систему с помощью ООС по состоянию можно перевести в состояние покоя , причем этому движению можно придать любые динамические свойства. Эту возможность можно реализовать, имея полную информацию о состоянии системы, но в реальности часто нет возможности прямого измерения всего вектора состояния.

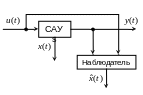
Если нельзя измерить, то оказывается можно построить динамическую линейную систему – наблюдатель, выходные переменные которой асимптотически приближаются к координатам состояния управляемой системы.

; – ошибка оценки (значений) вектора состояний

;

.

Наблюдатель линейной системы Теорема

Пусть есть возможность точного измерения выходного сигнала в любой момент времени . При выполнении условия не вырожденности пары матриц по измерениям выходного сигнала можно восстановить состояние системы, используя идею обратной связи.

Устройство оценки вектора состояний по измерениям входных и выходных переменных объекта называется наблюдателем непрерывного типа -го порядка. Наблюдатель описывается следующими линейными дифференциальными уравнениями:

;

На вход подается сигнал, равный разности измерения и прогнозного значения :

;

Рассогласование этих сигналов определяемое значениями матрицы наблюдателя и формирует сигнал ООС.

;

, где

.

Есть один объект и два наблюдателя.

;

; – дифференциальное уравнение относительно ошибки

– матрица динамики наблюдателя

Если собственные числа матрицы наблюдателя будут находиться в левой полуплоскости, то динамические свойства наблюдателя обеспечат асимптотическую устойчивость, при которой ошибка оценки .

Как определить матрицу и ее элементы, чтобы матрица наблюдателя была асимптотически устойчива?

;

;

;

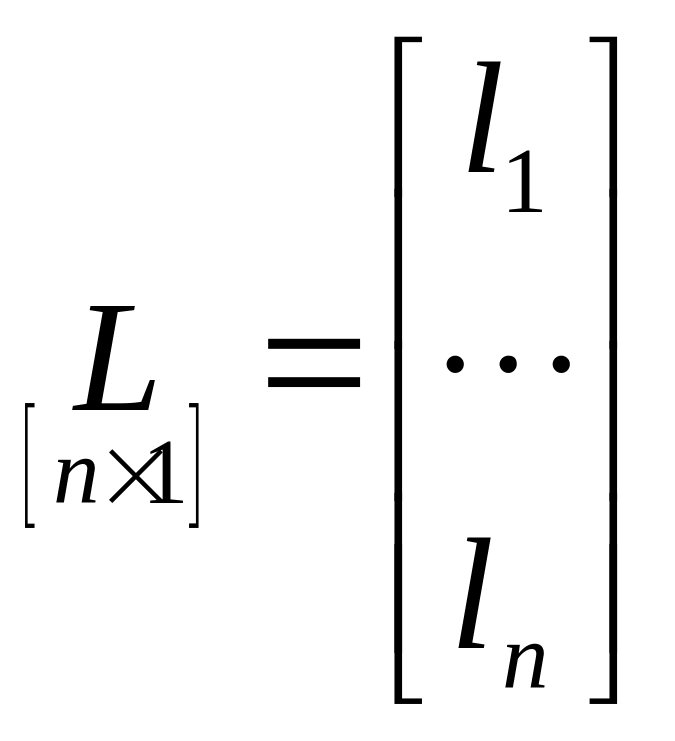и – собственные числа одни и те же

;

Регулятор Наблюдатель

Собственные числа: Собственные числа:

Такое представление для выбора матрицы наблюдателя позволяет воспользоваться алгоритмом построения регулятора, произведя следующие замены в исходном алгоритме:

1. 

2. 

Вместо проверки управляемости по паре произвести проверку наблюдаемости по паре и если система наблюдаема, то осуществить переход к новому базису, в результате которого вместо определения матрицы осуществить вычисление элементов транспонированной матрицы .

Основные выводы:

Наблюдатель является реализуемым устройством в соответствии со структурой схемы, т.к. он состоит из интеграторов и усилителей, на входе наблюдателя сигнал обратной связи, пропорциональный разности между измеренным сигналом на выходе и прогнозируемым его значением.

3. Оценка вектора состояния может быть получена при произвольных начальных условиях. Так как оценка строится аналогично по тем же матрицам и внешнему воздействию , то наблюдатель -го порядка является моделью управляемого объекта.