Теорема Калмана для оценки наблюдаемости

Для того чтобы линейная стационарная система была полностью наблюдаемой необходимо и достаточно, чтобы ранг матрицы наблюдаемости , определяемой блоками

был равен порядку системы .

Если , то система является не полностью наблюдаемой.

Пример

.

Решение:

; ; ;

; ;

.

;

система не наблюдаемая.

Синтез сау

Степень устойчивости – расстояние ближайшего характеристического числа до мнимой оси.

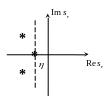
– запас устойчивости;

Программа управления и законы управления должны обеспечивать требуемую точность функционирования системы, устойчивость и качество управления.

Различают законы управления:

• Линейные;

• Нелинейные;

• Временные;

• Параметрические.

Линейные законы определяются линейными законами, нелинейными уравнениями и формируются конкретными техническими устройствами, регуляторами, специальными процессами и другое.

Синтез сау с помощью отрицательной обратной связи для стабилизации системы.

– желаемое значение

Возможно построить такое

, где

– сигнал обратной связи, который строится как линейная комбинация, задаваемая матрицей обратной связи.



Устройство, формирующее сигнал в виде матрицы обратной связи называется регулятором n-ого порядка.

– оценка вектора состояния.

Принцип детерминированного синтеза в ТУ означает нахождение управляющего воздействия , при котором управляемая переменная и компоненты вектора состояния удовлетворяют заданным значениям и . Если задающее воздействие и конечные значения начального состояния в точке 0, то и при должны быть равны 0, т.е. система должна быть асимптотически устойчивой.

Одним из способов обеспечения устойчивости, стабилизации заданного движения системы является введение отрицательной обратной связи такой, что

, где

– представляет собой линейную комбинацию компонентов вектора состояния, определяется по формуле .

Матрица формируется устройством и назначена для синтеза управления, называемым регулятор.

При построении законов управления различают 2 случая:

1. синтез управления при возможности измерения всех переменных состояния (в условиях полной информации);

2. синтез в условиях неполной информации, не все переменные состояния измеряемы, но система является наблюдаемой.

Рассмотрим первый случай.

При ,

Задача синтеза состоит в том, чтобы выбрать матрицу обратной связи таким образом, чтобы матрица динамики системы с регулятором обеспечивала стабилизацию (асимптотическую устойчивость) системы, т.е. это означает, что матрица обратной связи должна иметь собственные числа хорошие (в отрицательной плоскости и обеспечить необходимый запас устойчивости ).

Теорема

Можно показать, что необходимым и достаточным условием разрешимости проблемы размещения собственных чисел системы с регулятором путем выбора матрицы является не вырожденность пары матриц , что означает . Если условие управляемости не выполняется, то выбор матрицы не влияет на значение процессов и , и это означает, что система не может быть стабилизирована.





– вектор состояния в новом базисе;

– вектор состояния в старом базисе;

, где

– матрица перехода от старого базиса к новому базису

Представим систему в новом базисе:

; ;

; – уравнение динамики в новом базисе

;

; – матрица динамики в новом базисе

;

. – матрица выхода в новом базисе

Пусть система  является управляемой, опишем систему охваченной ОС в новом базисе:

;

;

;

При ,

.

.

Матрица должна быть выбрана таким образом, чтобы матрица динамики в новом базисе была бы в форме Калмана, при этом матрица входа в новом базисе при была бы единичным вектором столбцом.

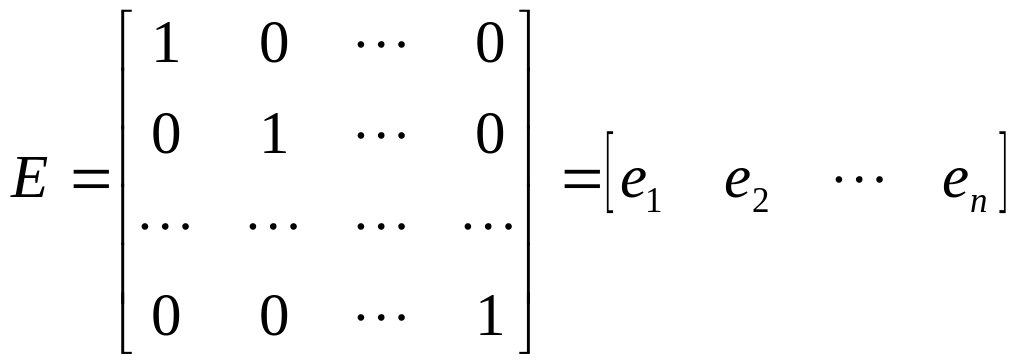
Матрица динамики в форме Калмана может быть записана:

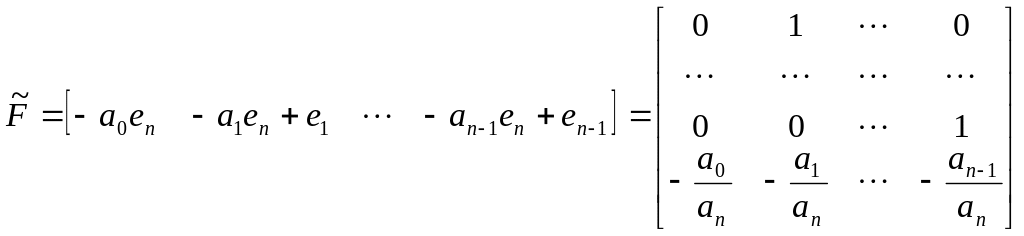, где

– коэффициенты характеристического уравнения .

.

в этом случае будет просто столбец, т.е. .

Не особая матрица со столбцами обеспечивающая представление матрицы динамики в форме Калмана строится рекуррентно по следующим формулам:

Рассмотрим систему с регулятором.

- корни уравнения

;

;

.

Какова связь между и ?

;

Результат показывает, что матрица динамики системы с обратной связью тоже в форме Калмана, а следовательно в последней строке этой матрицы находятся коэффициенты нового характеристического уравнения , которые связаны со старыми следующим образом:

;

– коэффициенты характеристического уравнения матрицы динамики с обратной связью;

; ;

Путем выбора значений можно получить желаемое значение коэффициентов характеристического уравнения матрицы динамики , что соответствует желаемым значениям коэффициентов характеристических чисел, отсюда:

.