Глава 2. Непрерывные функции и функции, имеющие разрывы

2.1. Непрерывность функции

Пусть функция f(x) определена на некотором множестве Е и х₀ – предельная точка множества Е.

Функция f(x) называется непрерывной в точке х₀, если

1. Она определена в точке х₀

2. Существует конечный предел

3. Этот предел равен значению функции в точке х_0.

Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть , где - приращение аргумента и - соответствующее приращение функции.

2.2. Разрывность функции

Итак, если хотя бы одно из трех условий непрерывности не выполняется, функция называется разрывной в точке х₀, а сама точка x₀-точкой разрыва. Если в точке x₀ оба односторонних предела существуют и конечны, то разрыв называется разрывом первого рода. Пусть х₀-точка разрыва первого рода, т.е.

Возможны следующие варианты:

1. f(x₀+0)=f(x₀-0)=L, но либо функция f(x) не определена в точке х₀, либо f(x₀)  L (то есть не выполнено либо первое либо третье условие непрерывности). В этом случае разрыв называется устранимым, так как если доопределить функцию в точке х₀ или переопределить ее, положив f(x₀)=L, функция f(x) станет непрерывной в точке х₀.

2. f(x₀- 0)  f(x₀+0) B этом случае разрыв называется неустранимым.

3. Если же хотя бы один из односторонних пределов f(x₀+0) или f(x₀-0) не существует или бесконечен, то разрыв называется разрывом второго рода. Разрыв второго рода всегда неустранимый.

Если в точке х₀ функции f(x) и g(x) непрерывны, то в этой же точке непрерывными являются и функции

Свойство непрерывности сложной функции

Если функция u=g(x) непрерывна в точке х₀ и функция y=f(u) непрерывна в точке u₀=g(x₀), то сложная функция y=f(g(x)) непрерывна в точке х₀.

Основные элементарные функции непрерывны во всех точках своей области определения.

Таким образом, всякая элементарная функция, т.е. функция, составленная из основных элементарных, с помощью конечного числа алгебраических действий и композиций, является непрерывной во всех точках своей области определения.

Функция непрерывна на отрезке, если она непрерывна во всех точках отрезка.

Рассмотрим на примере, исследуем функцию на непрерывность, найдем точки разрыва и их тип. Построим схематический график функции. Данная функция определена на всей числовой оси.

а) если х < -1, то - многочлен нулевой степени – основная элементарная функция, – следовательно, при x < -1 функция у непрерывна;

б) если –1 < x < 0, то мы имеем композиция степенных функций – элементарная функция, – следовательно, при –1 < x < 0 функция у непрерывна.

в) если х > 0, у=1-х – многочлен 1 степени – непрерывен. «Подозрительными» на разрыв являются только те точки, в которых изменяется аналитическое выражение функции, т.е. точки х=-1, х=0.

• Вычислим односторонние пределы в этих точках.

Для точки х=-1 имеем

Предел слева

Предел справа

Видим, что односторонние пределы функции в точке х = -1 существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.

• Для точки х=0 получаем:

Предел слева

Предел справа

Односторонние пределы существуют и равны между собой. Частное значение функции в точке х=0, у(0)=1, т.к.

С

ледовательно, исследуемая точка является точкой непрерывности.

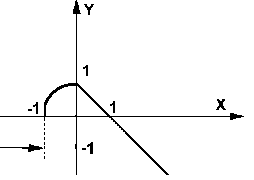
График данной функции:

• на полупрямой (-∞,-1) график представляет собой прямую линию у = -1

• на отрезке [-1,0] график представляет собой часть окружности

• на полупрямой (0, ∞) график представляет собой прямую линию у = 1-х

Вопросы для самопроверки:

1. Какая функция называется непрерывной?

2. Какая функция называется разрывной?

3. Какой разрыв называется устранимым?

4. Какой разрыв называется разрывом 1-ого рода?

5. Какой разрыв называется разрывом 2-го рода?

6. Что Вам известно о непрерывности элементарных функций и основных элементарных функций?