Приложение
Таблица интегралов
(a, b, m, n – постоянные)
I. Интегралы от рациональных функций
1.
,
где n - целое число, не равное 1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
II. Интегралы от иррациональных функций
19.
20.
21.
22.
23.
24.
25.
26.
27.
В формулах 28 – 47 считается, что a > 0, b > 0.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
Примечание:1)Правой части можно придать вид на основании тождества
,
т.е.
41.
42.
43.
44.
или
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
где m, n, r, s – целые
числа, s > 1. Применяется подстановка
,
если
- число целое, и подстановка
,
если
- число целое. В других случаях
интеграл не выражается элементарной
функцией.
III. Интегралы от трансцендентных функций
55.
n
– целое положительное число.
56.
n – целое положительное число.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
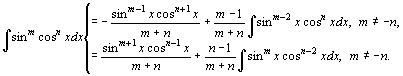
71.
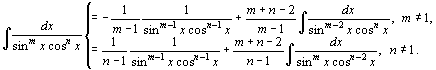
72.
73.
74.
75.
76.
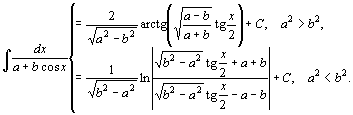
77.
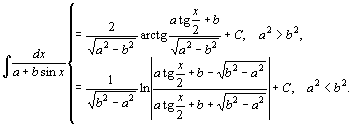
78.
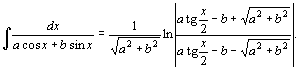
В частности,
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
Рекомендуемая литература:
1. Мордкович А.Г. Алгебра и начало анализа. Учебное пособие. М., 1995
2. Чистяков В.П. Курс теории вероятностей. М., 1996
3. Мацевич И.П. Сборник задач и упражнений по высшей математике. Учебное пособие. Минск, 1996
4. Данко, Попов. Высшая математика в упражнениях и задачах (2-е книги). М., 1996
5. Высшая математика для экономистов. Учебник для ВУЗов. Издание 2 Кремер Н.Ш., Путко Б.А. Издательство: ЮНИТИ 1998
6. Математика в экономике. Учебное пособие Малыхин В.И.Издательство: Инфра-М 2000
7. Дискретная математика. Математика для менеджера в примерах и упражнениях Москинова Г.И. Издательство: Логос 2000
8. Математика в экономике. Учебник в 2-х ч. Солодовников А.С. и др. Финансы и статистика 1999
9. Высшая математика. Учебник для ВУЗов Шипачев В.С. Издательство: Выcшая школа 1998
* Здесь, и в дальнейшем, под с следует понимать как число, так и бесконечность.
1 ) g — ускорение силы тяжести, равное вблизи земной поверхности приблизительно 981 см/сек2, так как (см. п. 2)
2
)
3 ) Когда мы говорим, что два выражения, содержащие знаки неопределенного интеграла, равны друг другу, мы подразумеваем, что эти выражения могут отличаться друг от друга только постоянным слагаемым. Поэтому для того, чтобы доказать, что два такие выражения равны, достаточно убедиться в равенстве их дифференциалов.
4 ) В дальнейшем мы такой проверки проводить не будем. Однако рекомендуем учащимся на первых порах ее проводить с целью самоконтроля.
5 ) Существование обратной функции вытекает из строгой монотонности и непрерывности функции .
6
) Мы должны выбрать в качестве
v какую-либо
функцию, дифференциал которой равен
sin xdx.
Проще всего положить
.
Выбор другой функции имеющей тот же
дифференциал (например,
),
не повлиял бы на результат, а только
несколько усложнил бы выкладки.
7
) Показатели степени
—
натуральные числа, а0 —
коэффициент при старшей степени х
многочлена Р(х).
8
) Заметим, что t
равно половине производной знаменателя:
9
) Рекуррентной формулой для
некоторой последовательности
называется формула, позволяющая выразить
через,
,
если нам известен первый член
последовательности, то с помощью
рекуррентной формулы можно вычислить
любой член последовательности. В данном
случае мы выведем рекуррентную формулу
для последовательности интегралов
10 ) Так как разложение правильной рациональной дроби на сумму простейших всегда возможно, то система уравнений для определения неизвестных коэффициентов разложения не может оказаться противоречивой.
1)
Эта терминология отличается от принятой
в элементарной геометрии, где интервал
называется высотой трапеции, а основаниями
ее называются отрезки параллельных
прямых х = а,
х = b.
В словах, помеченных * ударение следует делать на буквы, выделенные жирным шрифтом.
1) Если Р выражено в килограммах и S в метрах, то А будет выражено в килограммометрах. Если же Р выражено в динах и S в сантиметрах, то А выразится в эргах.
1) Здесь термин «предел» употребляется в смысле, не имеющем отношения к понятию «предел функции».
1) Заметим, что при построении интегральной суммы разность уже не является длиной частичного интервала, а отличается от нее знаком.
1) Мы отметили что доказательство теоремы остается в силе, если подынтегральная функция в отдельных точках обращается в нуль, т. е. в нашем случае функция может в некоторых точках принимать значения т или М. Отметим без доказательства, что в доказываемой теореме знаки неравенств могут перейти в знаки равенств только в том случае, когда функция постоянна.
11 Читатель должен понять, хотя бы на основании простых геометрических соображений, что дифференцировать неравенства, вообще говоря, нельзя.