3.5.2. Несобственные интегралы.

Понятие определенного интеграла было установлено для конечного интервала и непрерывной на нем функции. Данное нами определение интеграла неприменимо, если интервал интегрирования бесконечен или функция в интервале интегрирования имеет точки разрыва. Но довольно часто встречается необходимость распространить определение интеграла на случаи бесконечного интервала интегрирования и разрывной функции.

I. Интеграл с бесконечными пределами. Пусть функция непрерывна для всех значений х, . Тогда мы можем вычислить интеграл от функции , взятый по любому интервалу . Интеграл

тем лучше выражает величину, которую следует принять в качестве интеграла от функции в бесконечном интервале , чем больше . Заставим  неограниченно возрастать. Имеются две возможности: или при имеет предел, или предела не имеет (стремясь к бесконечности или вовсе не стремясь ни к какому пределу, т. е. колеблясь).

Определение. Несобственным интегралом от функции в интервале называется предел интеграла при . Записывают это так:

Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, расходящимся.

Аналогично определяются несобственные интегралы и для других бесконечных интервалов:

где а - любое число, причем  и  изменяются независимо друг от друга.

Рассмотренные интегралы называются интегралами с бесконечными пределами.

Обозначим через первообразную от . Условно запишем:

понимая под символами и пределы, к которым стремится пpи и .

П

Рис.9

редположим, что линия ограничивает трапецию с бесконечным основанием (рис. 9). Если существует несобственный интеграл от функции , взятый вдоль основания трапеции, то естественно считать, что он измеряет площадь этой бесконечной трапеции; в противном случае говорить о площади трапеции нельзя.

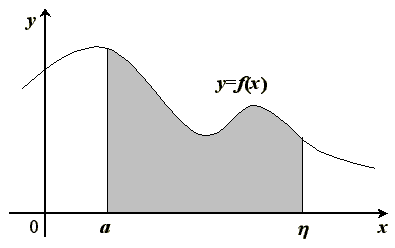
Например, бесконечной трапеции, ограниченной положительной полуосью Ох, прямой и линией , можно приписать площадь, равную ибо

Бесконечной трапеции, ограниченной, например, гиперболой положительной полуосью Ох и прямой , нельзя приписать площади, так как

Примеры. 1) Вычислим интеграл

Имеем:

2) Интеграл расходится, так как величина не стремится к пределу при (колеблется).

3) Если точка М массы т, находящаяся в начале координат, притягивает свободную точку М₁ массы 1, лежащую на расстоянии х от М на оси Ох, то величина Р силы притяжения, как известно, определяется из закона Ньютона

где k – константа,

а работа, произведенная при перемещении М₁ из точки х=r в точку , — из формулы

Знак минус перед интегралом взят потому, что направление силы противоположно направлению движения точки М (по той же причине работа оказалась отрицательной).

Если , то

Если точка M₁ будет перемещаться из бесконечности в точку то сила притяжения произведет уже положительную работу:

Эта работа называется потенциалом силы притяжения материальной точки М при (или в точке .

Укажем два замечательных несобственных интеграла, значения которых находятся специальными методами:

Интересно, что соответствующие неопределенные интегралы не выражаются в элементарных функциях

II. Интеграл от разрывной функции. Если в интервале функция имеет некоторое число точек разрыва первого рода, то определить понятие интеграла для такой функции не представляет никаких затруднений. В самом деле, при этом естественно считать, что интеграл есть просто сумма обыкновенных (собственных) интегралов, взятых по частичным интервалам, на которые разбивается интервал всеми точками разрыва функции.

Обозначим их через будем иметь:

Э

Рис.10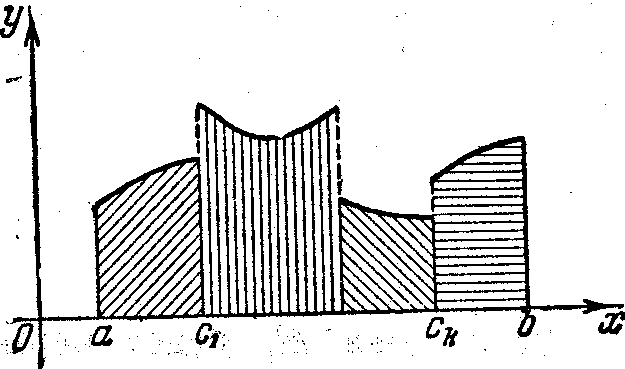

тим самым дается и определение площади криволинейной трапеции, соответствующей функции с конечным числом точек разрыва первого рода в интервале (рис. 10); площадь такой трапеции есть сумма площадей трапеций, опирающихся на частичные интервалы , заключенные между последовательными точками разрыва.

Перейдем к распространению понятия интеграла для функций с бесконечными разрывами.

Пусть функция непрерывна для всех значений х, , а в правом конце интервала претерпевает бесконечный разрыв. Ясно, что обычное определение интеграла здесь теряет свой смысл. Но если взять обыкновенный интеграл

то мы аналогично предыдущему случаю (I) примем, что с уменьшением  все лучше выражает ту величину, которую следует принять в качестве интеграла от функции в интервале . Заставим  произвольным образом стремиться к нулю. Тогда либо имеет предел, либо не имеет (стремясь к бесконечности или вовсе не стремясь ни к какому пределу, т. е. колеблясь).

Определение. Несобственным интегралом от функции , непрерывной при и неограниченной при , называется предел интеграла при

Записывают это так:

Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то расходящимся.

Аналогично, если функция претерпевает бесконечный разрыв только в левом конце х=а интервала , то

Наконец, если функция имеет бесконечный разрыв в какой-нибудь промежуточной точке х=с интервала , то

п

Рис.11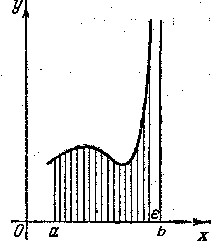

ричем  и  стремятся к нулю произвольно и независимо друг от друга.

Предположим, что линия имеет в точке асимптоту, перпендикулярную к оси Ох; тогда ограниченная ею трапеция будет бесконечной (с бесконечными вы сотами) (рис. 11).

Если существует несобственный интеграл от функции , то считают, что он измеряет площадь этой бесконечной трапеции; в противном случае трапеция площади не имеет.

Например, бесконечной трапеции, ограниченной линией и прямыми можно приписать площадь, равную , ибо

Бесконечной трапеции, ограниченной, например, гиперболой и теми же прямыми нельзя приписать площади, ибо

Пример. Найдем площадь S бесконечного шпиля, ограниченного осью Ох, прямыми и линией Так как функция имеет в интервале точку бесконечного разрыва (х=0), то

Пример.

Здесь подынтегральная функция имеет бесконечный разрыв в точке , лежащей внутри отрезка интегрирования . Поэтому,

Д

Рис. 12

ля графика подынтегральной функции (рис. 12) прямая х=1 является вертикальной асимптотой. Интегралы от этой функции в пределах от -1 до 1-₁ и от 1+₂ до 2 выражают площади криволинейных трапеций аАР и QBb. При и эти трапеции неограниченно простираются вверх и вместе с тем имеют конечные площади, сумма которых равна найденному значению данного несобственного сходящегося интеграла.

Отыскание первообразной по полному дифференциалу. Пусть дано дифференциальное выражение , причем x и y непрерывны вместе со своими частными производными и во всей плоскости Оху или в некоторой односвязной области G.

Функцию двух переменных , полный дифференциал которой равен дифференциальному выражению , назовем первообразной для этого выражения.

Выясним, прежде всего, при каких условиях данное дифференциальное выражение имеет первообразную. Имеет место следующая теорема.

Теорема. Для того чтобы дифференциальное выражение Pdx+Qdy было полным дифференциалом, необходимо и достаточно, чтобы в области G выполнялось условие:

Доказательство. Необходимость. Если есть полный дифференциал, то существует функция , для которой Следовательно,

и

Продифференцировав первое равенство по у, а второе по х, получим

Так как вторые смешанные производные непрерывны (в силу предположенной непрерывности и ), они равны друг другу

Следовательно,

Достаточность примем без доказательства.

Во многих случаях можно найти функцию и по ее полному дифференциалу следующим образом.

Поскольку полный дифференциал равен сумме частных дифференциалов , то интегрируя каждый из них отдельно, найдем два выражения искомой функции u:

где и — неизвестные функции.

Взяв все известные члены из первого выражения, и дописав к ним недостающие члены, зависящие только от у, из второго выражения получим функцию и.

Решение такой задачи легко проверить: если функция и найдена верно, то ее полный дифференциал, найденный по формуле , должен быть тождествен данному полному дифференциалу

Рассмотрим пример. Найти первообразную для дифференциального выражения

Вначале находим частные производные

и убеждаемся, что они тождественно равны и что заданное выражение есть полный дифференциал некоторой функции . Затем найдем эту функцию, интегрируя каждый частный дифференциал Pdx и Qdy отдельно.

а) считая y постоянной;

б) считая х постоянной.

Объединяя эти два выражения — дописав к известным членам первого выражения недостающий член, зависящий только y, из второго выражения, получим одну из первообразных функций, а прибавив к ней произвольную постоянную С, получим общее выражение первообразной функции для заданного полного дифференциала