8. Вопросы для самоконтроля

1. Виды взаимодействия гамма-излучения с веществом?

2. Механизм фотоэлектрического поглощения, зависимость сечения фотоэффекта от энергии фотонов и порядкового номера вещества?

3. Эффект Комптона. Преобразование энрегии гамма квантов при комптоновском рассеянии. Зависимость сечения Комптоновского рассеяния от энергии фотонов и порядкового номера вещества?

4. Преобразование энергии гамма-квантов при эффекте образования пар. Зависимость сечения эффекта образования пар от энергии фотонов и порядкового номера вещества?

5. Ослабление гамма-излучения в веществе. Закономерности и величины характеризующие взаимодействие?

6. Установка для проведения лабораторной работы. Требования к источнику излучения и пучку гамма-квантов, толщине поглотителя, точности измерений?

7. Как экспериментально определить энергию гамма-квантов?

Лабораторная работа № 2 прохождение  - излучения через вещество

Цель и задачи работы. Изучение особенностей взаимодействия -излучения с веществом. Определение с помощью абсорбционного метода граничной энергии -спектра, являющейся одной из важнейших характеристик -излучения радионуклида.

Введение. Отметим, что -частицы - это электроны или позитроны, испускаемые при радиоактивном распаде ядер. -распад представляет собой самопроизвольное превращение нестабильного ядра с зарядом Z в любое ядро изобар с зарядом Z1, происходящее с испусканием (поглощением) легких частиц – лептонов (электронов е^-, нейтрино  и их античастиц - позитронов е⁺ и антинейтрино ).

Изменения в ядрах, происходящие при -распаде, можно представить как превращение одного из нуклонов в нуклон другого сорта по одной из схем:

при ^-, или электронном распаде,

при ⁺, или позитронном распаде,

при Е- захвате (электронный захват).

Лептоны в этих превращениях рождаются или поглощаются подобно фотонам в электромагнитных процессах.

Избыток энергии, содержащийся в -радиоактивном ядре и выделяющийся при распаде, связан с зависимостью внутренней энергии ядра (энергии связи) от соотношения протонов и нейтронов в нем, а также с различием в энергии связи четно-четных (Z и (А-Z) - четное) и нечетно-нечетных (Z и (А-Z) - нечетное) ядер.

Ядра с избытком нейтронов испытывают ^--распад, а с избытком протонов - ⁺-распад и Е-захват. Кроме того, некоторые ядра с четным А испытывают одновременно все три вида -распадов, как, например, ядра ₂₉Cu⁶⁴.

В соответствии с законом сохранения импульса и энергии избыточная энергия распределяется между тремя (двумя в случае Е- захвата) частицами:

Е_= Е_я+Е_е+Е_, (2.1)

г де Е_я и Е_е - кинетические энергии частиц, Е_ - энергия нейтрино. При этом Е_я  0, поскольку . Наличие трех частиц продуктов распада обусловливает важную особенность -распадов – непрерывность энергетического спектра электронов (рис. 2.1(а)). Энергия электронов (и нейтрино) может принимать с различной степенью вероятности значения от нуля до Е_max = Е_. Величина Е_max называется верхней границей -спектра.

Поток электронов можно получить и с помощью ускорителя заряженных частиц, тогда спектр электронов будет практически моноэнергетичным с небольшим разбросом за счет флуктуации параметров ускорительного режима (рис. 2.1 (б)).

Измерение энергетического спектра -частиц является трудной задачей и требует применения магнитных -спектрометров или спектрометров с полупроводниковыми детекторами. Однако, оценка величины верхней границы непрерывного -спектра от радионуклидного источника может быть сделана с достаточно высокой точностью (5%) методом поглощения. Возможны два варианта этого метода: определение толщины полного поглощения (максимального пробега) и метод кратного поглощения по номограммам.

Предварительно рассмотрим кратко процессы взаимодействия электронов с веществом. Электроны являются заряженными частицами, поэтому при взаимодействии движущихся электронов со средой протекают те же процессы, что и при взаимодействии более тяжелых заряженных частиц: ионизация и возбуждение атомов среды, торможение в поле ядер и электронов и упругое рассеяние. Вероятность каждого из эффектов существенно зависит от энергии электронов. Взаимодействие частицы со средой сопровождается потерями энергии вплоть до остановки электрона в веществе. Стоит также отметить, что наличие у электрона малой массы существенно влияет на вероятность протекания указанных процессов.

Ионизация и возбуждение атомов среды. При движении в среде заряженная частица может сталкиваться с атомными электронами и передавать им часть своей энергии. В результате этого электрон атома может перейти на более высоколежащий энергетический уровень (возбуждение), либо покинуть атом (ионизация). Первичный электрон при этом теряет свою энергию, а процесс в целом характеризуется величиной потерь энергии (dE/dx)_ион, измеряемой в единицах .

Ионизационные потери энергии dE – заряженной частицы на пути dx выражается формулой Бете-Блоха

(2.1)

где n - число атомов в 1 см³ среды; I = 13,5Z - средний ионизационный потенциал атомов среды; с - скорость света;  = /c;  - скорость электрона; m_е и Т_е - масса и кинетическая энергия электрона.

Основной физический вывод из формулы (2.1) заключается в том, что потери энергии заряженной частицы на ионизацию атомов среды пропорциональны квадрату заряда ( ) налетающей частицы, плотности электронов среды ( , n – концентрация атомов или ядер среды), некоторой функции от скорости и не зависят от массы налетающей частицы.

(2.3)

Причем потери энергии тем больше, чем меньше скорость заряженной частицы (электрона), т.к. . Таким образом, ионизация и возбуждение преобладают при невысоких энергиях заряженной частицы (до нескольких МэВ)

_{Для электронов формула (2.1) преобразуется в выражение}

(2.2)

Тормозное излучение. При движении заряженной частицы в среде происходит ее взаимодействие с электромагнитным полем ядра и атомных электронов. В результате этого частица испытывает торможение, т.е. двигается с ускорением и, следовательно, имеет возможность испускать электромагнитное излучение. Такое излучение и называется тормозным излучением. Тормозное излучение особенно эффективно генерируется при прохождении быстрых электронов в веществе, поскольку выход данного вида излучения обратнопропорционален массе частицы.

В нерелятивистском случае, когда энергия частицы  потери энергии частицы на тормозное излучение задаются выражением:

(2.4)

где - классический радиус электрона, - постоянная тонкой структуры.

При энергиях заряженной частицы  потери энергии определяются выражением

(2.5)

Таким образом, с ростом энергии заряженной частицы возрастают потери на тормозное излучение, а данный процесс становится преобладающим при энергиях – десятки МэВ и выше.

С ростом энергии электрона изменяется соотношение между ионизационными и радиационными потерями и при некоторой энергии заряженной частицы потери оказываются равными. Такая энергия Е_кр называется критической. Для электронов, движущихся в среде Z с энергией E, соотношение радиационных и ионизационных потерь энергии задается выражением

(2.6)

где Е – энергия электрона в МэВ. Примерные значения E_кр для ряда веществ приведены в табл. 2.1.

Таблица 2.1

Вещество	H (Z=1)	C (Z=6)	Al (Z=13)	Fe (Z=26)	Pb (Z=82)
Eкр, МэВ	800	130	61	31	10

Упругое рассеяние. Кроме неупругого взаимодействия заряженных частиц с атомами, проявляющегося в процессах ионизации и радиационного торможения, в веществе происходит упругое рассеяние электронов и ионов на ядрах атома. Упругое рассеяние происходит без возбуждения ядер и характеризуется перераспределением кинетической энергии взаимодействующих частиц.

Вероятность упругого рассеяния определяется дифференциальным сечением данного процесса, выражаемого формулой Резерфорда

(2.7)

где z₁е, z₂е – заряды взаимодействующих частиц, T – кинетическая энергия налетающей частицы,  - угол рассеяния налетающей частицы. Анализируя (2.7) несложно убедиться, что сечение упругого взаимодействия будет велико при рассеянии на малые углы и небольших значениях кинетической энергии заряженной частицы. Для тяжелых заряженных частиц это будет приводить к тому, что упругое рассеяние будет происходить только в конце пробега частицы в среде.

Таким образом, при попадании высокоэнрегетичной заряженной частицы в среду основные процессы взаимодействия с уменьшением энергии будут преобладать в последовательности: 1) радиационное торможение, 2) ионизация и возбуждение, 3) упругое рассеяние.

При движении заряженной частицы в среде с толщиной, равной, либо больше пробега данной частицы в среде может возникать ситуация, когда последняя испытывает не одно упругое рассеяние, а большое количество последовательных актов рассеяния на малые углы. Такой процесс называется многократным рассеянием и вносит вклад в общие потери энергии заряженной частицы и изменение геометрических факторов пучка частиц (поперечное сечение, разброс длины пути и др.). Основной характеристикой, описывающей многократное рассеяние, является угол многократного рассеяния , который зависит от толщины мишени х как

(2.8)

Многократное рассеяние играет существенную роль при взаимодействии электронов со средой. В силу того, что электроны являются легкими частицами, их энергия при столкновении с ядрами слабо изменяется. Это приводит к тому, что электроны могут испытывать существенно большее число малоугловых актов рассеяния в сравнении с тяжелыми ионами и, соответственно, отклоняться на большой угол , выбывая из первоначального пучка. На качественном уровне влияние многократного рассеяния на траекторию электронов можно выделить три этапа, которые определяются толщиной среды:

1. Первоначально быстрые электроны проходят некоторый отрезок пути прямолинейно, теряя энергию и испытывая незначительное отклонение за счет небольшого числа актов малоуглового упругого рассеяния.

2. С увеличением глубины проникновения в среду энергия электронов уменьшается, а вероятность упругого рассеяния возрастает. На этом этапе реализуется процесс многократного упругого рассеяния. При этом угол многократного рассеяния согласно (2.8)

3. С последующим уменьшением энергии электронов на глубине среды, приближающейся к пробегу электронов в данной среде, число актов упругого рассеяния становится настолько большим, что угловое распределение движения электронов в среде становится диффузным. То есть в конце пробега в веществе направление движения электронов никак не связано с первоначальным направлением движения частиц.

Т аким образом, если тяжелые заряженные частицы, двигаясь в среде, пробегают весь путь до остановки с малым разбросом относительно первоначального направления движения и не выбывают из пучка, то электроны практически сразу начинают изменять направление движения и выбывать из первоначального пучка частиц. Число частиц на различной глубине будет меняться согласно зависимости на рис. 2.2., (а) – для -частиц, (б) – для моноэнергетичных электронов.

Зависимость (а) ослабления потока частиц с ростом глубины пробега (рис. 2.2.) на некоторых участках может подчиняться экспоненциальному закону:

(2.9)

где - начальный поток электронов, - сечение взаимодействия электронов с веществом и -толщина мишени. Произведение

(2.10)

называется коэффициентом ослабления и является характеристикой данного вещества. Единица измерения - = см^-1. Аналогично массовым тормозным потерям вводят и массовый коэффициент ослабления

(2.11)

где  - плотность данного вещества. Единица измерения - .

Характерная толщина мишени, в которой будет выполняться экспоненциальный закон ослабления, рассчитывается с учетом значения характеристик данного вещества, т.е. величины . Взяв обратное значение 1/, получим толщину мишени, где ослабление пучка электронов будет идти согласно (2.9). Необходимо отметить, что для большинства веществ и естественных радионуклидных источников электронов эти значения малы и не превышают 1-2 мм, тогда как пробеги этих электронов существенно больше. В связи с этим кривая ослабления радионуклидов описывается выражением (2.9) на ограниченных участках толщин среды.

Если зависимость (2.9) выполняется, то определить максимальную энергию E_max можно по значению коэффициента ослабления . Соотношение (2.9) можно преобразовать к виду

(2.12)

где - слой половинного ослабления или толщина слоя поглотителя, при прохождении которой первоначальная интенсивность пучка частиц уменьшится вдвое. Вычислив величину можно определить и максимальную энергию бета-частиц. В табл. 2.1 приведены значения слоев половинного ослабления -частиц для алюминия в зависимости от максимальной энергии -спектра.

Таблица 2.1

Слой половинного ослабления [мг/см²] для алюминия в зависимости от граничной энергии -частиц с непрерывным спектром

Емах, МэВ	1/2	Емах, МэВ	1/2	Емах, МэВ	1/2
0,15 0,20 0,30 0,40 0,50 0,60 0,70	2,7 3,8 7,0 11,7 17,5 24 30	0,80 0,90 1,00 1,2 1,4 1,6 1,8	37 45 53 70 87 107 121	2,0 2,2 2,4 2,6 2,8 3,0 3,0	140 150 168 180 195 210 210

В тех ситуациях, когда ослабление излучения не подчиняется соотношениям (2.9, 2.12), пользуются эмпирическими формулами, связывающими пробег R электронов в веществе с их энергией. Эмпирические формулы находят опытным путем, измеряя поглощение фольгами.

Для моноэнергетических электронов с энергией Е_е > 0,6 МэВ пробег в [мг/см²] в алюминии можно определить по формуле

R_Аl = 526 Е_е - 94. (2.13)

Для -частиц с максимальной энергией E_ пробег в алюминии, выраженный в [мг/см²], можно определить по формулам:

при 0,01 МэВ  E_  2,5 МэВ,

R_Аl= 530 E_ -106 при E_ > 2,5 МэВ. (2.14)

Погрешность составляет  5% .

Пробег электронов R_x в любом веществе определяют по известному пробегу в алюминии, используя приближенное соотношение

R_x= R_Al(Z/A)_Al / (Z/A)_x , (2.15)

где Z и A – порядковое и массовое число элементов среды. Помимо приведенных соотношений можно пользоваться известными табличными значениями пробегов электронов с разной энергией в различных веществах.

Кроме эмпирической связи пробега и энергии, устанавливают и аналогичную взаимосвязь максимальной энергии -спектра [МэВ] со слоем половинного ослабления, выраженной в см . Например, для алюминия:

(2.16)

Для других материалов (от водорода до меди) слой половинного ослабления _1/2 [г/см²] можно определить в зависимости от Е_max (МэВ) по эмпирической формуле

(2.17)

Таким образом, для количественных оценок ослабления -излучения в веществе можно использовать:  и _m - линейный и массовый коэффициенты ослабления -излучения в данном веществе, зависящие как от энергии частиц, так и от природы поглощающего материала, R – пробег электронов в данном веществе, _1/2 - слой половинного ослабления излучения.

Для нахождения энергии экспериментально определяют любую из названных величин (, _m, _1/2, R) и по известным теоретическим, либо эмпирическим зависимостям, связывающим их с энергией, определяют Е_ исследуемого радионуклида.

При определении Е_ методом поглощения обычно в качестве поглотителей применяются алюминиевые фольги разной толщины. Для измерения используют, как правило, торцевые газоразрядные счётчики типа МСТ–17, СИ–3Б, СБТ-13 или цилиндрические типа СТС-5 или СТС-6.

Излучатель помещается на таком расстоянии от счётчика, чтобы между ними можно было свободно разместить слой поглотителя, целиком поглощающий данное излучение. Поглотители помещают на диафрагме–кассете из алюминия или латуни. Толщина кассеты должна быть такой, чтобы она пропускала излучение только через отверстие диаметром не более 20 мм. Поглотители следует помещать по возможности ближе к счётчику.

Толщину поглотителей выбирают в зависимости от энергии Е_. Количество поглотителей выбирают из расчета, чтобы на кривой поглощения можно было получить не менее 10-15 экспериментальных точек. Например, при Е_= 0,15-0,20 МэВ толщина поглотителя из Al составляет 0,01 мм, а при Е_ = 0,50-0,70 МэВ она равняется 0,2- 0,3 мм.

Результаты измерений представляют в виде таблиц и графиков. Типичная кривая поглощения однокомпонентного - излучения приведена на рис. 2.3.

Наиболее удобно определять коэффициент ослабления -излучения таких радионуклидов, которые испускают только -излучение, без сопровождающего гамма-излучения. Такими препаратами, например, являются: RaE (²¹⁰Bi) (T_1/2=5 дней), ³²Р (Т_1/2=14,3 дня), ⁸⁹Sr (T_1/2=54,5 дня) другие.

О днако даже при отсутствии ядерного -излучения и характеристического рентгеновского излучения всегда существует некоторый фон, обусловленный характеристическим рентгеновским и тормозным излучением и возникающий при замедлении -частиц в поглотителе (I_ на рис.2.3). Поэтому при определении коэффициента ослабления -излучения нуклидов необходимо определять вклад в результаты измерений тормозного и рентгеновского излучения I_, и при расчётах делать соответствующие поправки.

В случае источников, испускающих наряду с -частицами гамма-кванты, определяется и учитывается доля - и тормозного излучения (I_).

Экспериментальную кривую ослабления -излучения в общем случае строят в полулогарифмическом масштабе, откладывая по оси ординат натуральный логарифм числа сосчитанных импульсов, а по оси абсцисс – полную толщину поглотителя равную

x=x_Al + x_сл + x_воз, (2.18)

где x_Al – толщина алюминиевых поглотителей, x_сл – толщина входного окна торцeвoго счётчика или толщина стенки для цилиндрического счётчика, x_возд – толщина слоя воздуха от препарата до счётчика.

Следует иметь в виду, что слой воздуха толщиной в 1см при нормальных условиях эквивалентен 1,23 мг/см² алюминия.

Кривая ослабления излучения в полулогарифмических координатах имеет вид, представленный на рис.2.4.

1

2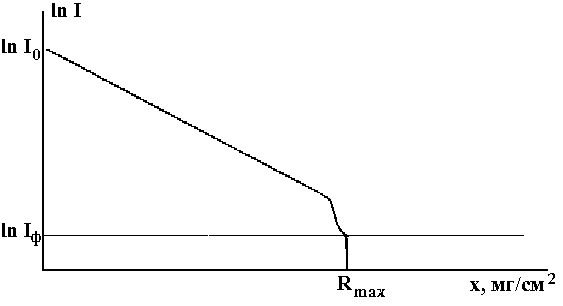

Pис.2.4.Экспериментальная кривая ослабления -излучения

На графике от точки 1 на оси ординат, соответствующей логарифму плотности потока частиц от фона и тормозного излучения, проводят горизонтальную прямую. Из точки 2, где кривая ослабления касается этой прямой, опускают перпендикуляр на ось x. Расстояние от начала координат до этого перпендикуляра – максимальный пробег R_max в данном веществе.

Пробег -частиц в алюминии с максимальной энергией Е_, выраженный в [мг/см²], можно определить по формулам (2.14).

Когда -источник представляет собой смесь двух или более радионуклидов, экспериментальная кривая ослабления имеет вид, представленный на рис.2.5 (кривая 1). Для расшифровки кривой ослабления, обусловленной наличием двух радионуклидов поступают следующим образом: продолжают прямолинейную часть кривой 1 до пересечения с осью ординат (рис.2.5, кривая 2), получают значение в точке x = 0, проводя потенцирование, находят значение , а затем значение откладывают на оси ординат. Далее аналогичным образом выбирая с определенным шагом на кривой 2 значения , , и т.д. определяют значения , , и т.д. строят точки , , и т. д. получая кривую 3.

Рис.2.5. Кривая ослабления интенсивности -излучения источника, состоящего из двух радионуклидов: 1- общая кривая, 2 – кривая ослабления компоненты -излучения с большей энергией, 3 – кривая ослабления компоненты  -излучения с меньшей энергией Е_

Определив тангенс угла наклона прямых 2 и 3, находят величины массовых или линейных коэффициентов ослабления излучения либо пробеги для «жёсткого» и «мягкого» излучателей. Далее используя эмпирические формулы (2.14), связывающие пробеги с энергией -частиц, находят значение максимальной энергии для обоих излучателей. Когда радиоактивный препарат содержит 3 и более -излучателей с различной максимальной энергией - спектра, расшифровка кривых оказывается сложной, хотя она принципиально возможна и описана в специальной литературе.