1.8. Проверка гипотезы о дисперсиях контролируемого параметра

двух больших партий изделий с нормальным законом

распределения по выборкам малого объема (n₁=10; n₂=10)

Гипотеза Н₀: , оценка которых определяется по формулам (14),(15).

Гипотеза Н₁: .

Вид выборки: любая – большая, малая.

Закон распределения: нормальное распределение.

Статистика:1) (основная статистика);

2) .

Статистика 2 часто используется при табулировании.

Закон распределения статистики U:

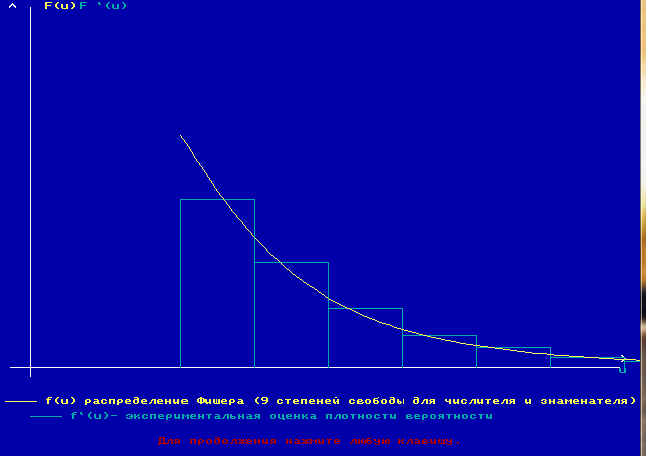
1) F – распределение Фишера с числом степеней свободы числителя и знаменателя

Плотность распределения

(20)

2) F – распределение Фишера с числом степеней свободы числителя (большей дисперсии) _, знаменателя _.

Условие принятия Н₀:

(рис.2)

для числителя,

для знаменателя

МО = 2

Среднее квадратическое отклонение = 1

Значение верхней границы = 4,03

Доверительная вероятность 0,975

Значение верхней границы = 4,03

Доверительная вероятность 0,975

1.9. Проверка гипотезы о дисперсии контролируемого параметра

большой партии изделий с нормальным законом

распределения по выборке малого объема (n₁=10)

Гипотеза Н₀: , оценка определяется формулой (14).

Гипотеза Н₁: .

Вид выборки: любая – большая, малая.

Закон распределения нормальное распределение.

Статистика:

, (21)

где определяется формулой (5).

Закон распределения статистики U– ²–распределение, закон Пирсона с числом степеней свободы k=n₁-1.

Плотность распределения

0  x  . (22)

Условие принятия гипотезы Н₀:

₁² < ² < ₂² . (23)

МО = 2

Среднее квадратическое отклонение = 1

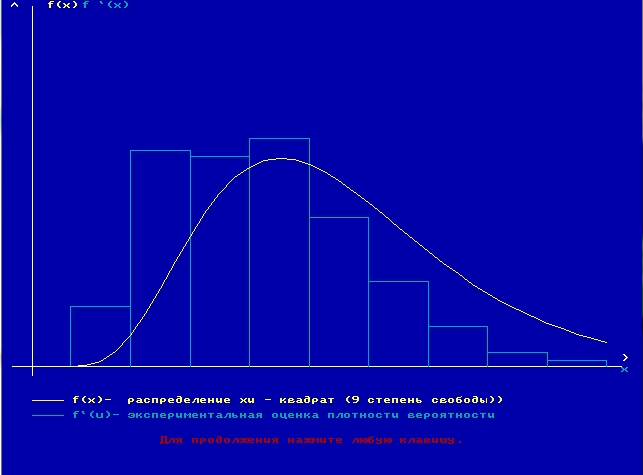
Доверительная вероятность равна 0.95

Значение нижней границы доверительного интервала равно 2.70

Значение верхней границы доверительного интервала равно 19.03

2. Оперативный статистический контроль качества промышленной продукции (многомерный случай)

2.1. Проверка гипотезы о векторе математического ожидания

контролируемых параметров большой партии изделий

с нормальным законом распределения и известной

ковариационной матрицей по выборке малого объема (n₁=40)

Гипотеза Н₀: ,

где - оценка вектора выборочного среднего;

- вектор математического ожидания.

Гипотеза Н₁: .

Вид выборки: любая – большая, малая.

Закон распределения: многомерный нормальный закон распределения. Его плотность распределения записывается в виде

, (26)

где , - определитель матрицы ;

i,j = . (27)

Статистика:

. (28)

Закон распределения статистики U – ²-распределение с числом степеней свободы k=n.

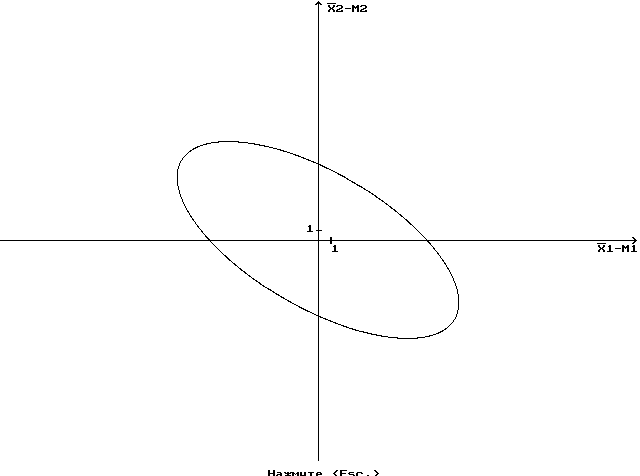
Доверительную область для (28) можно получать в n-мерном пространстве в виде

. (29)

Эта область представляет собой эллипсоид (в двумерном случае – эллипс).

МО X1 = 2, Д = 1

МО X2 = 1, Д = 2

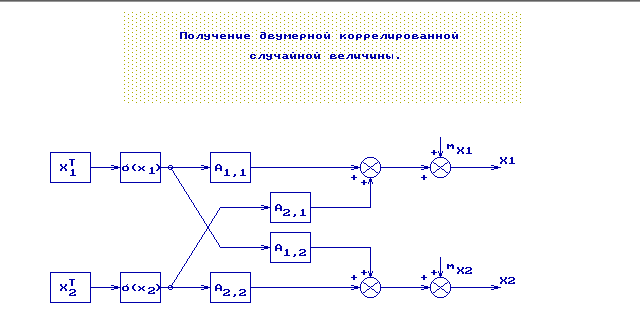
В данном варианте задания корреляционная

матрица R известна и вычисляется c помощью

|Dx1 0|

матрицы A по формуле R=A*| |*A(трансп.)

|0 Dx2|

Пусть матрица A имеет вид:

| 1 -4| Dx1=1.00

A = | | Dx2=2.00

| -5 2|

Используя вышеприведенную формулу найдите матрицу R

Введите R(1,1)

Вы справились с заданием!

Матрица R действительно имеет следующий вид:

| 33.00 -21.00|

R = | |

|-21.00 33.00|