Министерство образования и науки Российской Федерации

РГРТУ

Кафедра АСУ

Отчёт по лабораторной работе № 2 «Оперативный статистический контроль качества промышленной продукции»

Выполнила:

ст. гр. 836

Власова Н. А.

Проверил:

Кабанов А. Н.

Рязань 2012

1. Оперативный статистический контроль качества промышленной продукции (одномерный случай)

1. Проверка гипотезы о математическом ожидании

контролируемого параметра большой партии изделий

с нормальным законом распределения и известной дисперсией

по выборке малого объема (n₁=10)

Гипотеза Н₀: ; .

Гипотеза Н₁: .

Вид выборки: любая – большая, малая.

Закон распределения: нормальный

. (1)

_x² известна.

Статистика – формируемая случайная величина с известным законом распределения:

.

Закон распределения статистики U – нормальный, m_u=0; _u² = 1

Условия принятия Н₀: |U| < |U_kp|

МО = 2

Средне квадратическое отклонение = 1

№ изделия	Значение
1	3,504
2	0,65
3	0,876
4	1,479
5	2,515
6	2,839
7	2,778
8	2,438
9	1,45
10	1,685

┌─────────────┬─────────┬─────────┬───────────────┐

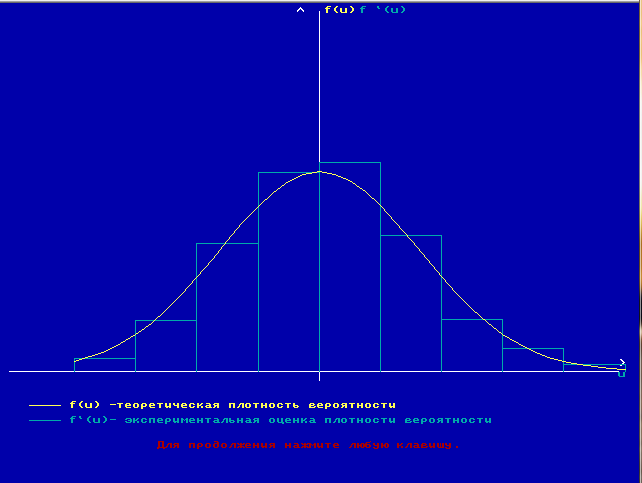
│ интервал │ f`(u) │ f(u)ср. │If(u)ср.-f`(u)I│

├─────────────┼─────────┼─────────┼───────────────┤

│-2.450,-1.838│ 0.026 │ 0.030 │ 0.004 │

│-1.838,-1.226│ 0.101 │ 0.106 │ 0.005 │

│-1.226,-0.614│ 0.255 │ 0.246 │ 0.009 │

│-0.614,-0.002│ 0.399 │ 0.383 │ 0.016 │

│-0.002, 0.609│ 0.418 │ 0.400 │ 0.019 │

│ 0.609, 1.221│ 0.271 │ 0.281 │ 0.009 │

│ 1.221, 1.833│ 0.105 │ 0.132 │ 0.027 │

│ 1.833, 2.445│ 0.046 │ 0.041 │ 0.005 │

│ 2.445, 3.056│ 0.013 │ 0.008 │ 0.005 │

└─────────────┴─────────┴─────────┴───────────────┘

Коэффициент доверия равен 0.95

Значение нижней границы доверительного интервала равно -1.96

Значение верхней границы доверительного интервала равно 1.96

Среднее значение = 1,95

1.2. Проверка гипотезы о математическом ожидании

контролируемого параметра большой партии изделий

с нормальным законом распределения и неизвестной

дисперсией по выборке малого объема (n₁=10).

Гипотеза Н₀: . (5)

Гипотеза Н₁:

Вид выборки: любая – большая, малая.

Закон распределения – (1), где _x² неизвестна.

Статистика:

; (6)

. (7)

Закон распределения статистики U – распределение Стьюдента c n=(n₁-1) степенями свободы [2,стр.31].

Плотность распределения:

, (8)

 t .

Здесь Гамма-функция не имеет аналитического выражения.

Теоретический расчёт:

Практический расчёт:

МО = 2

Среднее квадратическое отклонение = 1

┌─────────────┬─────────┬─────────┬───────────────┐

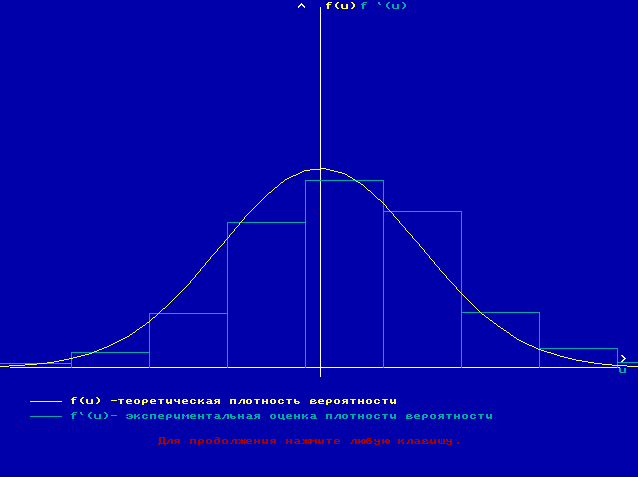
│ интервал │ S`(u) │ S(u)ср. │IS(u)cр.-S`(u)I│

├─────────────┼─────────┼─────────┼───────────────┤

│-3.239,-2.468│ 0.010 │ 0.051 │ 0.040 │

│-2.468,-1.698│ 0.055 │ 0.134 │ 0.080 │

│-1.698,-0.927│ 0.122 │ 0.239 │ 0.117 │

│-0.927,-0.157│ 0.309 │ 0.284 │ 0.025 │

│-0.157, 0.614│ 0.379 │ 0.268 │ 0.111 │

│ 0.614, 1.384│ 0.254 │ 0.183 │ 0.071 │

│ 1.384, 2.155│ 0.117 │ 0.081 │ 0.036 │

│ 2.155, 2.925│ 0.034 │ 0.026 │ 0.007 │

│ 2.925, 3.696│ 0.018 │ 0.007 │ 0.011 │

└─────────────┴─────────┴─────────┴───────────────┘

Коэффициент доверия равен 0.95

Значение нижней границы доверительного интервала равно -2.263

Значение верхней границы доверительного интервала при равно 2.263

Проверка гипотезы о математическом ожидании

контролируемого параметра большой партии изделий

с произвольным законом распределения по выборке

большого объема (n₁=40)

Гипотеза Н₀: ; .

Гипотеза Н₁: .

Вид выборки: большая.

Закон распределения: произвольный.

Статистика – (6),(7).

Закон распределения статистики U нормальный закон, m_u=0; _u² = 1.

Условия принятия Н₀: |U| < |U_kp|.

МО = 2

Среднее квадратическое отклонение = 1

Коэффициент доверия равен 0.95

Значение нижней границы доверительного интервала равно -1.963

Значение верхней границы доверительного интервала при равно 1.963