1.9 Построение диаграммы «энергия-масса»

Диаграмма «энергия-масса» строится путём графического исключения параметра из графиков и , т.е. построение идёт по точкам, полученным при пересечении линий переноса ординат точек соответствующих положений механизма кривых и . График имеет вид замкнутой кривой.

1.10 Определение момента инерции маховика, обеспечивающего вращение звена приведения с заданным коэффициентом неравномерности движения при установившемся режиме работы

Для определения величины момента инерции необходимо провести касательные к графику «энергия-масса» под углами и к оси абсцисс, тангенсы которых определяем по формулам:

, (28)

, (29)

,

,

,

.

Искомый момент инерции найдём из выражения:

(30)

где w₁  угловая скорость электродвигателя ,рад/с

- коэффициент неравномерности вращения кривошипа

Тогда

. (31)

1.11 Определение геометрических размеров маховика

К геометрическим размерам маховика относят диаметр и ширина обода маховика. Из конструктивных соображений примём ширину обода маховика .

Диаметр определим по формуле:

(32)

где  удельная масса материала маховика ( =7850 )

2 Силовой расчёт рычажного механизма с учётом динамических нагрузок

2.1 Построение плана ускорений

Ускорение точки А, находящейся в сложном движении, определяется по формуле

, (33)

где − ускорение точки А в переносном движении, то есть во вращении со звеном 1:

м/с². (34)

− ускорение Кориолиса, определяемое по формуле:

. (35)

Решаем уравнение графически. Для этого из плана ускорений строим вектор мм, соответствующий переносному ускорению точки А. Тогда, масштабный коэффициент равен

, (36)

.

Из полученной точки строим вектор , соответствующий ускорению Кориолиса и равный

мм.

Нормальное ускорение

м/с².

Из полюса плана ускорений строим вектор

мм.

мм.

Определяем величины ускорений, умножая длины соответствующих им векторов на плане на масштабные коэффициенты:

м/с²;

м/с²;

м/с²;

м/с²;

м/с².

2.2 Определение инертных нагрузок звеньев

Силы инерции звеньев определим по формуле:

, (37)

где  масса звена, ;

 ускорение центра тяжести звена,

Силы инерции:

,

Для звена 2 определим расстояние от центров тяжести до точки качания, приняв за точку подвеса точку С.

, (8)

где -момент инерции звена 2, .

.

Тогда

.

Определим положения точки качания. Для этого на построенном в масштабе звене 2 откладываем расстояние от точки . Получаем точку .

Уравнение для силы инерции:

. (9)

Для звена 3 определим расстояние от центров тяжести до точки качания, приняв за точку подвеса точку С.

, (10)

где -момент инерции звена 3, .

.

Тогда

.

Уравнение для силы инерции:

. (11)

Для звена 4 определим расстояние от центров тяжести до точки качания, приняв за точку подвеса точку С.

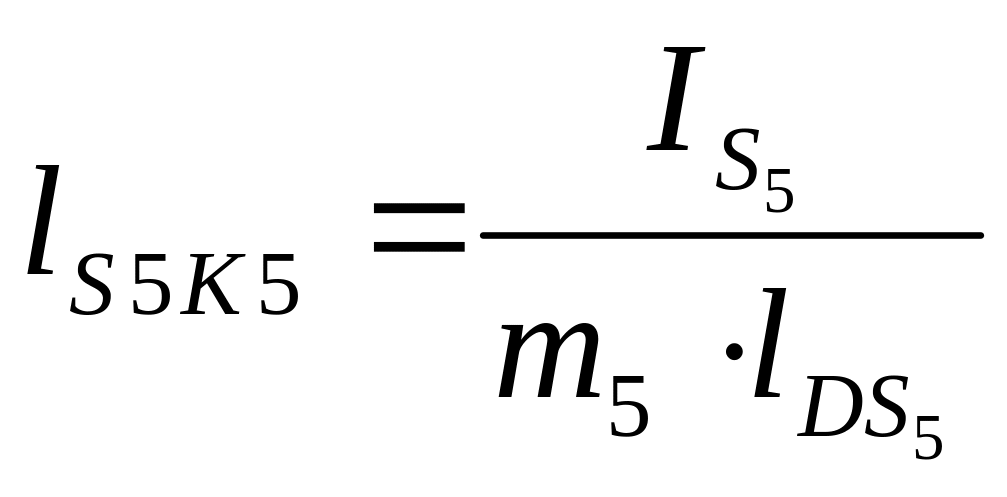, (12)

где -момент инерции звена 2, .

.

Тогда

.

Определим положения точки качания. Для этого на построенном в масштабе звене 2 откладываем расстояние от точки . Получаем точку .

Определим положения точки качания. Для этого на построенном в масштабе звене 4 откладываем расстояние от точки . Получаем точку .

Решим уравнение гр афически. Для этого через точку проводим прямую, параллельную ускорению , а через точку прямую, параллельную ускорению . Через точку пересечения этих прямых проводим прямую, параллельную ускорению и противоположно направленную. Это и будет линия действия силы .