15

М

Исправлено. Окончательный вариант от 14.06.99. Исправлено 15.07.00.

ИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КУРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра вычислительной техники

Работа с датчиками случайных чисел

Методические указания к практической работе №6 по дисциплине "Программирование на языке высокого уровня"

Курск 2000

С оставители: А.Г.Бабанин, И.В.Зотов

УДК 681.3:519.68

Работа с датчиками случайных чисел: Методические указания к практической работе №6 по дисциплине "Программирование на языке высокого уровня" / Курск. гос. техн. ун-т; Сост.: А.Г.Бабанин, И.В.Зотов. Курск, 2000. 16 с.

Рассмотрены принципы построения алгоритмов, использующих датчики случайных чисел. Изложены особенности формирования случайных величин с различными законами распределения средствами языка Паскаль. Даны методические рекомендации по составлению программ, оперирующих со случайными величинами. Приведенные в указаниях примеры ориентированы на программирование в среде Турбо-Паскаль или Borland-Pascal.

Предназначены для студентов специальностей Т 28 и 220100.

Рецензент: канд. техн. наук, доцент Е.А.Бабкин

Ил. 1. Библиогр.: 8 назв.

Текст печатается в авторской редакции

ЛР№020280 от 9.12.96. ПЛД №50-25 от 1.04.97.

Подписано в печать                    . Формат 6084 1/16. Печать офсетная.

Усл. печ. л.       . Уч.-изд. л.        . Тираж 30 экз. Заказ               . Бесплатно.

Курский государственный технический университет.

Подразделение оперативной полиграфии Курского государственного технического университета.

Адрес университета и подразделения оперативной полиграфии:

305040 г.Курск, ул. 50 лет Октября, 94.

Содержание

1. Цель работы 4

2. Методические рекомендации по теоретической части 4

3. Пример решения задачи 6

4. Задачи, выносимые на практические занятия 9

5. Задачи для самостоятельного решения 11

6. Содержание отчета 15

Библиографический список 15

1. Цель работы

Целью данной работы является приобретение практических навыков по разработке алгоритмов и программированию задач с использованием датчиков случайных чисел с различными законами распределения.

2. Методические рекомендации по теоретической части

Величину, которая изменяется случайным образом, называют случайной. Числа х₁,...,х_n, являющиеся значениями случайной величины у, называются случайными числами. При программной реализации этих чисел они называются псевдослучайными, т.к. формируются по определенному правилу. Случайная величина у характеризуется следующими числовыми характеристиками:

• математическое ожидание (среднее):

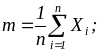
• дисперсия:

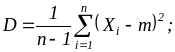
• среднее квадратическое отклонение: ;

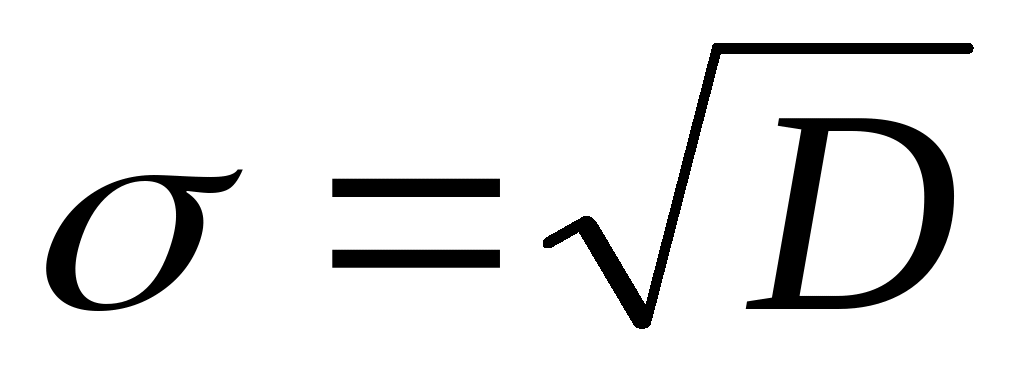• коэффициент асимметрии: ;

• эксцесс: ;

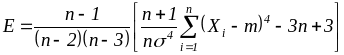• коэффициент вариации: ,

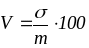где n - число наблюдений случайной величины.

Случайные величины обычно моделируют с помощью преобразований одного или нескольких независимых значений случайной величины Х_R, равномерно распределенной в интервале (0,1). В Паскале для этих целей имеется функция Random [2, c. 130].

Рассмотрим особенности преобразования для случая получения дискретных случайных величин.

Дискретная случайная величина у принимает значения c вероятностями , составляющими дифференциальное распределение вероятностей. При этом интегральная функция распределения (закон распределения)

; ;

; .

Для получения дискретных случайных величин можно использовать метод обратной функции. Если X_R - равномерно распределенная на интервале (0,1) случайная величина, то некоторая случайная величина у получается с помощью преобразования , где - функция, обратная .

Случайную величину у с произвольной плотностью распределения можно, таким образом, найти по следующей методике:

1) смоделировать случайную величину Х_R ;

2) положить Х_R = F(y) ;

3) решить уравнение относительно у.

Так как интеграл в последнем уравнении аналитически берется редко, вычисление случайной величины у можно свести к выполнению следующих действий:

если Х_R1<p₁ , то у=у₁, иначе,

если Х_R1<p₁+p₂ , то у=у₂, иначе,

. . . . . .

если , то у=у_m, иначе,

. . . . . .

Рассмотрим формулы получения случайных величин для некоторых законов распределения вероятностей.

1. Равномерный закон распределения на интервале (а,b), заданный плотностью при моделируется как .

2. Нормальный закон распределения можно моделировать как либо по методу полярных координат: , . Здесь предполагается, что m=0 и D=1.

3. Случайная величина с нормальным законом распределения и произвольным математическим ожиданием m и дисперсией моделируется , где у - нормальная случайная величина с m=0 и D=1.

4. Случайная величина с экспоненциальным распределением и функцией плотности получается как .

5. Дифференциальная функция распределения Хи-квадрат определяется одним параметром k- числом степеней свободы и равна

где - гамма-функция. Случайная величина y, распределенная по этому закону , где Х_N - нормально распределенная случайная величина из n.2.

6. Геометрическое распределение P(x)=p(1-p)^x также зависит от одного параметра p и случайная величина y определяется в этом случае по формуле:

.

Другие законы распределения и методы их моделирования можно найти в учебной литературе, указанной ниже.

В целях наглядности для генерируемых распределений вероятностей часто строят гистограммы. Если случайные числа заданы в диапазоне [a,b] и имеется n случайных чисел, то выбирается N классов случайных чисел и вычисляется длина каждого класса . Затем определяется количество чисел, попадающих в каждый класс. Тогда гистограмма - это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат l, а высоты пропорциональны числу чисел, попавших в соответствующий класс.

Для успешного составления программ с использованием датчиков случайных чисел необходимо изучить следующие вопросы:

1. Способы получения случайных чисел с различными законами распределения.

2. Способы использования в программах обращений к функциям и подпрограммам для получения псевдослучайных чисел с различными законами распределения.

3. Способы использования случайных чисел для моделирования.