5. Восьмеричная и шестнадцатеричная системы счисления

Пример 2.5.1 Запишите в шестнадцатеричной и восьмеричной системах счисления первое число: 2023₁₀ (в двоичной системе счисления оно выглядит как 11 111 100 111₂).

Решение. Для того чтобы целое двоичное число записать в системе счисления с основанием 2ⁿ нужно выполнить следующие действия:

1) число разбить справа налево на группы цифр по n цифр в каждой;

2) если в крайней левой группе окажется меньше разрядов, то дополнить её нулями слева до нужного числа разрядов;

3) рассматривая каждую группу как n-разрядное двоичное число, заменить её соответствующей цифрой в системе счисления с основанием 2ⁿ, используя таблицу 3.

Таблица 3 – Представление чисел в различных системах счисления

Десятичная	Двоичная	Восьмеричная	Двоичная (триады)	Шестнадцатеричная	Двоичная (тетрады)
0	0	0	000	0	0000
1	1	1	001	1	0001
2	10	2	010	2	0010
3	11	3	011	3	0011
4	100	4	100	4	0100
5	101	5	101	5	0101
6	110	6	110	6	0110
7	111	7	111	7	0111
8	1 000	10	001 000	8	1000
9	1 001	11	001 001	9	1001
10	1 010	12	001 010	A	1010
11	1011	13	001 011	B	1011
12	1100	14	001 100	C	1100
Окончание таблицы 3
Десятичная	Двоичная	Восьмеричная	Двоичная (триады)	Шестнадцатеричная	Двоичная (тетрады)
13	1101	15	001 101	D	1101
14	1110	16	001 110	E	1110
15	1111	17	001 111	F	1111
16	10000	20	010 000	10 000	0001 0000

Воспользуемся таблицей 3 для перевода данного число в шестнадцатеричную систему счисления.

Исходное число			Разделяем на тетрады				Результат
11111101112	→		0011	1111	0111	→	3F716
			3	F	7
Исходное число			Разделяем на тетрады				Результат
1 111 110 1112	→	001	111	110	111	→	17678
		1	7	6	7

Пример 2.5.2 Запишите в шестнадцатеричной и восьмеричной системах счисления четвертое число: 1964₁₀ (двоичная запись числа: 11110101100₂).

Решение. Перевод из десятичной системы в m-ричную систему счисления производится аналогично переводу в двоичную систему путем целочисленного деления десятичного числа на основание системы m до тех пор, пока частное не станет меньше основания. Так, перевод исходного числа в шестнадцатеричную и восьмеричную систему осуществляется следующим образом:

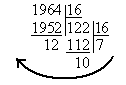1964₁₀=7AC₁₆ 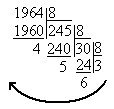1964₁₀=3654₈

7AC₁₆ = 7·16² + 10·16¹ + 12·16⁰ = 7·256 + 160 + 12 = 1792 + 160 + 12 = 1964₁₀

3654₈ = 3·8³ + 6·8² + 5·8¹ + 4·8⁰ = 3·512 + 6·64 + 5·8 + 4 = 1536 + 384 + 40 + 4 = 1964₁₀

Пример 2.5.3 Выполнить обратное преобразование (из восьмеричной и шестнадцатеричной системы счисления в двоичную) исходного заданного числа: 1964 или 7AC₁₆ и 3654₈

Решение. Достаточно заменить каждую из восьмеричных или шестнадцатеричных цифр на три или четыре двоичные цифры в соответствии с приведенной выше таблицей.

7AC₁₆ = 0111 1010 1100₂

3654₈ = 011 110 101 100₂