Контрольные вопросы

1. Изопроцессы. Их уравнения и графики.

2. Первое начало термодинамики для изопроцессов.

3. Адиабатический процесс. Уравнение Пуассона.

4. Теплоёмкость. Теплоёмкости идеального газа и .

5. Коэффициент Пуассона, уравнение Майера.

6. Метод Клемана и Дезорма, определения коэффициента Пуассона.

7. Обработка результатов измерений и расчет погрешности определе­- ния .

Лабораторная работа 2–4 определение удельной теплоёмкости воздуха при постоянном давлении методом протока

Цель работы: определение удельной теплоёмкости воздуха при постоянном давлении.

Приборы и принадлежности: лабораторный модуль, приборный модуль.

Краткая теория

Удельная теплоёмкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:

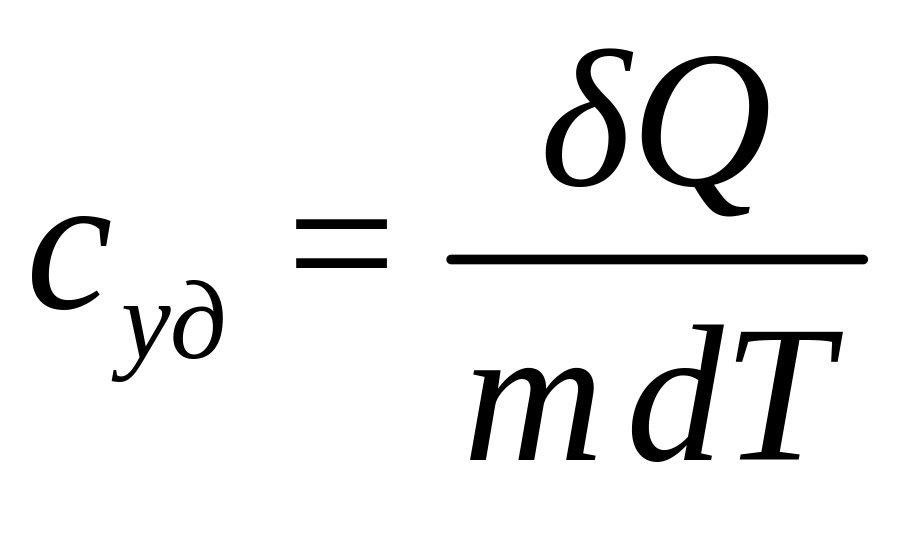^. (1)

Единица удельной теплоёмкости – джоуль на килограмм-кельвин (Дж/кг·К).

В теории газов чаще используют молярную теплоемкость. Молярная теплоёмкость – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:

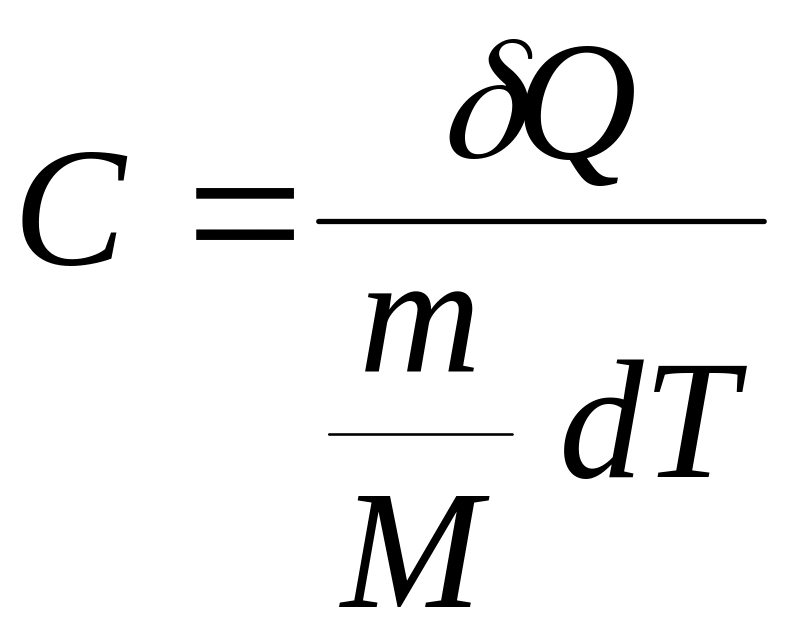. (2)

Единица молярной теплоёмкости − джоуль на моль-кельвин (Дж/моль·К).

Между удельной и молярной теплоемкостями существует связь:

^. (3)

Теплоемкость газов зависит от условий, при которых происходит нагревание газа. Поэтому различают разные теплоемкости, соответствующие разным процессам нагревания.

Наибольшее практическое значение имеют теплоемкость газа при постоянном объеме (газ нагревают так, что его объём не меняется в процессе нагрева) и теплоемкость при постоянном давлении (газу передают тепло так, что его давление остается постоянным).

Из молекулярно-кинетической теории для этих теплоёмкостей следует:

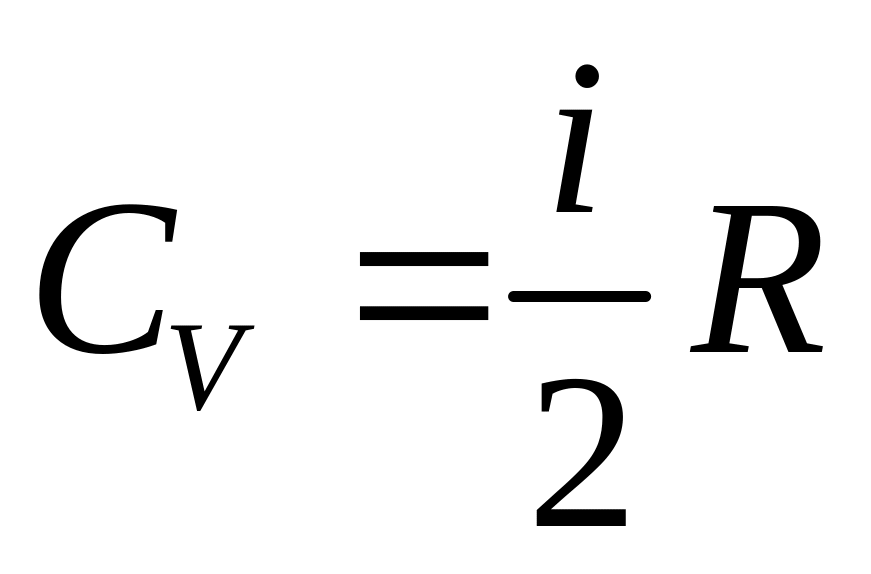, ^, (4)

где число степеней свободы молекулы; универсальная газовая постоянная.

В данной лабораторной работе определяется удельная теплоёмкость воздуха при постоянном давлении . Для этого используется метод протока.

В лабораторной установке воздух прокачивается компрессором через трубку с размещенным в ней нагревателем (спиралью). Трубка и нагреватель находятся в теплоизолирующей оболочке – сосуде Дьюара. Протекая по трубке, газ заметно нагревается и расширяется, но практически не изменяет своего давления, именно поэтому измеряемую теплоёмкость можно считать теплоёмкостью при постоянном давлении.

Примечание. Масса воздуха m₁, проходящая через поперечное сечение трубки в единицу времени, слабо зависит от температуры, и её можно считать константой.

Количество теплоты, которое получает воздух от нагревателя в единицу времени, определяется мощностью, выделяемой нагревателем:

, (5)

где напряжение на спирали нагревателя, а ток, протекающий по ней.

Меняя напряжение, можно изменять количество теплоты, получаемого воздухом в единицу времени. При этом будет меняться разность температур воздуха на входе и выходе трубки.

Примечание. Часть тепла, полученного от нагревателя, воздух отдаёт теплоизолирующей оболочке. Величина этих потерь зависит от температуры воздуха, однако в первом приближении эти потери в данной лабораторной установке можно считать постоянной величиной.

Температура воздуха на входе трубки равна температуре воздуха в лаборатории. Температура воздуха на выходе из трубки отличается от комнатной на некоторую величину (её в данной лабораторной установке определяют с помощью термопары).

Если произвести измерение разности температур Т₁ и Т₂ при двух различных значениях напряжения на концах спирали, то искомую удельную теплоёмкость воздуха при постоянном давлении можно найти по формуле:

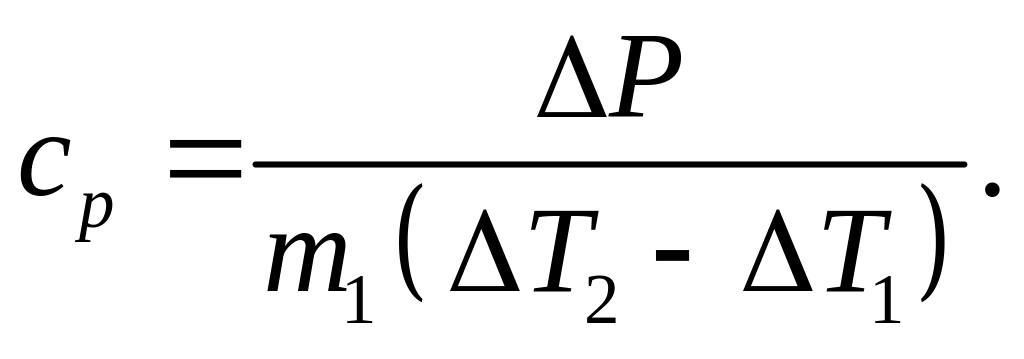(6)

где изменение мощности спирали при изменении напряжения на её концах.

Значения тока , который протекает по спирали при разных U, определяют, используя балластное сопротивление R_Б, включенное последовательно со спиралью. Для этого измеряют падение напряжения U_б на этом сопротивлении и вычисляют ток по закону Ома:

^. (7)

Разность температур на концах трубки и термоЭДС термопары, применяемой в данной лабораторной установке, в используемом интервале температур линейно связаны:

(8)

где размерность милливольт.

Массу воздуха m₁, проходящего в единицу времени через поперечное сечение трубки с достаточной степенью точности можно вычислить по формуле:

, (9)

где разность (в метрах) высот воды в правом и левом коленах манометра, установленного на лабораторном модуле.