Лабораторная работа 2–3 определение отношения для воздуха

Цель работы: ознакомление с методом Клемана и Дезорма и определение отношения для воздуха.

Приборы и принадлежности: лабораторный модуль приборный модуль.

Краткая теория

Теплоемкость газов зависит от условий, при которых происходит их нагревание. Различают теплоемкости, соответствующие разным процессам нагревания. Наибольшее практическое значение имеют молярные теплоемкости газа при постоянном объеме и при постоянном давлении .

Отношение этих теплоёмкостей является важным параметром. В частности, оно входит в уравнение адиабаты (уравнение Пуассона):

, (1)

показывающее как связаны давление и объём газа в процессах, происходящих с газом без теплообмена с окружающей средой. Из молекулярно-кинетической теории идеального газа следует, что для воздуха параметр 1,4.

В данной лабораторной работе определяется значение показателя адиабаты  (её называют постоянной, или коэффициентом Пуассона) для воздуха методом, предложенным и осуществлённым в 1819 г. Клеманом и Дезормом.

Баллон вместимостью несколько литров (рис. 1) наполняется исследуемым газом при атмосферном давлении Р₀. С помощью насоса в баллон дополнительно накачивается небольшая порция того же газа, затем кран К₁ закрывается. Через некоторое время температура газа в баллоне становится равной температуре окружающей среды Т₀. При этом давление газа будет отличаться от атмосферного: Р₁ = Р₀ + Р₁.

Разность давлений (перепад давлений) внутри и вне сосуда определяется с помощью водяного манометра по формуле Паскаля для гидростатического давления:

, (2)

где плотность воды; ускорение свободного падения; разность уровней воды в изогнутой трубке манометра (см. рис. 1).

Затем на короткое время открывают кран К₂. Газ, находившийся в баллоне, расширяется, при этом часть его выходит из баллона. Давление в баллоне становится атмосферным, а температура понижается до некоторого значения Т. Охлаждение связано с тем, что газ, расширяясь во внешнюю среду, совершает работу за счёт своей внутренней энергии. Из-за кратковременности процесса расширения он проходит без теплообмена с окружающей средой, т. е. адиабатически.

Спустя некоторое время после закрытия крана К₂ температура газа опять сравнивается с температурой окружающего воздуха. Поскольку этот процесс происходит изохорно, давление в баллоне повысится: Р₂ = Р₀ + Р₂. Величина Р₂ также определяется с помощью манометра.

Измеренные значения перепадов давлений Р₁ и Р₂ позволяют вычислить величину коэффициента Пуассона для воздуха.

М

28

ысленно выделим внутри баллона произвольную замкнутую поверхность (рис. 1, пунктирная линия). Она играет роль оболочки, в которую заключена некоторая порция газа. В различных процессах газ, заключенный в эту «оболочку», расширяясь и сжимаясь, будет совершать работу против давления окружающего газа и обмениваться с ним теплом. Эти процессы можно рассматривать как квазистатические, так как энергия возникающего макроскопического движения газа невелика. 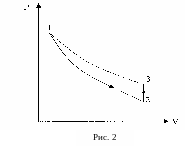В течение одного цикла измерений выделенная порция газа проходит через три состояния, термодинамические параметры которых имеют следующие значения:

1 состояние: Р₁ Т₀ V₁

2 состояние: Р₀ Т V₂

3 состояние: Р₂ Т₀ V₂

Эти состояния и переходы между ними показаны в координатах P – V на рис. 2. Процесс 1–2 происходит адиабатически, процесс 2–3 – изохорно. Состояния 1 и 3 лежат на одной изотерме (пунктирная линия). Это означает, что для параметров перечисленных состояний справедливы уравнения:

и

из которых следует:

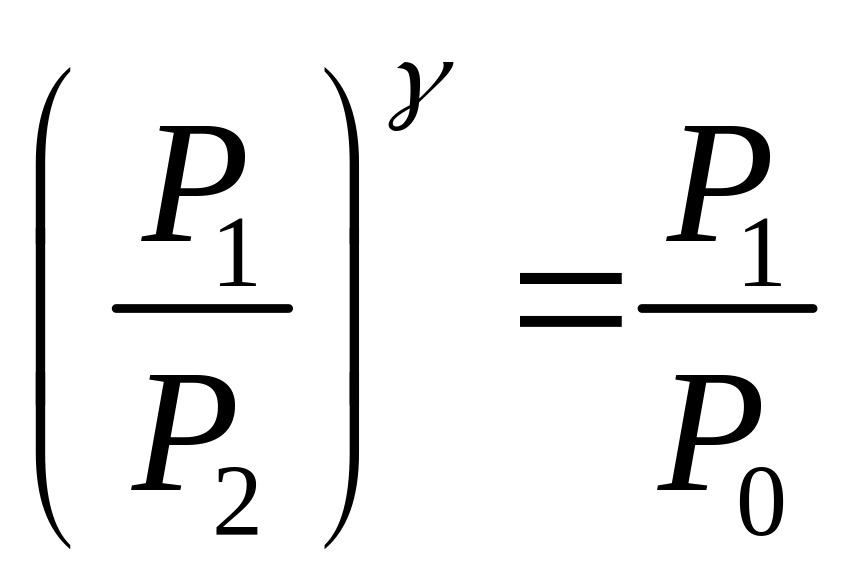. (3)

Логарифмируя (3), получаем:

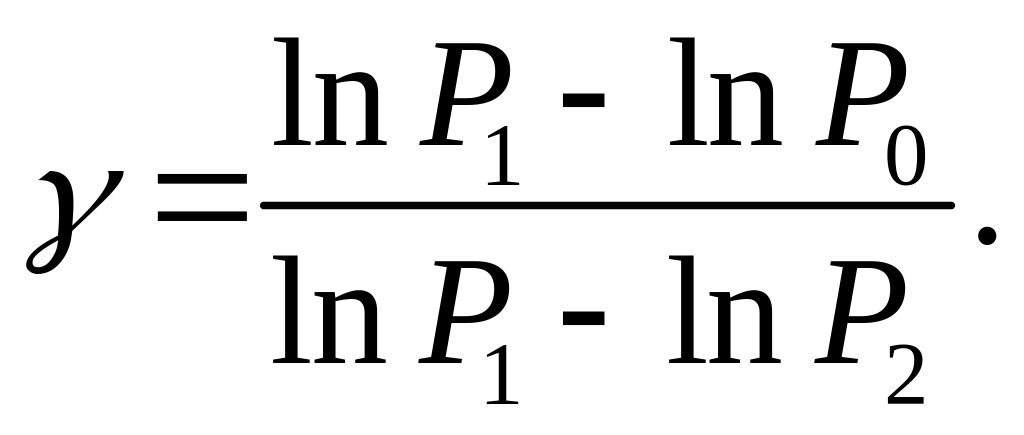(4)

Зная атмосферное давление, пользуясь (4) можно найти искомую постоянную Пуассона. Однако без измерения Р₀ можно обойтись. Дело в том, что в опыте Клемана и Дезорма давления Р₁ и Р₂ мало отличаются от Р₀, т. е. выполняются неравенства: и . Причём, согласно (2):

,

а

.

Если принять во внимание, что при для функции справедливо выражение:

,

из (4) нетрудно получить приближенную формулу для расчёта коэффициента Пуассона:

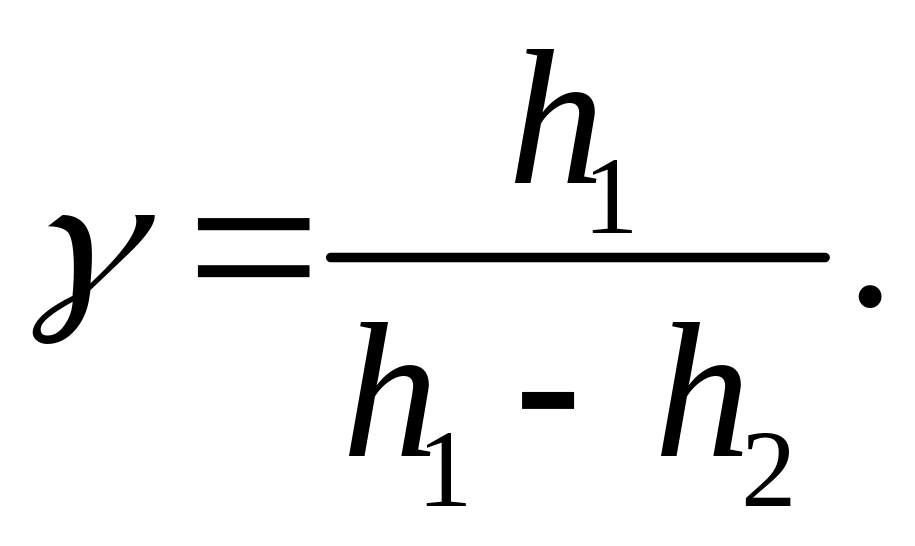(5)

Отметим, что постоянная Пуассона при учёте уравнения Майера позволяет находить молярные теплоёмкости исследуемого газа:

(6)