17. Затухающие колебания. Логарифмический декремент затухания.

В реальных условиях на тело со стороны окружающей среды действуют силы трения, препятствующие движению. На преодоление сил трения расходуется энергия. Вследствие этого, энергия колеблющегося тела уменьшается и, следовательно, уменьшается амплитуда колебаний, т.е. колебания становятся затухающими. Запишем второй закон Ньютона для реальных условий:

. Так как все силы действуют вдоль одной линии, то в скалярном виде уравнение движения будет иметь вид: . При небольших скоростях движения сила трения пропорциональна скорости и направлена противоположно ей, поэтому , где r – коэффициент трения. Тогда второй закон Ньютона запишется

перенесем все члены уравнения в левую часть и разделим на m:

Получили дифференциальное уравнение затухающих

колебаний, общее решение которого будет иметь следующий

вид:

где w- круговая частота затухающих колебаний:

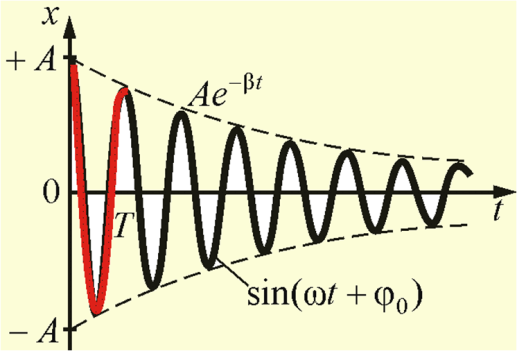
Выражение является уравнением затухающих колебаний. Оно отличается от чисто гармонического колебания тем, что амплитуда колебания с течением времени уменьшается. Пунктиром на этом рисунке изображена зависимость амплитуды от времени.

На практике степень затухания характеризуется логарифмическим декрементом затухания l. l – это натуральный логарифм отношения двух амплитуд затухающего колебания, отличающихся на один период:

Физический смысл логарифмического декремента затухания заключается в том, что это величина, обратная числу колебаний, после которых амплитуда уменьшается в е раз:

Где - это число колебаний, которое успевает совершить колеблющееся тело за время, в течение которого амплитуда колебаний уменьшается в е раз.

18. Вынужденные колебания. Резонанс.

В ынужденными называются колебания, которые возникают в системе под действием внешней силы, изменяющейся по периодическому закону, например,

. F₀ - амплитуда вынуждающей силы, W - ее круговая частота. Тогда второй закон Ньютона запишется: Пусть сила трения равна нулю F_тр = 0, тогда

Разделив это уравнение на m, и перенося члены с х в левую часть, получим дифференциальное уравнение:

Решение этого уравнения имеет вид . При действии вынуждающей силы тело будет колебаться с частотой вынуждающей силы. Значение амплитуды в уравнении определяется следующим образом:

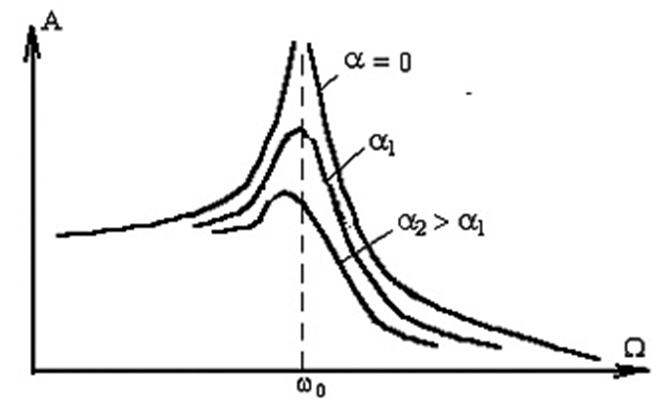
Видно, что амплитуда колебаний зависит не только от амплитуды вынуждающей силы, но и от разности квадратов собственной частоты и частоты вынуждающей силы. Графически эта зависимость представлена на рис. 11. Отдельные кривые на графике соответствуют различным значениям параметра a (коэффициента затухания), чем меньше a, тем выше и правее лежит максимум данной кривой. При W = w₀ амплитуда вынужденного колебания стремится к бесконечности. Явление резкого возрастания амплитуды вынужденых колебаний при совпадении частоты вынуждающей силы с собственной частотой системы называется резонансом.