13. Полная энергия собственных колебаний.

В простых гармонических колебаниях происходит непрерывный переход потенциальной энергии в кинетическую энергию, и обратно. Полная энергия колеблющейся системы сохраняется, если в системе отсутствуют силы трения. Выясним, как изменяется со временем кинетическая Е_k и потенциальная U энергия гармонического колебания. Кинетическая энергия равна

. Потенциальная энергия выражается формулой

. Выражения для полной энергии:

Е ~ А²

14. Сложение колебаний, направленных вдоль одной прямой.

В озможны случаи, когда на тело действуют несколько упругих сил. Каждая из этих сил заставляет тело совершать гармоническое колебание. При одновременном воздействии этих сил тело одновременно будет участвовать во всех этих движениях. Примером может служить барабанная перепонка, одновременно воспринимающая множество звуковых колебаний. В этом случае, чтобы найти результирующее движение, необходимо сложить колебания. Пусть тело одновременно участвует в двух гармонических колебаниях с одинаковыми частотами, но разными амплитудами и начальными фазами, направленных вдоль одной прямой:

Результирующее колебание может быть изображено вектором амплитуды

А = А₁ + А₂ и вращающимся вокруг т. О с той же угловой ω.Для определения результирующего смещения применяется векторный метод сложения колебаний.

Ox – опорная прямая A₁, А₂ и φ₁, φ₂ – амплитуда и фаза 1-го и 2-го колебания в момент времени t=0. Так как векторы вращаются с одинаковой угловой скоростью, то и их результирующий вектор А будет вращаться с той же угловой скоростью, то есть, результирующее движение также будет гармоническим с круговой частотой w.

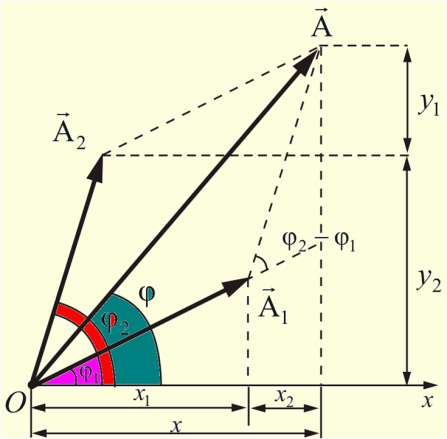
Результирующее колебание определяется уравнением вида . Из рис. 4 и теоремы косинусов видно, что

Начальная фаза определяется из соотношения

.

15. Ч астные случаи.

1 . Разность фаз равна нулю или четному числу π, то есть , где:

Тогда колебания синфазны

2. Разность фаз равна нечетному числу π, то есть

колебания в противофазе. А₁ = А₂, фазы противоположны. Результирующее колебание = 0 (min)

3. Разность фаз изменяется во времени произвольным образом

Это негармонические колебания

16. Биения .

О собый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте . Если амплитуды двух гармонических колебаний, направленных вдоль одной прямой, одинаковы, а частоты мало отличаются друг от друга, то в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой.

ω = ω +Δω. Эти колебания называют биениями..

,

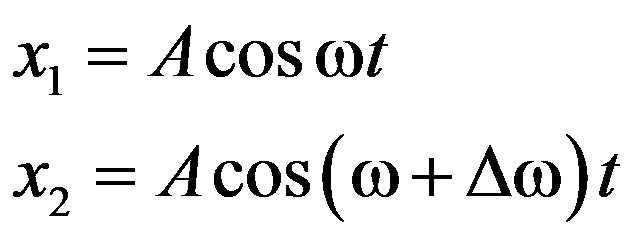
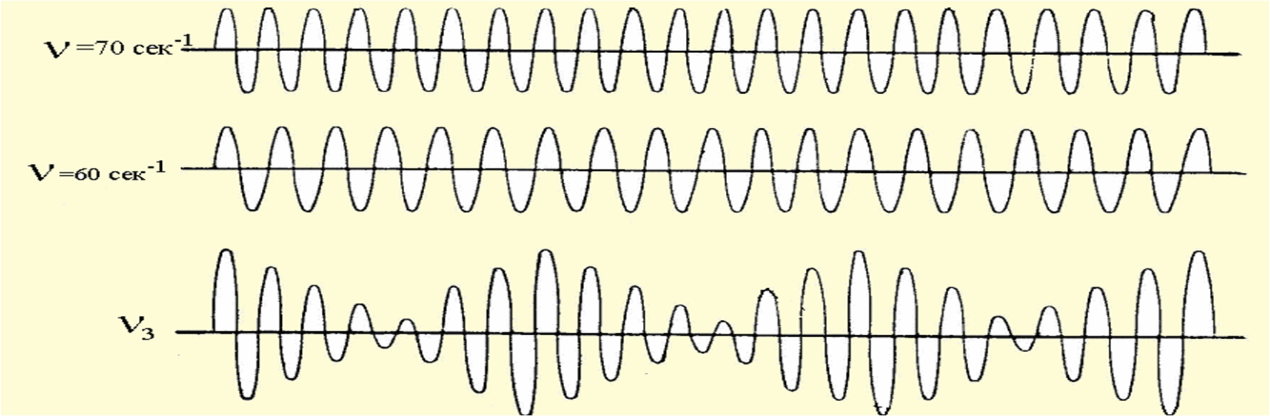
Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д.