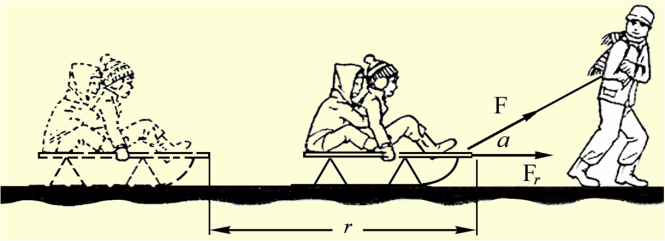
8. Работа и мощность.

В физике работа имеет строго определённый смысл. Если мы прикладываем к телу силу и перемещаем его на определённое расстояние, то говорят, что совершается работа. Работа, совершаемая постоянной (как по величине, так и по направлению) силой при перемещении тела определяется , где F - постоянная сила, S - результирующее перемещение, ά - угол между направлениями силы и перемещения.

Р абота – это скалярная величина. Если вектор силы и направление перемещения образуют острый угол ( ), то работу считают положительной. Если угол – тупой( ), то работа отрицательна. При работа равна нулю, т.е. сила, действующая перпендикулярно к перемещению тела, работы не производит. Во многих случаях в процессе движения сила меняется по величине или направлению. Допустим, материальная точка движется по траектории приэтом в разных точках траектории сила, действующая на материальную точку различна понаправлению и величине. Если сила не постоянна, то производимое при движении приращение работы на бесконечно малом отрезке пути dr запишется в виде dA = (F,dr).

Полная работа, производимая при перемещении тела из точки C в точку D, равна

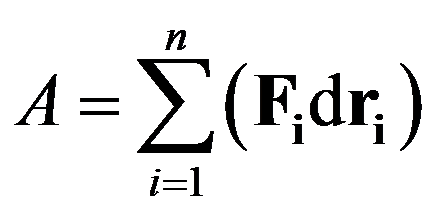
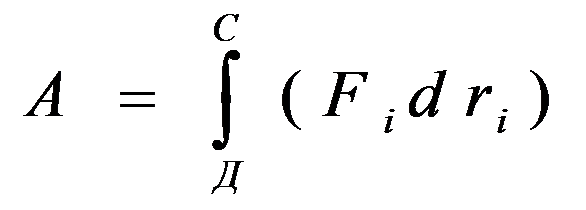
Единицей измерения работы является джоуль (Дж). Джоуль представляет собой, работу движущей силы в 1 ньютон на отрезке пути в 1 метр: 1Дж = 1Н * 1м. Для характеристики скорости выполнения работы вводят понятие мощности.

Мощность – это физическая величина численно равная работе, совершенной в единицу времени:

Единица мощности – 1ватт (Вт). 1Вт = 1 Дж/с.

9. Понятие энергии. Кинетическая энергия. Связь работы с изменением кинетической энергии тела.

З апасенная работоспособность тела в механике называется энергией. Изменение энергии системы тел всегда оценивается работой, совершенной внешними силами, приложенными к системе: . Энергия измеряется в тех же единицах, что и работа. Когда работа внешних сил положительна (A>0), то энергия системы возрастает и, наоборот, если работа внешних сил отрицательна (система

совершает работу), то энергия системы убывает. Следовательно, система может совершать работу только за счет изменения своей энергии. Различают два вида механической энергии:

Кинетическая энергия – это энергия, которой обладают движущиеся тела;

Потенциальная энергия - это энергия, которая характеризует взаимодействие тел или отдельных частей тела.

Кинетическая энергия.

Движущееся тело может совершить работу над другим телом, с которым оно соударяется (движущийся молоток забивает гвоздь; летящее пушечное ядро разбивает стену). В любом из этих случаев движущееся тело действует с определенной силой на второе тело и перемещает его на некоторое расстояние, т.е.

совершает работу. Поэтому мы говорим, что движущееся тело обладает кинетической энергией. Для того чтобы, получить количественное выражение для кинетической энергии, вычислим работу, которую может совершить движущееся тело в частном случае одномерного движения. Пусть тело массой m₁ движется вдоль прямой со скоростью и ударяет второе тело. Поскольку на второе тело подействует сила, то второе тело изменит скорость своего движения, т.е.

первое тело совершит работу, перемещая второе тело. Найдем выражение этой работы

,так как сила F изменяет скорость движения второго тела, то она

с ообщает ему ускорение. Поэтому, согласно 2-му закону Ньютона , подставим это значение силы в выражение для работы:

Тогда выражение для работы можно записать следующим образом:

В еличина называется кинетической энергией. Таким образом, работа численно равна изменению кинетической энергии тела, т.е. работа, совершенная над телом, всегда изменяет его кинетическую энергию:

. С другой стороны можно сказать, что если у тела меняется кинетическая энергия, то тело совершает работу.

10. Потенциальная энергия. Закон сохранения механической энергии. Потенциальная энергия связана с взаимным расположением тел в данной системе и, также как кинетическая энергия, может измеряться работой, которую может совершить система, переходя из одного состояния в другое. Найдем выражение потенциальной энергии для упруго сжатой (или растянутой) пружины. В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседни-ми витками пружины). Для того чтобы найти потенциальную энергию сжатой пружины, необходимо вычислить работу, затраченную на накопление этой энергии.

Потенциальная энергия растянутой пружины.

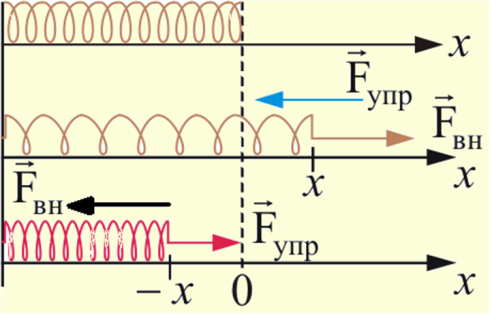
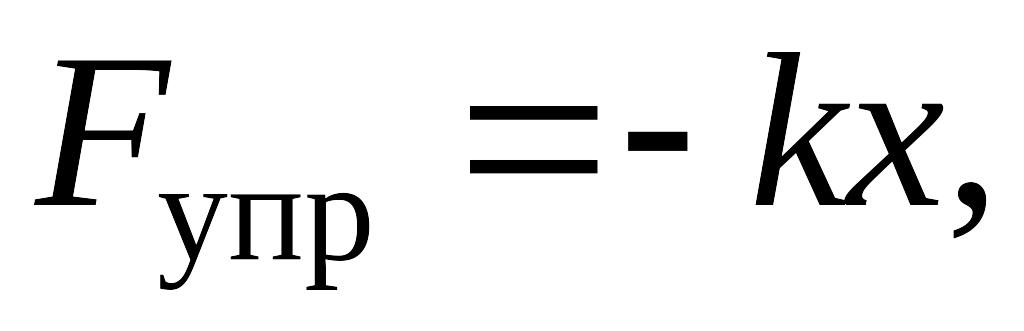Сила упругости

У пругие силы центральные, значит консервативные и имеет смысл говорить о U(r) деформированной пружины. Сила непостоянна, поэтому элементарная работа

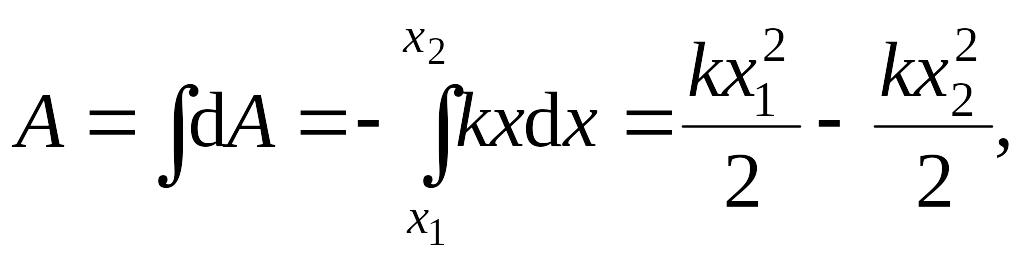
. Знак минус говорит о том, что работа совершена над пружиной. Т.е.

Потенциальной энергией обладают и тела, поднятые над поверхностью Земли.

Для поднятия тела массы m на высоту h необходимо совершить работу (при условии, что v = const) . Эта работа пойдет на увеличение энергии системы тело - Земля, т.е. . Считая, что в состоянии, когда тело находилось на поверхности Земли, потенциальная энергия системы U₁ = 0, получим A = U₂. Таким образом, потенциальная энергия тела, поднятого на высоту h над поверхностью Земли равна . Итак, работа, совершенная внутренними силами системы, и изменение потенциальной энергии связаны следующим образом:

Для вывода закона сохранения энергии рассмотрим простейший случай свободного падения тела. В данном случае система состоит из двух тел: падающего тела и земли. На тело будет действовать только сила тяжести F = mg. Под действием этой силы тело приобретает ускорение, т.е. его скорость падения по мере приближения к Земле будет увеличиваться, а это означает, что сила тяжести совершает работу, которая идет на изменение кинетической энергии тела

Т акже за счет силы тяжести происходит изменение взаимного расположения тела по отношени. к Земле, т.е. изменяется потенциальная энергия тела:

Т ак как работа совершена одной и той же силой, то можно записать следующее равенство или откуда

Величина W, равная сумме кинетической и потенциальной энергий, называется полной механической или просто энергией тела. Полученное соотношение выражает закон сохранения энергии тела. Этот закон формулируется следующим образом: в изолированной системе полная энергия неизменна. При переходе из одного состояния в другое кинетическая и потенциальная энергии переходят одна в другую, но их сумма остается неизменной. Под изолированной системой мы будем

понимать систему тел, в которой не действуют силы трения и сопротивления.