4 5. Закон полного внутреннего отражения.

Закон преломления можно представить в следующем виде: . Из этой формулы видно, что при переходе света из оптически более плотной среды в оптически менее плотную (n₁>n₂) луч света удаляется от нормали к поверхности

раздела двух сред, т.е. угол g больше угла a. Увеличение угла падения a сопровождается более быстрым ростом угла преломления g и, при достижении углом a значения a_пред = arcsin n_12. Угол g становится равным p/2. Угол падения, при котором угол преломления равен p/2, называется предельным углом падения.

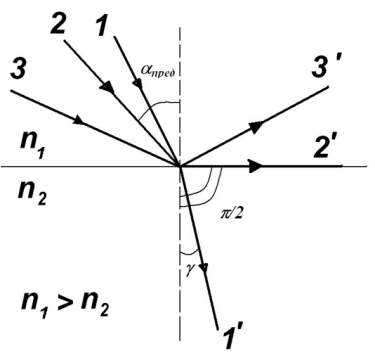
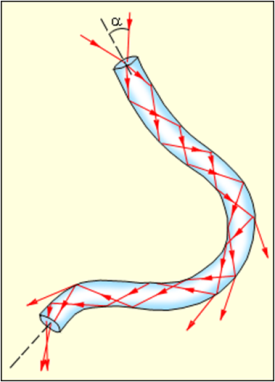
Если угол падения a будет больше предельного угла падения a_пред, то наблюдается явление полного внутреннего отражения: свет, падающей на границу раздела двух сред полностью отражается обратно в первую среду, а преломление прекращается. На измерении предельного угла падения основано устройство рефрактометров – приборов для определения показателя преломления жидкостей. Явление полного внутреннего отражения лежит в основе волоконной оптики. Свет, попадая внутрь прозрачного волокна, окруженного веществом с меньшим показателем преломления, многократно отражается и распространяется вдоль этого волокна. Диаметр этих тонких стеклянных или пластиковых волокон может быть доведен до нескольких микрометров. Для передачи больших световых потоков и сохранения гибкости светопроводящей системы отдельные волокна собираются в пучки (жгуты) – световоды, свет по световоду может передаваться почти без потерь.

Рис.3 демонстрирует, как распространяется свет по тонкому волокну, испытывая только скользящие отражения от стенок, т.е. полное внутреннее отражение.

46. Линзы. Собирающие линзы. Рассеивающие линзы.Формула тонкой линзы.

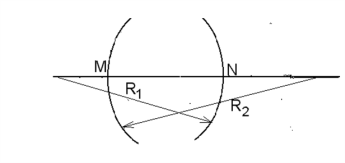
Прозрачное тело, ограниченное двумя сферическими поверхностями, называется линзой. Если расстоянием MN можно пренебречь по сравнению с R₁ и R₂, то линза называется тонкой. В этом случае точка М совпадает с точкой N, и тогда точка М будет называться оптическим центром линзы.

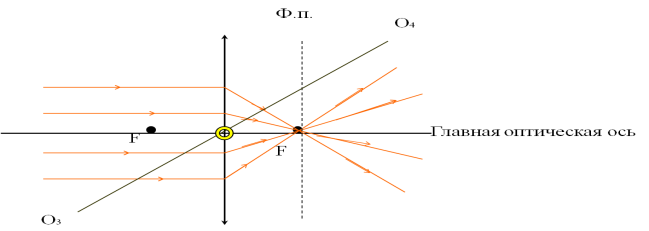
Главная оптическая ось – прямая, на которой лежат центры сферических поверхностей, ограничивающих линзу. Главный оптический центр линзы – точка, лежащая на главной оптической оси в центре линзы. Фокус – точка на главной оптической оси, в которой собираются лучи после преломления в линзе.

Фокальная плоскость линзы (Ф.п.)– плоскость, проходящая через главный фокус линзы перпендикулярно главной оптической оси. Побочная оптическая ось (О₃О₄) – прямая, проходящая через главный оптический центр линзы, всегда параллельная падающему лучу.

Линза называется положительной (собирающей), если ее фокусное расстояние положительно (F > 0). Собирающие линзы на рисунках представляют как:

Существуют три основных вида собирающих линз: 

     

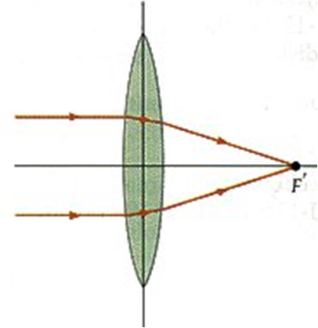
У собирающей линзы фокусы являются действительными, т.к. пересекаются сами лучи (рис. 8). Фокусное расстояние F расстояние от оптического центра до фокуса. Оптическая сила линзы D - величина, обратная фокусному расстоянию: D = 1 / F

Линза называется отрицательной (рассеивающей), если ее фокусное расстояние положительно (F < 0). Рассеивающие линзы на рисунках представляют как:

Есть три основных вида рассеивающих линз:

 

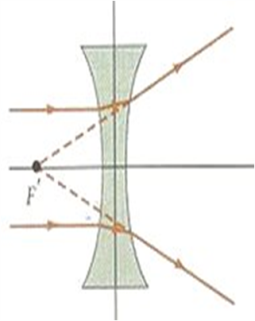
У рассеивающей линзы фокусы являются мнимыми, так как пересекаются продолжения лучей. Формула тонкой линзы для рассеивающей линзы выглядит следующим образом:

Формула тонкой линзы. Формула тонкой линзы связывает между собой рассто-

яния от предмета до линзы и от линзы до изображения с

ф окусным расстоянием линзы, для собирающей линзы

она записывается следующим образом: , где F - фокусное расстояние линзы; D - оптическая сила

л инзы; d - расстояние от предмета до центра линзы; f - расстояние от центра линзы до изображения. Линейное увеличение, даваемое линзой – это величина равная отношению линейных размеров изображения к линейным размерам самого предмета и находится как: , где H - высота изображения; h - высота предмета.

Построение изображения в тонкой линзе.

Чтобы построить изображение светящейся точки нужно из всего многообразия лучей, испускаемых ею, выбрать два, ход которых нам известен и найти их пересечение после преломления в линзе. В качестве таких лучей можно использовать любые из трех основных: 

1)Луч, падающий на линзу параллельно какой-либо оптической оси, после преломления пройдет через фокус, лежащий на этой оптической оси;

2) Луч, идущий через оптический центр линзы, не меняет своего направления;

3) Луч, проходящий через передний фокус, после преломления в линзе пойдет параллельно главной оптической оси

Правила хода лучей в рассеивающей линзе

1)Лучи, падающие на линзу параллельно какой-нибудь оптической оси, после преломления пойдут так, что их продолжения пройдут через фокус, лежащий на оптической оси;

2) Луч, идущий через оптический центр линзы, не меняет своего направления.

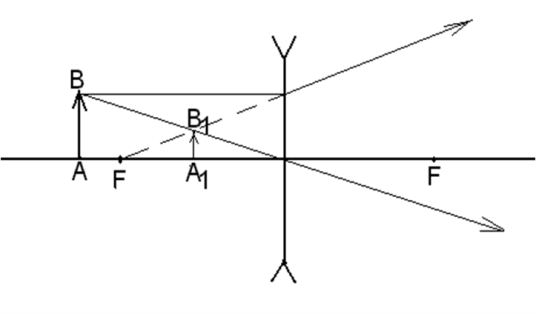
На рисунке 11 показано построение изображения А₁В₁ предмета АВ в рассеивающей линзе

.