Некоторые методы решения типовых задач Поиск экстремальных значений (максимума, минимума) в одномерном массиве
Рассмотрены только специфические особенности задачи.
1. Задача Extr. Найти номер и значение максимального элемента в одномерном массиве a[n].
Пример, на базе которого затем построим тесты.
Возьмем n=6 и изображенные ниже значения элементов.
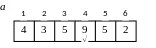
Максимальный элемент равен 9, его номер равен 4.
2. Входные данные
цел n - число элементов массива; простая переменная; ...
вещ а - заданный одномерный массив; .....
3. Выходные данные
цел kmax - номер максимального элемента; ....
вещ amax - его значение; ....
4. Аномалии не рассматриваем
5. Функциональные тесты составить самостоятельно. Рассмотреть следующие варианты входных данных:
1) один экстремум в середине массива;
2) более одного экстремума (несколько равных максимумов/минимумов);
3) все равные элементы.
6. Метод
Рассмотрим процесс поиска максимума и его номера на примере, приведенном после условия задачи.
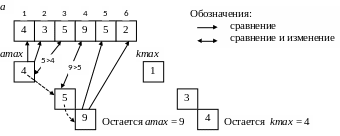
Просматривая поочередно все элементы массива, сравниваем каждый из них с текущим значением максимума (amax).
Если текущий элемент больше amax, то заменяем значение amax на значение текущего элемента, а значение kmax - на его номер.
Сначала возьмем amax=a[1], kmax=1.
Пусть i - текущий индекс элемента. Описание метода приобретает вид:
amax:=a[1]; kmax:=1;
повторяем для всех элементов массива (для i от 1 до n):
если a[i]>amax то
amax:=a[i];
kmax:=i;
конец если;
конец повторения;
● Для поиска минимума знак ">" следует заменить на "<".
● В целочисленном массиве элементы могут совпадать. При поиске номера требуется уточнение: найти номер первого или последнего максимума (минимума).
Например, в массиве a = (1,9,2,3,9,7) amax=9; kmax=2 при поиске первого максимума и kmax=5 при поиске последнего максимума.
При поиска первого максимума (минимума) в условии приведенного алгоритма должен стоять знак строгого неравенства > (<); при поиске последнего – неравенство заменяется на нестрогое: >= (<=).
● Экстраполируем приведенный алгоритм для поиска экстремума cmax в матрице c[m,n] и его индексов imax, jmax
Просмотр начинаем с первого элемента (i=1, j=1)! Иначе потеряется целый столбец или строка.
При обработке матрицы по столбцам действия аналогичны.
● Варианты поиска максимального элемента и его номера в одномерном массиве
Массив можно просматривать с начала либо с конца. Порядок просмотра задается начальным и конечным значением индекса и шагом его изменения.
В качестве начального значения максимума можно выбрать первый либо последний элемент.
При просмотре массива текущее значение максимума может изменяться либо если текущий элемент оказался строго больше, либо если он оказался не меньше.
Получим следующие схемы поиска.
•• Поиск номера первого максимального элемента
-
С начала
С конца
amax:=a[1]; kmax:=1;
для i от 1 до n шаг +1 цикл
если a[i] > amax то
amax:=a[i]; kmax:=i;
кесли;
кц;
amax:=a[n]; kmax:=n;
для i от n до 1 шаг -1 цикл
если a[i] >= amax то
amax:=a[i]; kmax:=i;
кесли;
кц;
•• Поиск номера последнего максимального элемента
-
С начала
С конца
amax:=a[1]; kmax:=1;
для i от 1 до n шаг +1 цикл
если a[i] >= amax то
amax:=a[i]; kmax:=i;
кесли;
кц;
amax:=a[n]; kmax:=n;
для i от n до 1 шаг -1 цикл
если a[i] > amax то
amax:=a[i]; kmax:=i;
кесли;
кц;