
- •1.Классификация событий. Классическое определение вероятности.
- •2. Элементы комбинаторики: перестановки, сочетания, размещения, правило умножения и сложения.
- •4. Частота события. Стат. Определение вероятности.
- •5. Условная вероятность. Теорема умножения вероятностей. Независимость событий.
- •6. Формула полной вероятности. Формулы Байеса.
- •7. Повторные независимые испытания. Ф-ла Бернулли.
- •3. Действия над событиями. Соотношения между событиями. З-н сложения вероятностей.
- •9. Понятие случайной величины и ее ф-ии распр-ния.
- •8. Формула Пуассона. Локальная и интегральная предельные теоремы Лапласа.
- •11. Биномиальное распределение.
- •12. Распределение Пуассона.
- •10.Дискретные случайные величины. Числовые характеристики случайных величин.
- •22. Точечные и интервальные оценки. Доверительная вероятность и доверительный интеграл.
- •23. Доверительный интервал для оценки мат. Ожидания нормального распределения.
- •19. Оценка параметров по выборке. Понятие несмещенности, состоятельности и эффективности оценки.
- •21.Связь между хар-ми генеральной и выборочной совокупностей. Точечное оценивание.
- •17. Теоремы Чебышева и Бернулли. Центральная предельная теорема.
- •46. Градиентные методы. Методы наиск-его подъёма.
- •33. Различные формы записи задач линейного программирования.
- •41. Способы построения исходного опорного плана транспортной задачи.
- •13.Непрерывные случайные величины. Плотность распределения. Числовые хар-ки
- •16. Нормальное распределение. Вероятность попадания в заданный интервал нормальной св. Правило трех сигм.
- •14. Равномерное распределение. Показательное распределение. Вероятность попадания св в заданный интервал.
- •16. Понятие о з-не больших чисел. Неравенства Маркова и Чебышева.
- •45. Выпуклые и вогнутые функции и их свойства.
- •44. Градиент функции и его свойства.
- •18. Выборочный метод. Основные понятия. Полигон и гистограмма. Эмпирическая ф-ия распределения.
- •40.Постановка транспортной задачи по критерию стоимости в матричной форме.
- •47.Общая постановка задачи динамического программирования. Принцип оптимальности р.Беллмана.
- •50.Парные матричные игры с нулевой суммой.
21.Связь между хар-ми генеральной и выборочной совокупностей. Точечное оценивание.
Оценка назыв. точечной если она выражается одним числом. К ней относятся хар-ки выборочной сов-ти являющиеся точечными оценками соотв. хар-к генеральной сов-ти. Выборочную среднюю и выборочную дисперсию принимают в кач-ве оценки генеральной средней и генеральной дисперсии соотв.
Можно док-ть, что:
М(
 )=
)= )
)Р( )=
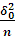 =
=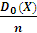 (1.11)
(1.11)M(δ2)=

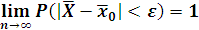
Из
1.11. следует что средняя выборки
явл. несмещенной
и состоятельной оценкой
средней генер.
,
т.к. в 1.11
выполняется рав-во 1 при n→∞
выборочная средняя стремится по
вероятности к генер. средней (рав-во 4).
Оценка
явл. также эффективной.
Выборочная дисперсия явл. смещенной
оценкой генер. дисперсии. Чтобы получить
несмещенную оценку генер. дисперсии
вводят понятие так называемой эмпирической
(исправленной) дисперсии (S2=![]() δ2
) – явл.
несмещенной оценкой
генер. дисперсии; состоятельной.
Для оценки
сред. квадрат. отклонения генер. сов-ти
служит «испарвленное» ср. квадрат.
отклонение или эмпирический стандарт.
S=
δ2
) – явл.
несмещенной оценкой
генер. дисперсии; состоятельной.
Для оценки
сред. квадрат. отклонения генер. сов-ти
служит «испарвленное» ср. квадрат.
отклонение или эмпирический стандарт.
S=![]() .
Замечание: оценкой
дисперсии пользуются обычно при малых
выборках, т.е. практически при n<30,
т.к. при больших n,
вычисл. по формулам δ2
и S2
незнач. Отличаются друг от друга.
.
Замечание: оценкой
дисперсии пользуются обычно при малых
выборках, т.е. практически при n<30,
т.к. при больших n,
вычисл. по формулам δ2
и S2
незнач. Отличаются друг от друга.
17. Теоремы Чебышева и Бернулли. Центральная предельная теорема.
Теорема
4: если СВ
х1,
х2,
…, хn
независимы, имеют мат. ожидания и
дисперсии, каждая из которых ограничена
одним и тем же числом С, то для любого
ε>0 выполняется нерав-во: P(|![]() (4.5.). Следовательно:
(4.5.). Следовательно:
![]() (4.6.)
(4.6.)
Последовательность
числе А1,
А2,
…, Аn
назыв. равномерно
ограниченной,
если сущ. такая постоянная С, что для
любого i
выполняется нерав-во |Аi|≤C,
где i=1,2,…,
n
(т.е. каждое из чисел ограничено одним
и тем же числом). З-н
больших чисел Чебышева: при
неограниченном увеличении числа n
попарно независимых СВ, имеющих М(Х) и
равномерно ограниченной дисперсии, их
среднее арифмет. стремится по вероятности
к средней арифмет. их мат. ожиданий. Ф-ла
4.6. означает, что с увеличением числа n
нерав-во в скобках будет выполняться в
подавляющем числе случаев, нерав-во же
противоположного смысла практически
невозможно. Следствие:
если Х1,
Х2,
…, Хn
– последовательность независимых СВ,
мат. ожидания каждой из которых равны
а, а дисперсия – δ2,
то нерав-во 4.5. и ф-ла 4.6 принимают вид:
P(|![]()
![]()
Теорема 4: если m-число появлений события А в n независимых испытаниях, р-вероятность появления события в каждом испытании, то вероятность того, что отклонение относительной частоты m/n от вероятности |р| меньше числа ε>0, выражается неравенством:
P(|![]()
![]()
З-н больших чисел в ф-ле Бернулли: при неограниченном увеличении числа n повторных независимых испытаний относительная частота появления события стремится по вероятности к вероятности события при данном испытании. Теорема 5 (теорема Ляпунова, один из вариантов центральной предельной теоремы): если х1, х2, …, хn – независимые СВ, имеющие одно и то же распределение с мат. ожиданием а и дисперсией δ2, то при неограниченном возрастании n з-н распределения суммы х=х1+х2+…хn неограниченно приближается к нормальному. Следствие: если СВ х1, х2, …, хn удовлетворяют условию теоремы, то их среднее арифмет. при достаточно большом n также имеет распределение близкое к нормальному. Ляпунов показал также, что требование одинакового распределения хi можно заменить условием их равномерной малости в образовании общей суммы. Поэтому центрально предельную теорему можно сформулировать и т.о.: если СВ Х предст. собой сумму очень большого числа взаимно независимых СВ, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному. Практ. исп-ие центральной теоремы: ошибки измерения, выборочное наблюдение, рассеивание при стрельбе. К предельным теоремам относятся также локальная и интегральная теоремы Лапласса.
