Итак, нам нужно найти площадь области d . Как известно .

Перейдем к двукратному интегралу, пусть внешней – будет переменная x, а внутренней – y. Для определения внешней переменной x, решим уравнение . Отсюда получаем, что внешняя переменная x меняется от (-2) до 1. Для определения пределов внутреннего интеграла по переменной y, движемся снизу вверх параллельно оси (OY) на входе в область пересекаем параболу - нижний предел внутреннего интеграла. На выходе из области интегрирования пересечем прямую - верхний предел внутренней переменной. Т аким образом искомая площадь:

3. Вычислить объем тела, ограниченного поверхностями: ; ; ; ; .

Решение.

Итак, тело, объем кторого нужно вычислить, ограничено координатными плоскостями ( ; ; ), плоскостью , параллельной оси (OZ) и параболоидом .

1способ.

Как известно . Перейдем к двукратному интегралу, причем y – внешняя переменная, а x – внутренняя переменная. , уравнение поверхности, которая ограничивает тело V сверху. Итак: ; внешняя переменная y меняется от 0 до 1(см. область D). Для определения пределов внутренней переменной x движемся слева направо параллельно оси (OX), на входе в область D пересекаем прямую - нижний предел переменной y; на выходе из области D пересекаем прямую - верхний предел переменной y.

Таким образом,

продолжение№1

4.Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями и

В случае однородной пластины занимающей область D плоскости (XOY), координаты центра тяжести x_c, y_c находят по формулам

;

В рассмотренном случае фигура ограничена кривыми и при x изменяющемся от 0 до 3.

Поэтому продолжение №2(обратить внимание)

Индивидуальное задание № 6

по теме « Интегралы.»

Вариант 1

1. Исследовать сходимость интеграла

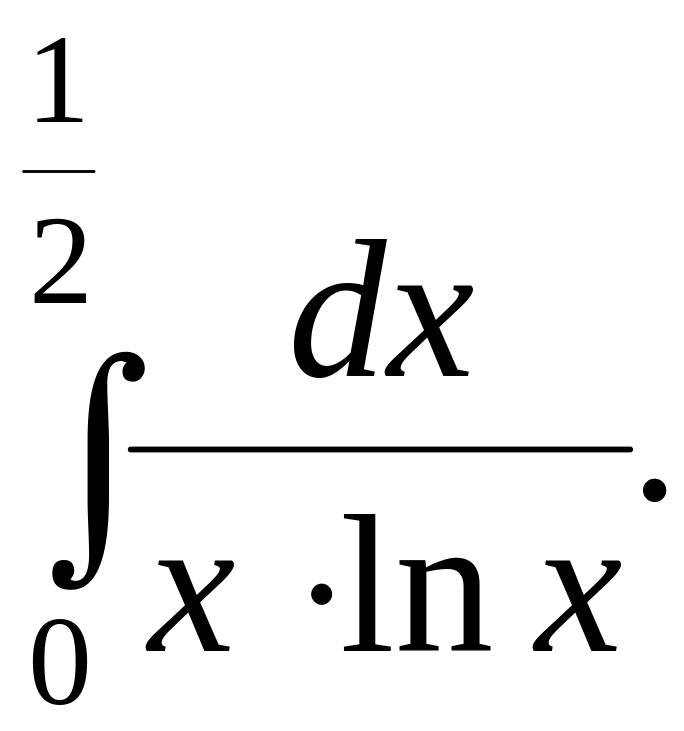
2. Вычислить площадь фигуры, ограниченной линиями

3. Вычислить объем тела вращения вокруг оси фигуры, ограниченной астроидой

4. Вычислить координаты центра тяжести фигуры, ограниченной линиями

Вариант 2

1. Вычислить площадь фигуры, ограниченной линиями :

а) с помощью определенного интеграла;

б) с помощью двойного интеграла;

в) с помощью криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями Сделать рисунок.

3. Вычислить координаты центра тяжести фигуры, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 3

1. Вычислить площадь фигуры, ограниченной линиями , с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

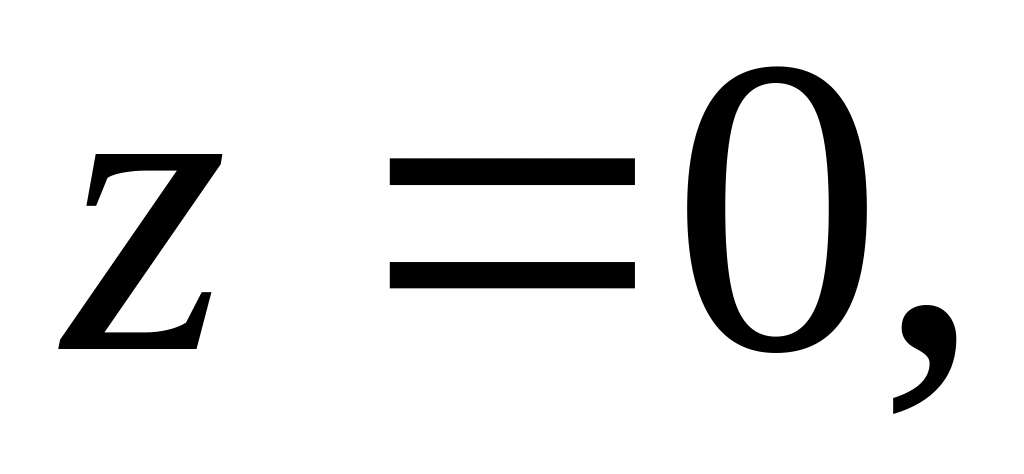
2. Вычислить объем тела, ограниченного поверхностями Тело изобразить на рисунке.

3. Найти координаты центра тяжести плоской однородной области, ограниченной линиями

4. исследовать сходимость интеграла

Вариант 4

1. Вычислить площадь плоской области, ограниченной линиями , с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести фигуры, ограниченной линиями

4. Исследовать сходимость интеграла

К задачам 1-3 сделать рисунки.

Вариант 5

1. Вычислить площадь плоской области, ограниченной линиями . с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести фигуры, ограниченной линиями

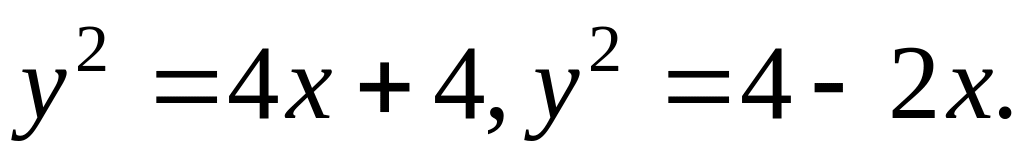
4. Исследовать сходимость интеграла

К задачам 1-3 сделать рисунки.

Вариант 6

1. Вычислить площадь плоской области, ограниченной линиями , с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести фигуры, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 7

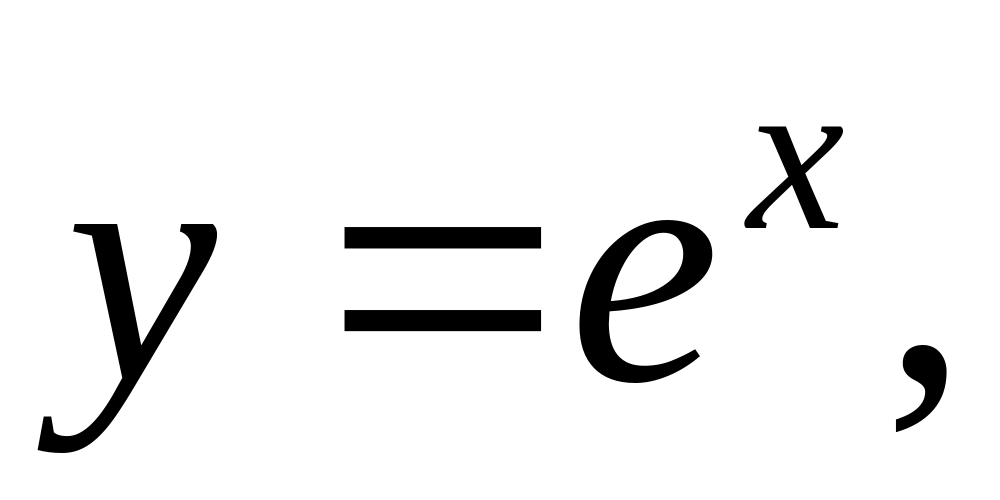
1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

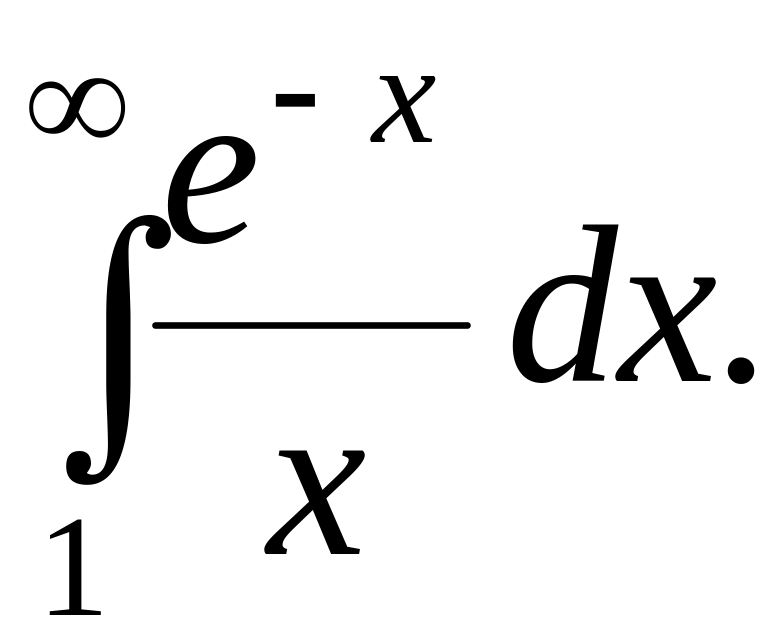
Вариант 8

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

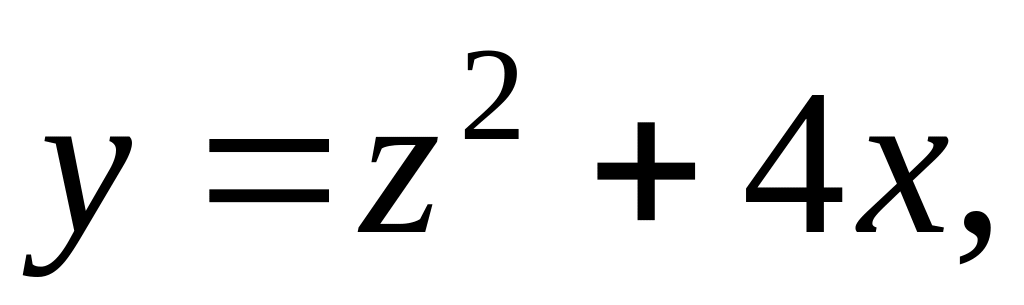
3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 9

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 10

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной полусферы

4. Исследовать сходимость интеграла

Вариант 11

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить длину дуги линии от до

4. Исследовать сходимость интеграла

Вариант 12

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить длину дуги астроиды

4. Исследовать сходимость интеграла

Вариант 13

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить длину одной арки циклоиды

4. Исследовать сходимость интеграла

Вариант 14

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 15

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить длину дуги линии от до

4. Исследовать сходимость интеграла

Вариант 16

1. Вычислить площадь плоской области, ограниченной линиями 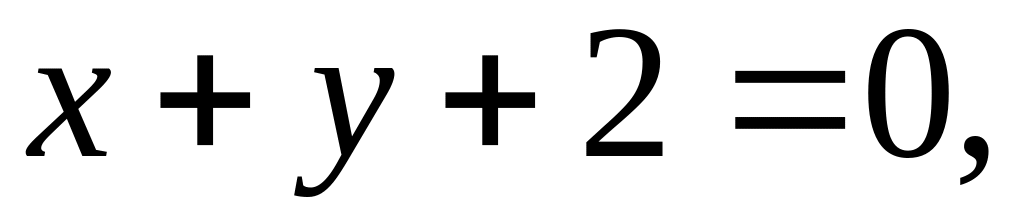с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 17

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 18

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной кардиоидой

4. Исследовать сходимость интеграла

Вариант 19

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 20

1. Вычислить площадь плоской области, ограниченной линиями , с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

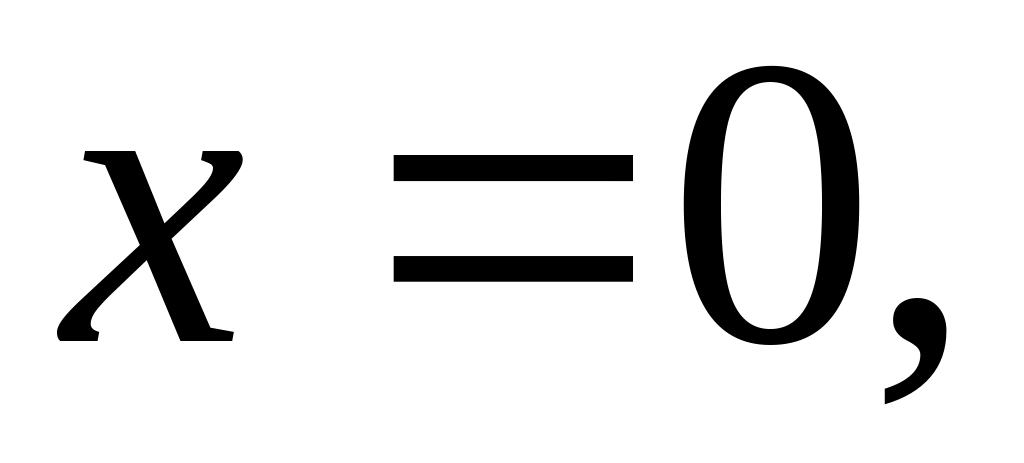
3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла .

Вариант 21

1. Вычислить площадь плоской области, ограниченной линиями , с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной первой аркой циклоиды

4. Исследовать сходимость интеграла

Вариант 22

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела вращения вокруг оси фигуры, ограниченной линиями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 23

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

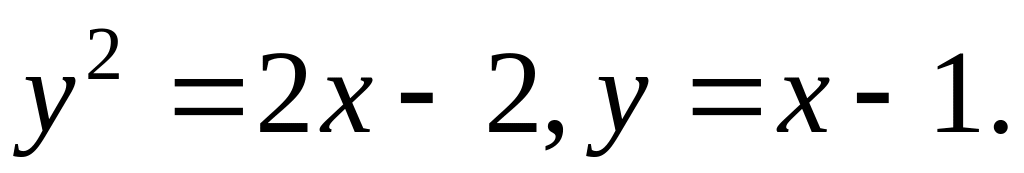
4. Исследовать сходимость интеграла

Вариант 24

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной одной аркой циклоиды

4. Исследовать сходимость интеграла

Вариант 25

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями x=4,

3. Вычислить длину кардиоиды

4. Исследовать сходимость интеграла

Вариант 26

1. Вычислить площадь плоской области, ограниченной линиями 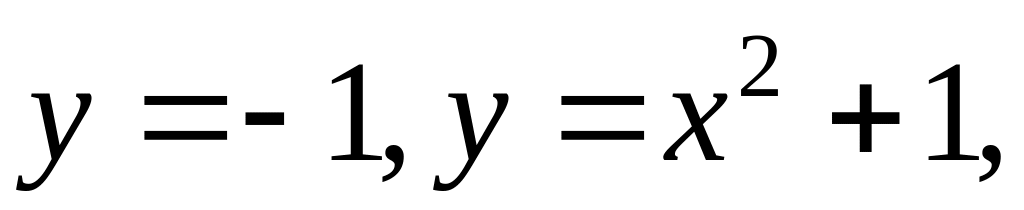с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить длину дуги кривой от до

4. Исследовать сходимость интеграла

Вариант 27

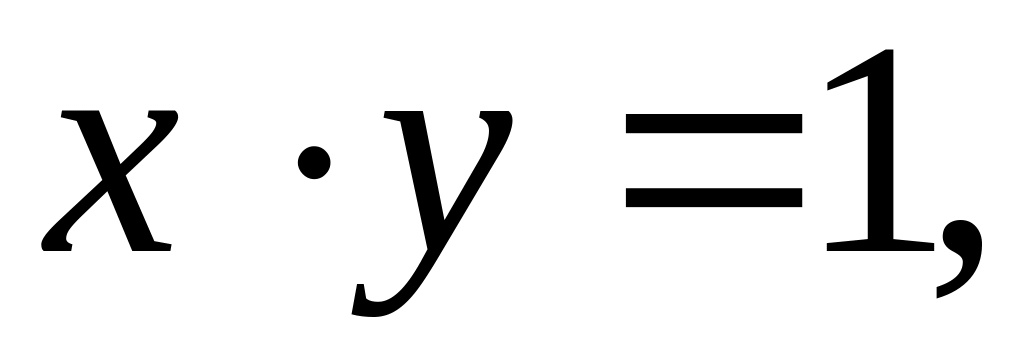
1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 28

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла

Вариант 29

1. Вычислить площадь плоской области, ограниченной линиями с помощью

а) определенного интеграла;

б) двойного интеграла;

в) криволинейного интеграла.

2. Вычислить объем тела, ограниченного поверхностями

3. Вычислить координаты центра тяжести однородной области, ограниченной линиями

4. Исследовать сходимость интеграла