
- •Кафедра высшей математики сборник контрольных работ и индивидуальных заданий по высшей математике
- •Индивидуальное задание № 1 по теме «Аналитическая геометрия на плоскости.»
- •Пример 2. В полярной системе координат построить график функции (без исследования). Записать уравнение, построенной кривой в декартовых координатах.
- •Индивидуальное задание № 4 по теме: Определенный интеграл.
- •Индивидуальное задание № 5 по теме “ Кратные интегралы и их приложения ”
- •Задание №2: Вычислить площадь фигуры, ограниченной линиями
- •Задание №4: Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями.
- •Итак, нам нужно найти площадь области d . Как известно .
- •Индивидуальное задание №7
- •Контрольная работа №2 по теме “ Вычисление пределов”.
- •Контрольная работа №3
- •Вариант 1
- •Вариант 1
Индивидуальное задание № 5 по теме “ Кратные интегралы и их приложения ”
Задание № 1: Построить на плоскости XOY область интегрирования. Изменить порядок интегрирования и вычислить двукратный интеграл при заданном и измененном порядках интегрирования.
 16)
16)
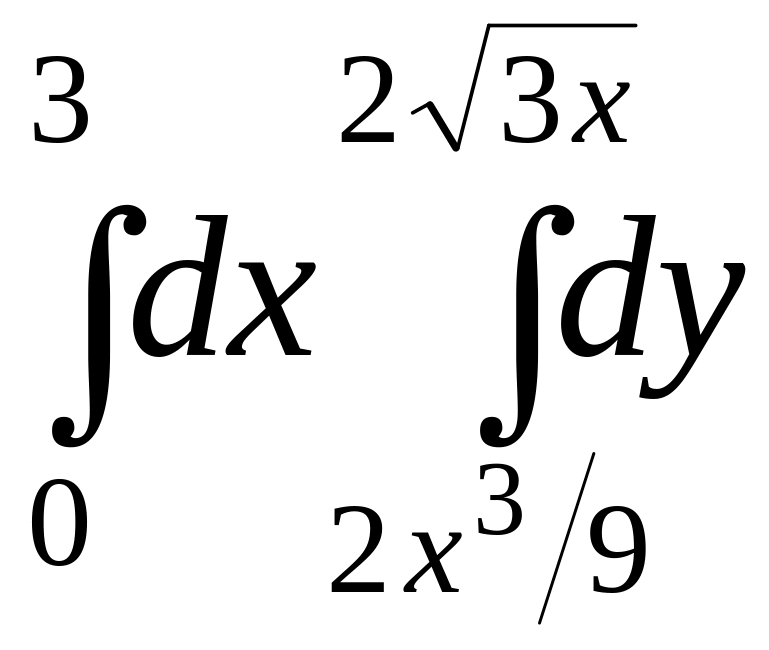
 17)
17)

 18)
18)

 19)
19)

 20)
20)

 21)
21)

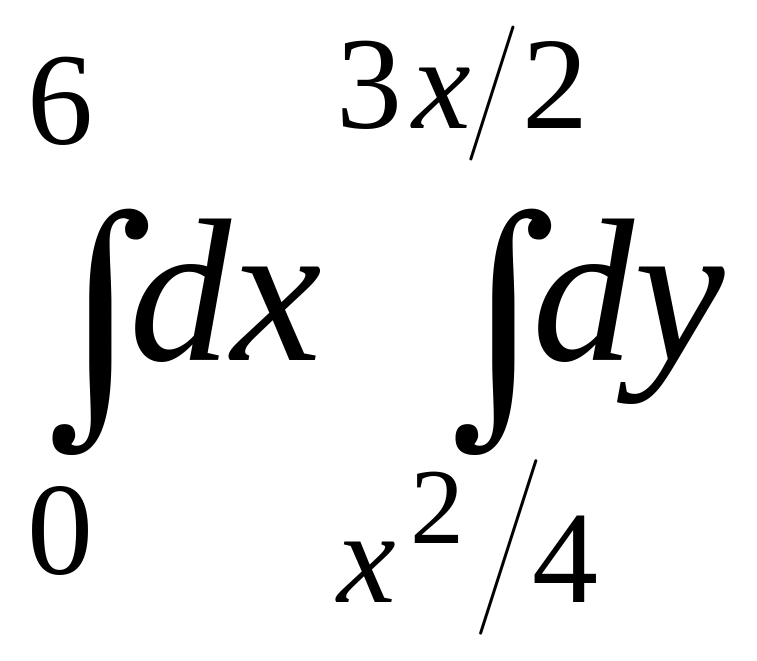 22)
22)
 23)
23)

 24)
24)

 25)
25)

 26)
26)

 27)
27)

 28)
28)

 29)
29)

 30)
30)
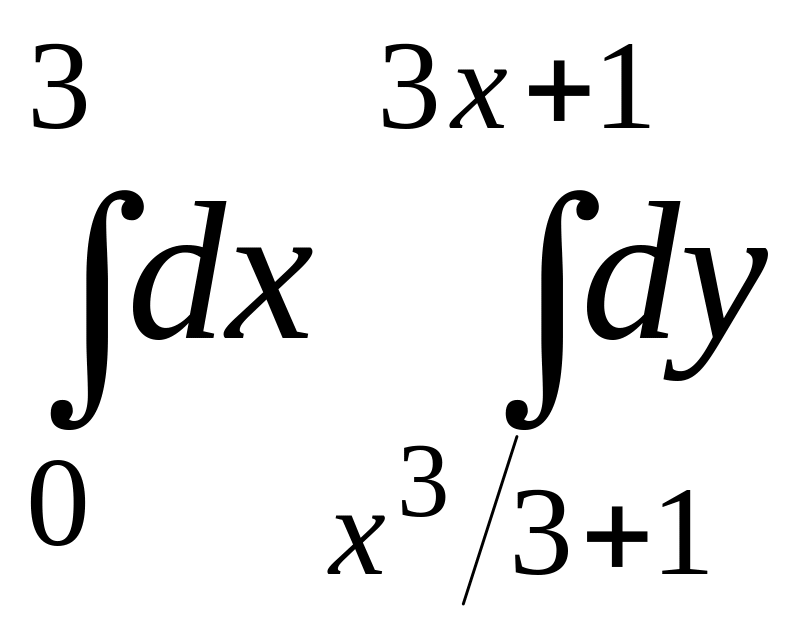
Задание №2: Вычислить площадь фигуры, ограниченной линиями
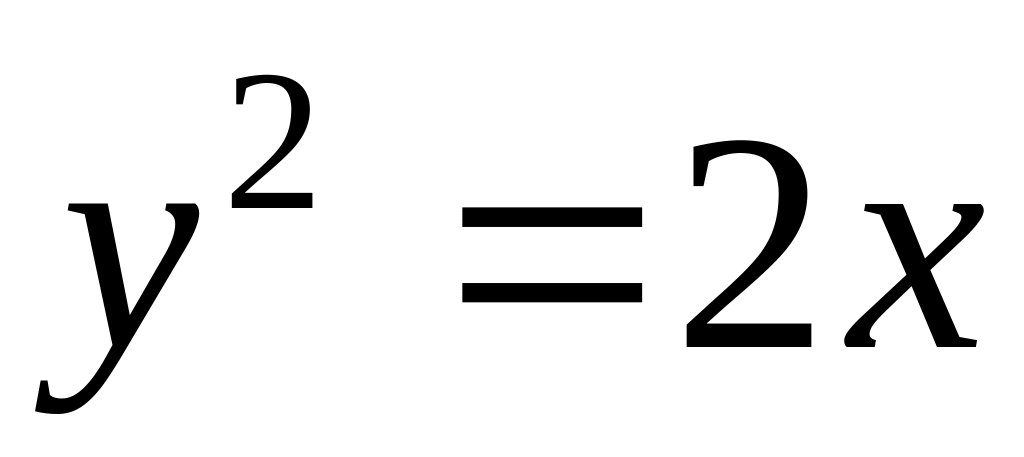 ;
;

 ;
;
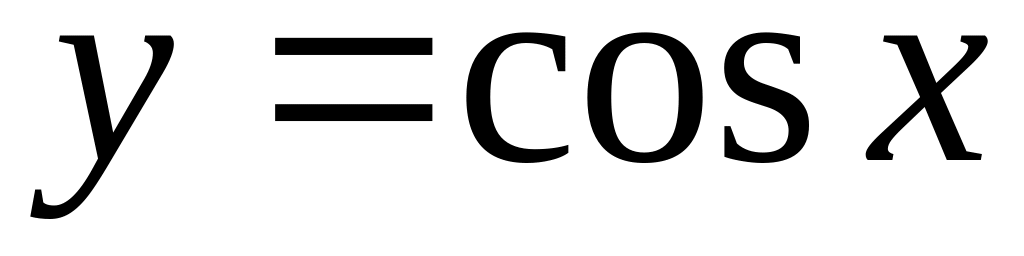 ;
;
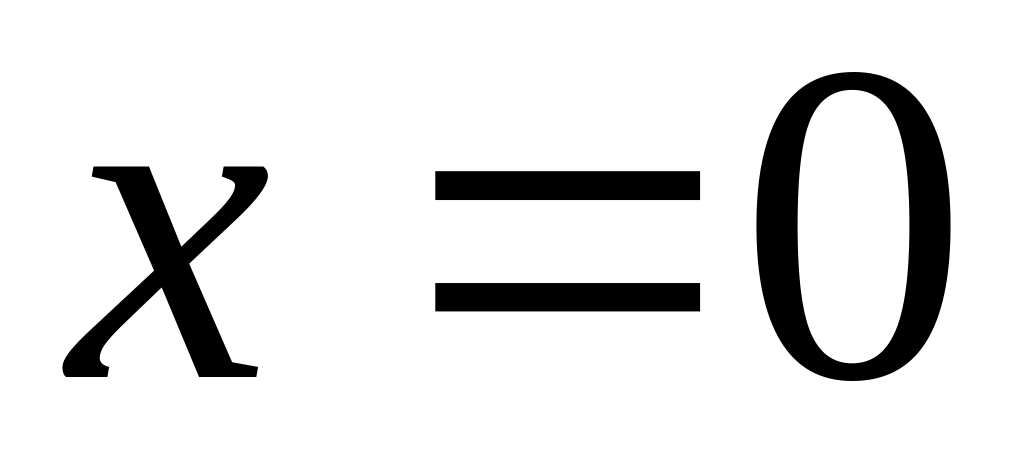
 ;
;

петлей кривой

 ;
;

 ;
;
 ;
;


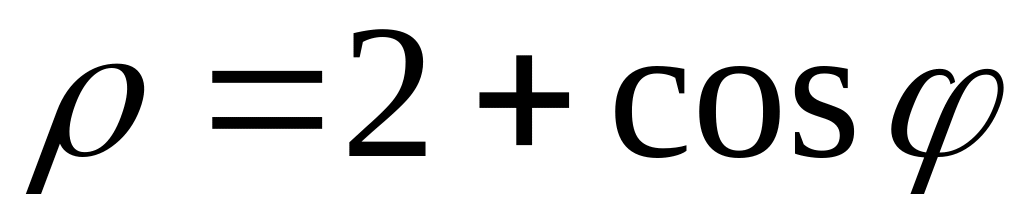
 ;
;

 ;
;

 ;
;

 ;
;

;
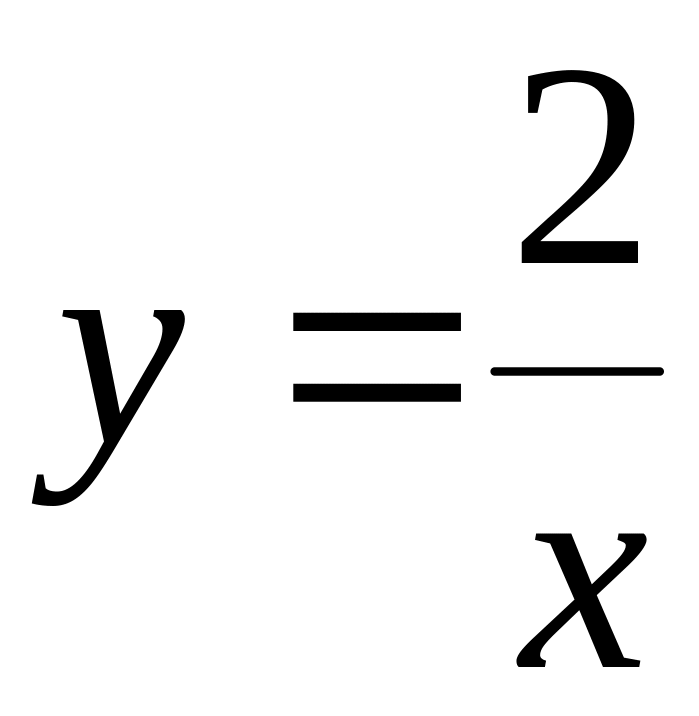 ;
;

 ;
;

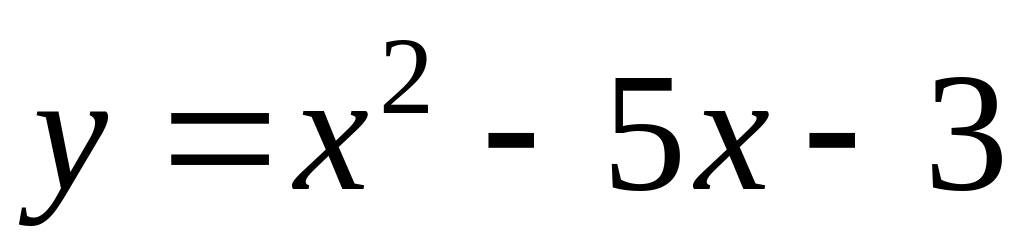 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;
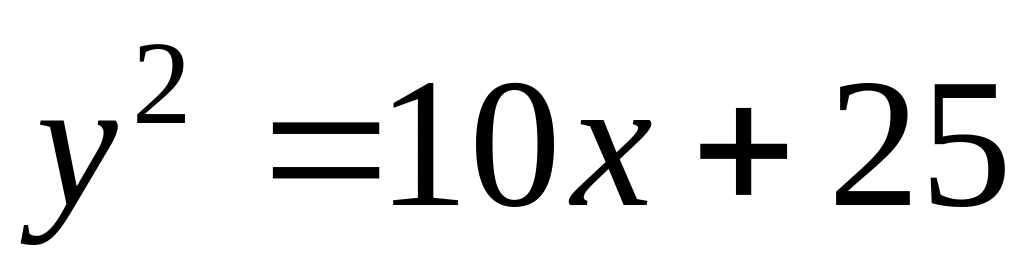 ;
;
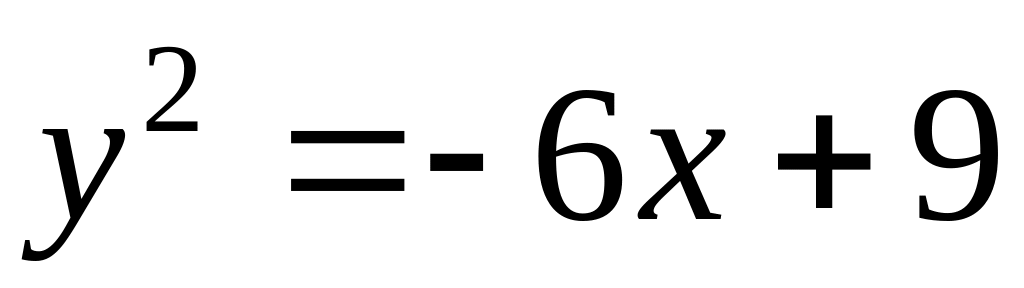
;
 ;
;

 ;
;

 ;
;
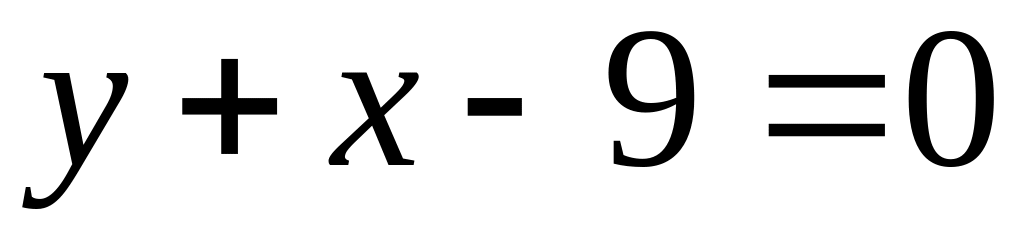
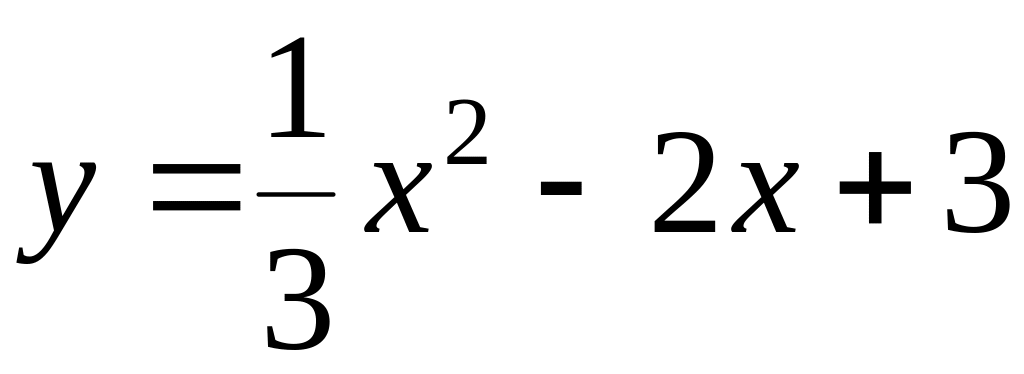 ;
;

; ;
;

Задание №3: Вычислить объём тела, ограниченного поверхностями (построить тело)
 ;
;
 ;
;
;
; ;
;
 ;
;
 ;
; ;
;
 ;
;
;
; ;
;
;
;
 ;
;
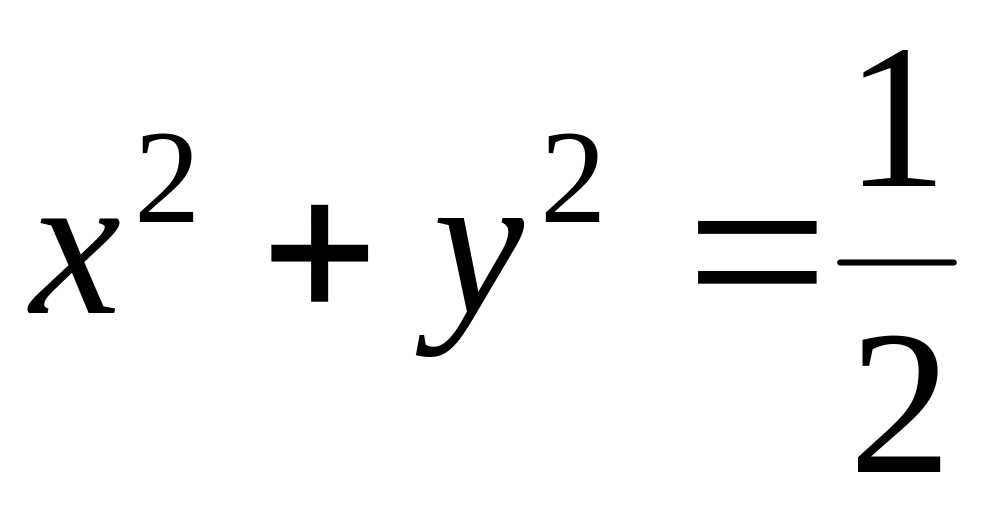 ;
;
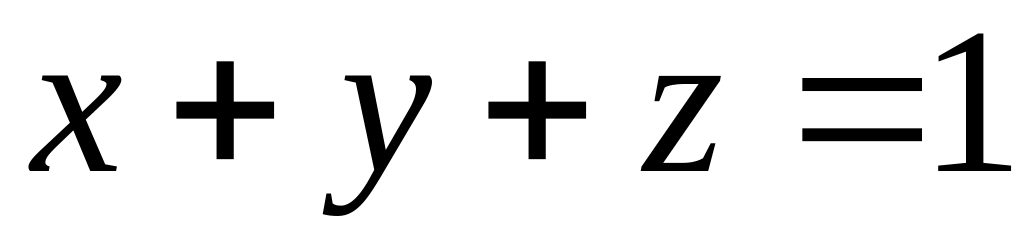 ;
;
 ;
;
;
; ;
;
 ;
;
;
;
;
;
;
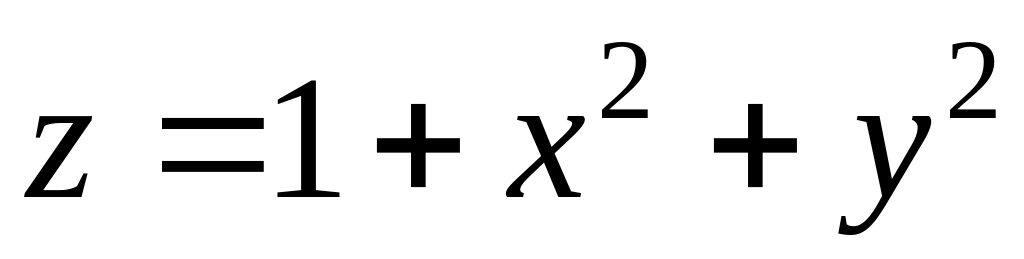
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;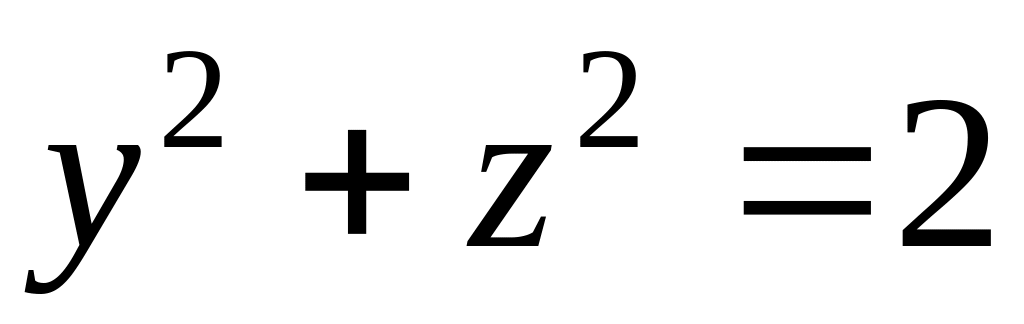
 ;
; ;
;
 ;
;
; ; ;
 ;
; ;
;
;
;
;
;
 ;
;
;
;
;
;
;
; ; ;
 ;
;
 ;
;
 ;
;
;
;
;
 ;
;
;
;
;
;
 ;
;
;
;
;
;
 ;
;
;
;
;
;
;
;
; ; ; ;

 ;
;
;
;
;
;
;
;
 ;
; ;
;
;
;
 ;
;
;
;
;
;
;
;
 ;
;
;
;
;
;
;
;
 ;
;
;
;
;
;
;
;
Задание №4: Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями.
 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

;

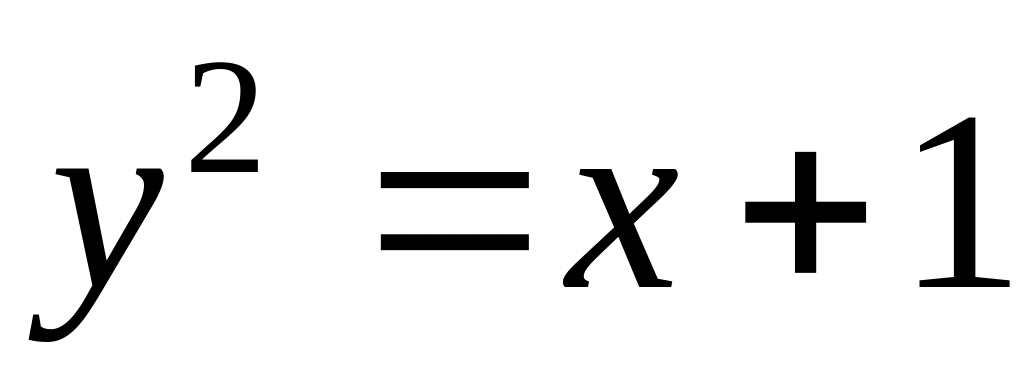 ;
;
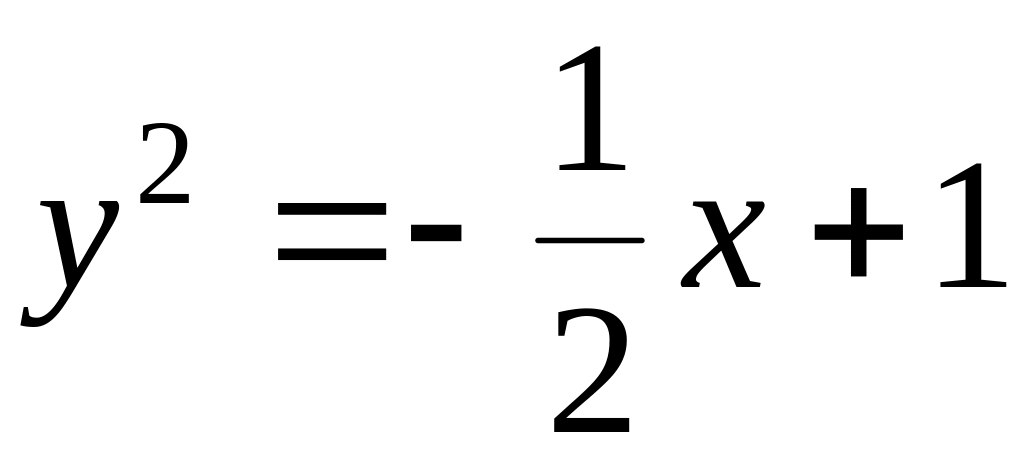
 ;
;

 ;
;
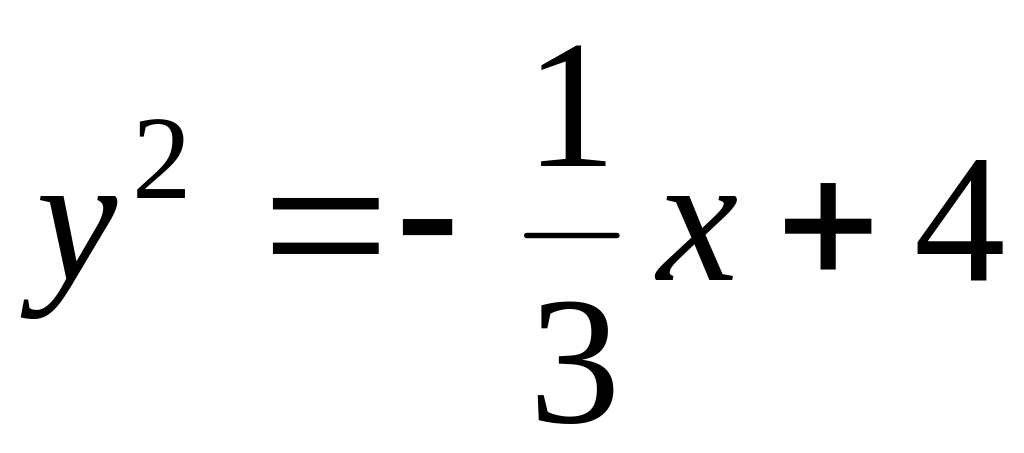
 ;
;

 ;
;

 ;
;

 ;
;
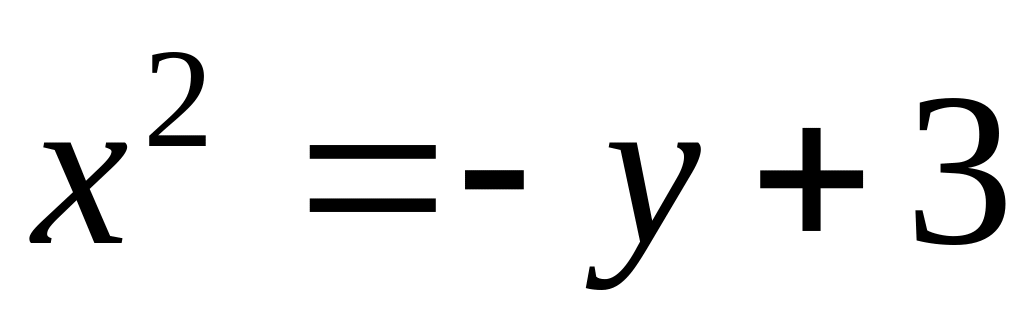
 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

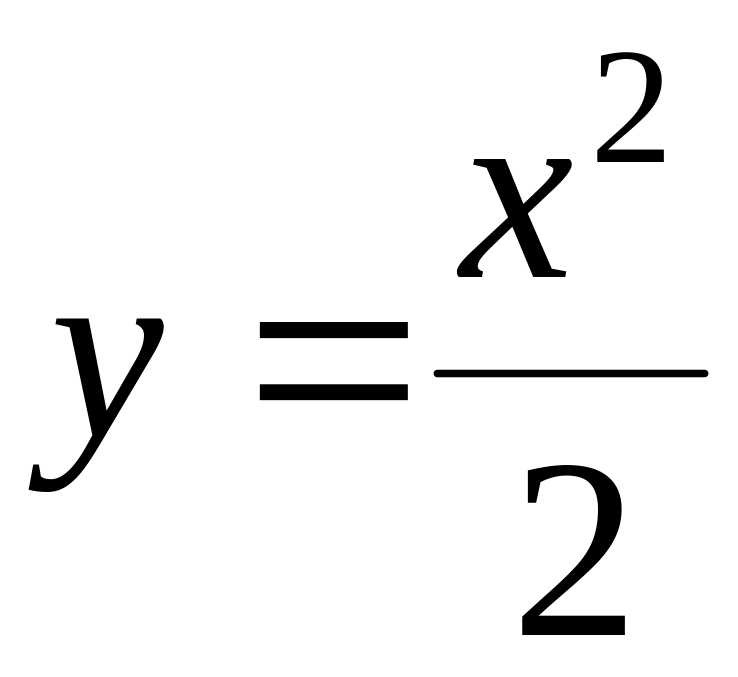 ;
;

 ;
;

(в первой четверти)
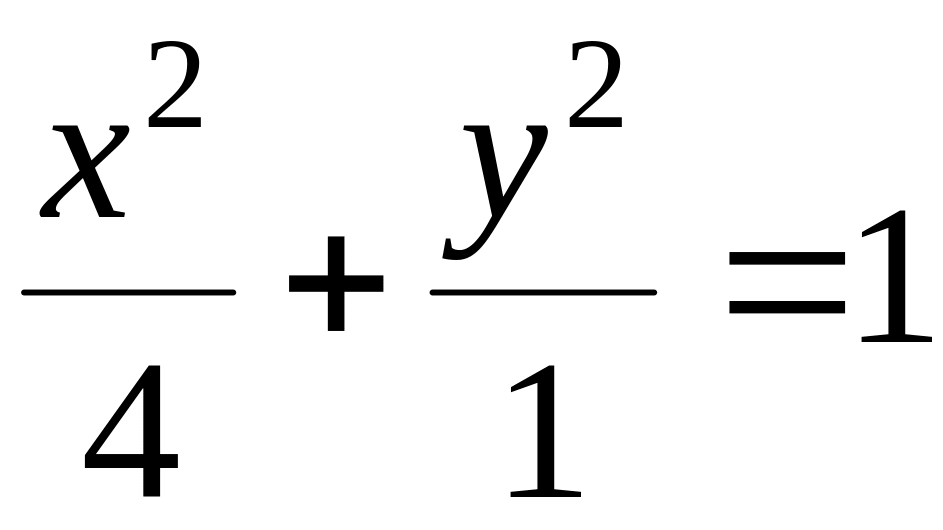 ;
(в
первой четверти)
;
(в
первой четверти) ;
;
;
;
Задание №5. Вычислить двойной интеграл, переходя к полярным координатам.
 ,
где D
ограничена
осью OX
и верхней
полуокружностью
,
где D
ограничена
осью OX
и верхней
полуокружностью

 ,
где D
ограничена окружностью
,
где D
ограничена окружностью

 ,
где D
ограничена окружностью
,
где D
ограничена окружностью
 и
окружностью
и
окружностью
 и
и

 ,
где D
ограничена окружностью
,
где D
ограничена окружностью
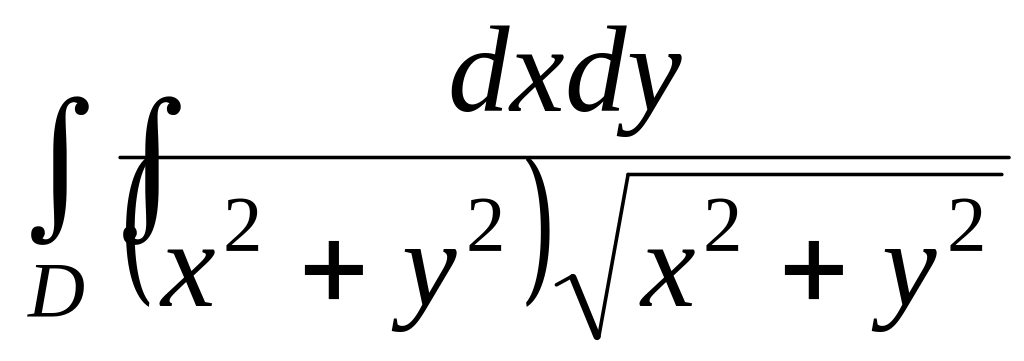 ,
где D
ограничена осями координат и прямыми
,
,
где D
ограничена осями координат и прямыми
,
 ,
где D
ограничена лемнискатой
,
где D
ограничена лемнискатой

 ,
где D
ограничена линиями
,
где D
ограничена линиями
 ;
;

, где D ограничена окружностью

, где D - первая четверть круга

, где D ограничена кардиоидой

, где D ограничена линией
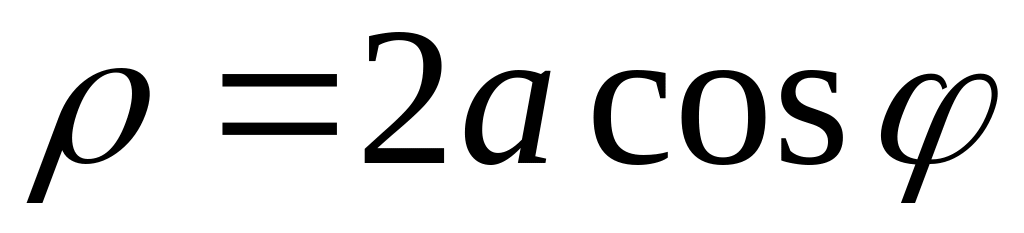
, где D ограничена кардиоидой

, где D ограничена петлей кривой

, где D ограничена линией
 ,
где D
ограничена линией
,
где D
ограничена линией







, где D ограничена прямыми , и дугой окружности , лежащей в первой четверти
 ,
где D-
круг с центром в начале координат и с
радиусом, равным 1
,
где D-
круг с центром в начале координат и с
радиусом, равным 1 ,
где D
есть
верхний полукруг с центром в точке
(3;0) и с радиусом равным 3 при чем
,
где D
есть
верхний полукруг с центром в точке
(3;0) и с радиусом равным 3 при чем

 ,
где D
ограничена линией
,
где D
ограничена линией
 (a>0)
(a>0), где D ограничена линиями и

 ,
где D-
круг с центром в начале координат и с
радиусом, равным 2
,
где D-
круг с центром в начале координат и с
радиусом, равным 2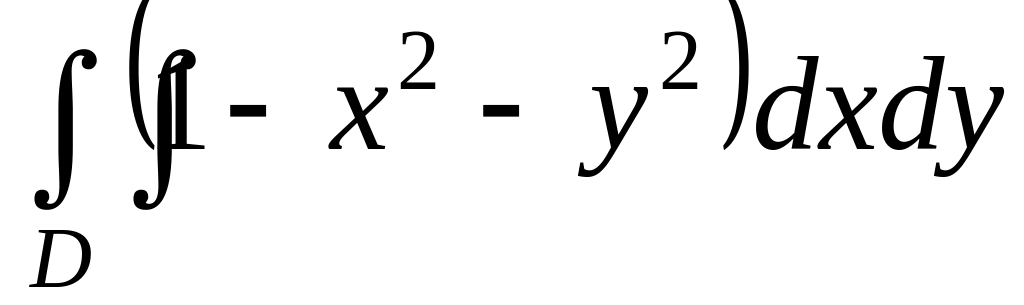 ,
где D
есть круг
,
где D
есть круг
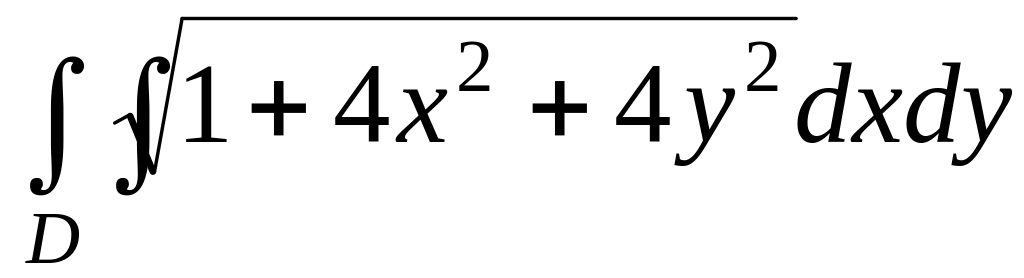 ,
где D
есть круг
,
где D
есть круг
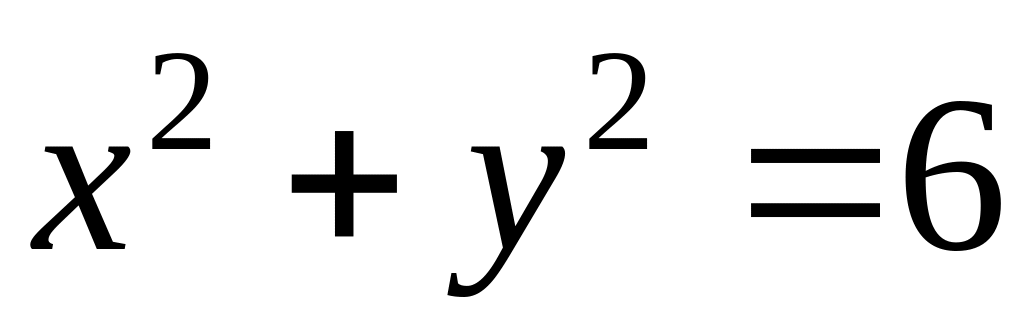
Задание
№6. Вычислить
работу, совершаемую переменной силой
![]() на криволинейном пути L,
соединяющем заданные точки M
и
N
на криволинейном пути L,
соединяющем заданные точки M
и
N
 ,
где L
– дуга параболы
,
где L
– дуга параболы
 ;
M(0,0); N(1,3)
;
M(0,0); N(1,3) ,
где L
– дуга параболы
,
где L
– дуга параболы
 ;
M(0,1); N(2,9)
;
M(0,1); N(2,9) ,
где L
– дуга параболы
,
где L
– дуга параболы
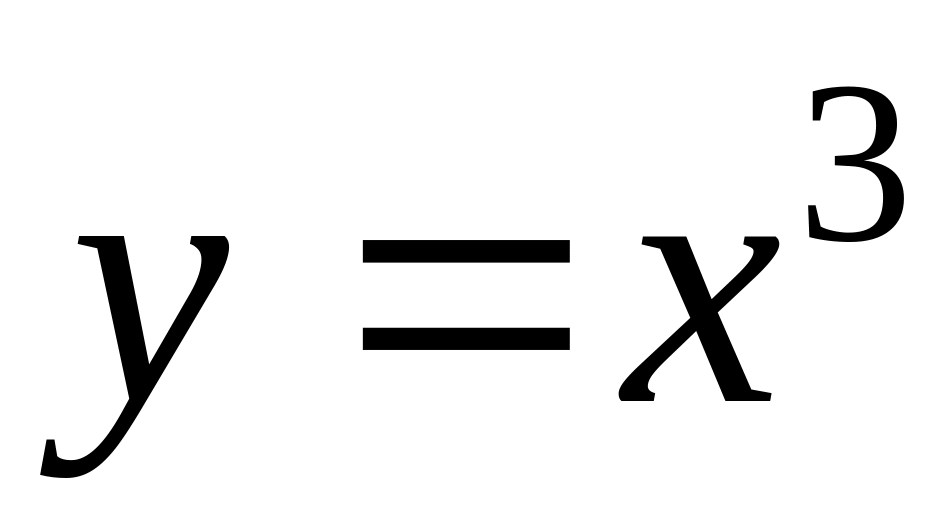 ;
M(0,0); N(2,8)
;
M(0,0); N(2,8) ,
где L
– дуга параболы
,
где L
– дуга параболы
 ;
M(0,0); N(2,32)
;
M(0,0); N(2,32) ,
где L – дуга
параболы
,
где L – дуга
параболы
 ,
М(1;4); N(
3;30)
,
М(1;4); N(
3;30) ,
где L – отрезок
прямой, соединяющей точки M(1;2)
и N(3;3)
,
где L – отрезок
прямой, соединяющей точки M(1;2)
и N(3;3) ,
где L
– дуга кубической параболы
,
где L
– дуга кубической параболы
 ,
М(0;1), N(1;2)
,
М(0;1), N(1;2) ,
где L
– дуга кубической параболы
,
где L
– дуга кубической параболы
 ,
М(1;3), N(2;10)
,
М(1;3), N(2;10) ,
где L – дуга
параболы
,
где L – дуга
параболы
 ,
М(1;2); N(
3;12)
,
М(1;2); N(
3;12) ,
где L – дуга
параболы
,
где L – дуга
параболы
 ,
М(2;14), N(
3;29)
,
М(2;14), N(
3;29) ,
где L – дуга
параболы
,
М(1;4); N(
2;14)
,
где L – дуга
параболы
,
М(1;4); N(
2;14)
Решение типовых заданий
Построить на плоскости XOY область интегрирования. Изменить порядок интегрирования и вычислить двукратный интеграл при заданном и измененном порядках интегрирования
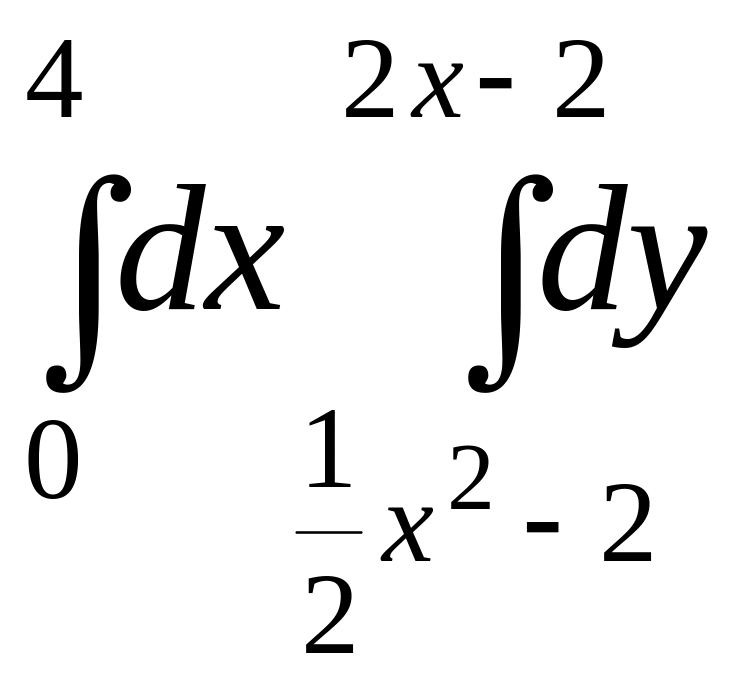
Область
интегрирования D
ограничена линиями x=0;
x=4;
![]() ;
;
![]() .
Построим в одной системе координат все
линии: x=0
– ось
(Oy);
x=4 – прямая
параллельна оси (Oy)
и проходящая через точку (4;0);
- парабола (строим по точкам, т.е. с учетом
таблицы)
.
Построим в одной системе координат все
линии: x=0
– ось
(Oy);
x=4 – прямая
параллельна оси (Oy)
и проходящая через точку (4;0);
- парабола (строим по точкам, т.е. с учетом
таблицы)
X |
0 |
1 |
2 |
3 |
4 |
Y |
-2 |
-1,5 |
0 |
2,5 |
6 |
- прямая для построения которой достаточно взять две точки
|
0 |
4 |
Y |
-2 |
6 |
Вычислим заданный двукратный интеграл, причем вычисление начинаем с внутреннего интеграла
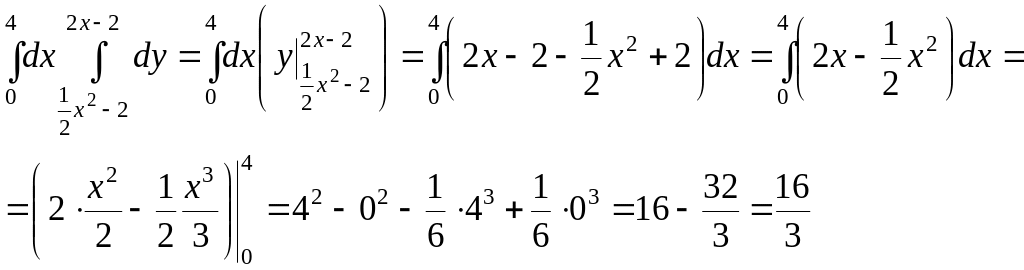
Изменим порядок интегрирования: теперь внешней будет переменная y, а внутренней - переменная x.
Внешняя переменная y меняется в пределах от (-2) до 6.
Для
определения пределов внутренней
переменной x
движемся
слева направо параллельно оси (OX).
На входе в область пересекаем прямую
, отсюда
![]() - нижний предел внутреннего интеграла.
На выходе из области пересекаем параболу
,
отсюда
- нижний предел внутреннего интеграла.
На выходе из области пересекаем параболу
,
отсюда
![]() .
Таким образом, получим двукратный
интеграл
.
Таким образом, получим двукратный
интеграл
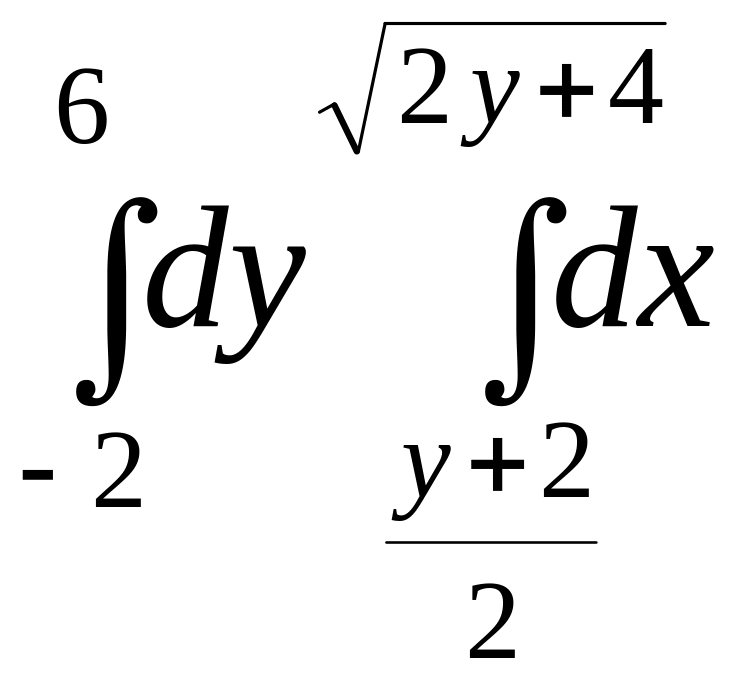 .
.
Вычислим
полученный интеграл


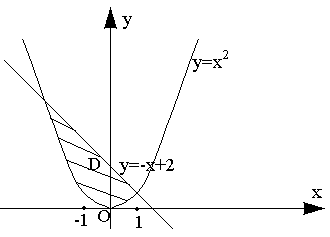
Вычислить площадь фигуры ограниченной линиями ;

Решение.
Построим фигуру, площадь которой нужно вычислить, для этого в прямоугольной системе координат начертим параболу и прямую .

 X
X