- •Кафедра высшей математики сборник контрольных работ и индивидуальных заданий по высшей математике
- •Индивидуальное задание № 1 по теме «Аналитическая геометрия на плоскости.»
- •Пример 2. В полярной системе координат построить график функции (без исследования). Записать уравнение, построенной кривой в декартовых координатах.
- •Индивидуальное задание № 4 по теме: Определенный интеграл.
- •Индивидуальное задание № 5 по теме “ Кратные интегралы и их приложения ”
- •Задание №2: Вычислить площадь фигуры, ограниченной линиями
- •Задание №4: Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями.
- •Итак, нам нужно найти площадь области d . Как известно .
- •Индивидуальное задание №7
- •Контрольная работа №2 по теме “ Вычисление пределов”.
- •Контрольная работа №3
- •Вариант 1
- •Вариант 1
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ
Кафедра высшей математики сборник контрольных работ и индивидуальных заданий по высшей математике
Пособие для студентов инженерных специальностей АГАУ



Барнаул 2002
УДК
Абакумова Н.А.,Зенков А.В., Кокшарова М.В, Колесникова Т.Г., Морозова С.В. Сборник контрольных работ и индивидуальных заданий по высшей математике - Барнаул: Изд-во АГАУ 2002 - с.
Программа по высшей математике для студентов инженерных специальностей предусматривает выполнение ряда индивидуальных заданий и контрольных работ.
Настоящий сборник содержит по 30 вариантов индивидуальных заданий по темам, причем подробно рассматривается решение одного из вариантов по каждому разделу. Также в сборник включены контрольные работы по основным разделам курса высшей математики.
Утверждено методическим советом ИТАИ. Протокол № от
Рецензент: к.ф.-м.н.И.В.Лёвкин
Индивидуальное задание № 1 по теме «Аналитическая геометрия на плоскости.»
В задачах 1 – 30 даны координаты вершин треугольника АВС. Найти:
1)длину стороны АВ;
2) уравнения сторон АВ и ВС и их угловые коэффициенты;
3) угол В в радианах с точностью до двух знаков;
4) уравнение высоты СД и её длину;
5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СД;
6) уравнение прямой, проходящей через точку К параллельно стороне АВ;
7) координаты точки М, расположенной симметрично точке А относительно прямой СД.
№ 1 А(-2;2), В(10;-7), С(14;15).
№ 2 А(-4;-1), В(8;-10), С(12;12).
№ 3 А(-7;1), В(5;-8), С(9;14).
№ 4 А(1;2), В(13;-7), С(17;15).
№ 5 А(-7;-1), В(-5;-10), С(9;12).
№ 6 А(0;3), В(12;-6), С(16;16).
№ 7 А(-8;4), В(4;-5), С(8;17).
№ 8 А(-2;2), В(10;-7), С(14;15).
№ 9 А(-3;0), В(9;-9), С(13;13).
№10 А(-6;-2), В(6;-11), С(10;11).
№11 А(-8;-3), В(4;-12), С(8;10).
№12 А(-5;7), В(7;-2), С(11;20).
№13 А(-12;-1), В(0;-10), С(4;12).
№14 А(-10;9), В(2;0), С(6;22).
№15 А(0;2), В(12;-7), С(16;15).
№16 А(-9;6), В(3;-3), С(7;19)
№17 А(1;0), В(13;-9), С(17;13),
№18 А(-4;10), В(8;1), С(12;23),
№19 А(2;5), В(14;-4), С(18;18),
№20 А(-1;4), В(11;-5), С(15;17),
№21 А(-2;7), В(10;-2), С(8;12),
№22 А(-6;8), В(6;-1), С(4;13),
№23 А(3;6), В(15;-3), С(13;11),
№24 А(-10;5), В(2;-4), С(0;10),
№25 А(-4;12), В(8;3), С(6;17),
№26 А(-3;10), В(9;1), С(7;15),
№27 А(4;1), В(16;-8), С(14;6),
№28 А(-7;4), В(5;-5), С(3;9),
№29 А(0;3), В(12;-6), С(10;8),
№30 А(-5;9), В(7;0), С(5;14).
Задание № 2. Какую линию определяет уравнение в задачах
1 – 30. Построить данную линию в декартовой системе координат.
№ 1) 2х2 – 4х + 2у – 3 = 0
№ 2) 2х2 + 5у2 – 12х + 10у + 13 = 0
№ 3) х2 - у2 + 6х + 4у – 4 = 0
№ 4) 4х2 + 9у2 – 24х + 36у + 36 = 0
№ 5) х2 – у2 – 4х – 6у – 9 = 0
№ 6) у2 – 10х – 2у – 19 = 0
№ 7) х2 – у2 + 4х + 2у – 6 = 0
№ 8) 2х2 + 5у2 – 8х – 2 = 0
№ 9 у2 – 6х + 14у + 49 = 0
№ 10) 16х2 +25у2 – 32х + 50у – 359 = 0
№ 11)
![]() х2
-
х2
-
![]() у2
– х +
у2
– х +
![]() у
– 1 = 0
у
– 1 = 0
№ 12) х2 – 6х – 4у + 29 = 0
№ 13) 4х2 + 9у2 + 72х + 108 = 0
№ 14) 9х2 – 25у2 – 18х – 100у – 316 =0
№ 15) 4у2 – 6у – х + 11 = 0
№ 16) х2 – у2 – 2х – 3 = 0
№ 17) у2 + 4у – 6х + 7 = 0
№ 18) х2 + у2 – 2х + 4у –20 = 0
№ 19) 5х2 – 6у2 + 10х – 12у – 31 = 0
№ 20) 2х2 + 4у2 – 4х + 8у –10 = 0
№ 21) у2 + 8у – 2х + 10 = 0
№ 22) х2 – 2у2 – 2х + 8у – 17 = 0
№ 23) х2 + 4у2 + 4х – 24у + 36 = 0
№ 24) у2 – 4у + х – 6 = 0
№ 25) х2 – у2 – 4х + 2у – 4 = 0
№ 26) 2х2 + 3у2 – 4х + 6у – 7 = 0
№ 27) х2 –6х + у – 7 = 0
№ 28) х2 – 4у2 – 2х + 16у + 1 = 0
№ 29) 4х2 + 4у2 + 3у – 2 = 0
№ 30) х2 – 4у2 + 6х + 5 = 0
Решение типовых заданий:
Пример 1
Даны вершины треугольника АВС: А(-3;3), В(9;-6), С(7;8).
Найти: 1) длину стороны АВ;
уравнение сторон АВ и ВС и их угловые коэффициенты;
угол В в радианах;
уравнение высоты СД и её длину;
уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СД;
уравнение прямой, проходящей через точку К параллельно стороне АВ;
координаты точки М, расположенной симметрично точке А относительно прямой СД.
Решение.
1)
Расстояние
![]() между точками А(х1;у1)
и В(х2;у2)
определяется по формуле
между точками А(х1;у1)
и В(х2;у2)
определяется по формуле
![]() Применяя данную формулу, вычислим длину
стороны АВ:
Применяя данную формулу, вычислим длину
стороны АВ:
![]()
2)
Уравнение прямой, проходящей через
две данные точки А(х1;у1)
и В(х2;у2),
имеет вид:
![]() .
Подставляя в формулу координаты точек
А и В, получим уравнение стороны АВ:
.
Подставляя в формулу координаты точек
А и В, получим уравнение стороны АВ:
![]() ,
или
,
или
![]() ;
12у – 36 = - 9х – 27.
;
12у – 36 = - 9х – 27.
Таким образом, общее уравнение прямой АВ имеет вид:
3х + 4у – 3 = 0.
Решив
последнее уравнение относительно у,
определим уравнение стороны АВ в виде
уравнения прямой с угловым коэффициентом:
![]() ,
откуда kАВ
=
,
откуда kАВ
=
![]() .
.
Аналогично
определим уравнение стороны ВС и её
угловой коэффициент:![]() ;
;
![]() ;
- 2у- 12 = 14х – 126;
;
- 2у- 12 = 14х – 126;
7х + у – 57 = 0 – общее уравнение прямой ВС,
у = -7х + 57, откуда kВС = -7.
3)
Тангенс угла
![]() между двумя прямыми, угловые коэффициенты
которых k1
и
k2
вычисляется по формуле
между двумя прямыми, угловые коэффициенты
которых k1
и
k2
вычисляется по формуле
![]() .
Искомый угол В образован прямыми АВ и
ВС, угловые коэффициенты которых
найдены: kAB=
.
Искомый угол В образован прямыми АВ и
ВС, угловые коэффициенты которых
найдены: kAB=
![]() ;
kBC=
;
kBC=
![]() ,
тогда
,
тогда
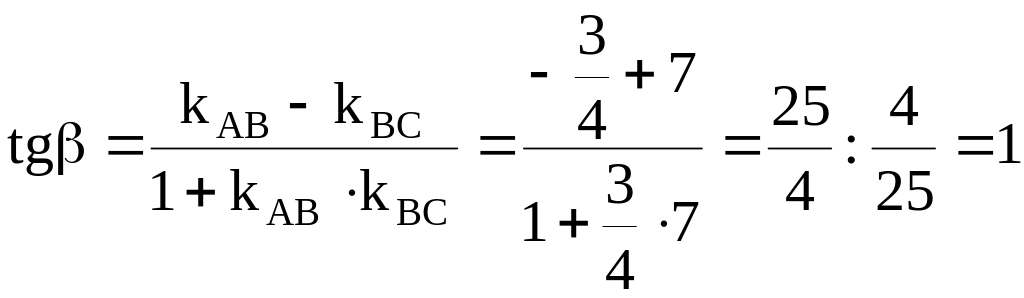 .
.
![]() рад.
рад.
4)
Так как высота CД
перпендикулярна стороне AB,
то угловые коэффициенты этих прямых
обратны по величине и пртивоположны
по знаку, т.е.
kCД=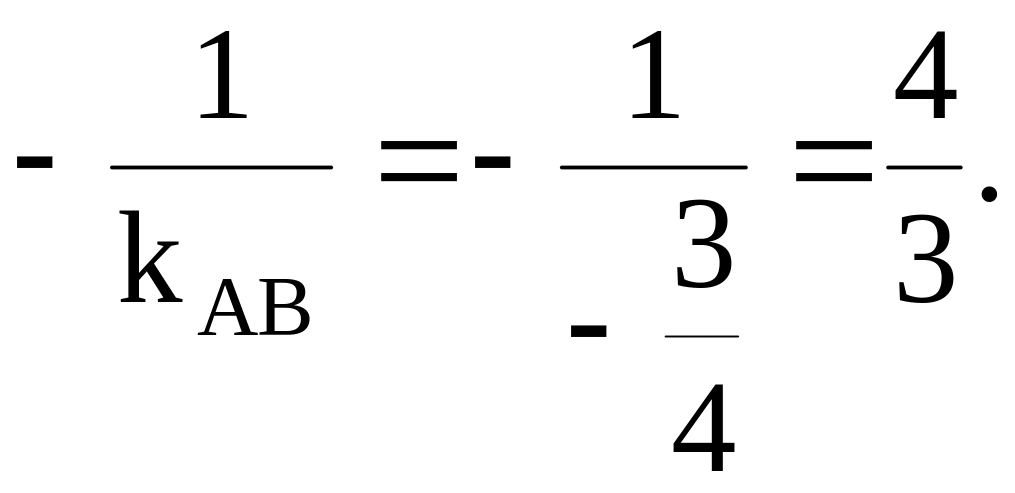
Уравнение прямой проходящей через данную точку (х1;у1) в заданном угловым коэффициентом направлении, имеет вид:
у – у1
= k(х – х1)
. Подставим координаты точки С и
kCД=
![]() ,
получим уравнение высоты CД: у – 8 =
,
получим уравнение высоты CД: у – 8 =
![]() ,
3у – 24 = 4х – 28, 4х – 3у – 4 = 0 – общее
уравнение высоты CД. Для
нахождения длины CД, вычислим координаты
точки Д пересечения прямых АВ и CД, для
этого решим систему из уравнений
определяющих указанные прямые:
,
3у – 24 = 4х – 28, 4х – 3у – 4 = 0 – общее
уравнение высоты CД. Для
нахождения длины CД, вычислим координаты
точки Д пересечения прямых АВ и CД, для
этого решим систему из уравнений
определяющих указанные прямые:![]() .
Решим систему уравнений методом Крамера,
для чего вычислим определители:
.
Решим систему уравнений методом Крамера,
для чего вычислим определители:
Δ
=
![]() = - 25; Δх
=
= - 25; Δу
=
= - 25; Δх
=
= - 25; Δу
=
![]() = 0;
= 0;
Тогда
решение системы имеет вид:
![]() ;
;
![]() ,
то есть положение точки Д определяется
координатами (1;0). Вычислим длину высоты
,
то есть положение точки Д определяется
координатами (1;0). Вычислим длину высоты
![]()
5) Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:
![]()
Следовательно,
![]()
![]() то есть Е(8;1).
то есть Е(8;1).
Подставив в формулу уравнения прямой, проходящей через две данные точки, координаты точек А и Е, определяем уравнение медианы АЕ.
![]()
![]()
![]()
таким образом, 2х + 11у – 27 = 0 есть общее уравнение медианы АЕ.
Чтобы определить координаты точки пересечения высоты CД и медианы АЕ, решим систему уравнений, задающих указанные прямые.
![]()
![]()
![]() ;
решая данную систему уравнений методом
Крамера, вычислим Δ = 50, Δх
= 125, Δу
= 100, тогда
;
решая данную систему уравнений методом
Крамера, вычислим Δ = 50, Δх
= 125, Δу
= 100, тогда
![]() ;
;
![]() ,
то есть К(2,5;2) – точка пересечения высоты
CD
и медианы АЕ.
,
то есть К(2,5;2) – точка пересечения высоты
CD
и медианы АЕ.
6)
Так как искомая прямая параллельна
стороне АВ, то её угловой коэффициент
будет равен угловому коэффициенту
прямой АВ, то есть
![]() .
Применяя формулу нахождения уравнения
прямой, проходящей через данную точку
в заданном направлении, получаем:
.
Применяя формулу нахождения уравнения
прямой, проходящей через данную точку
в заданном направлении, получаем:
![]() или
или
![]() - общее уравнение искомой прямой.
- общее уравнение искомой прямой.
7) Так как прямая АВ перпендикулярна прямой CД, то искомая точка М, расположенная симметрично точке А относительно прямой CД лежит на прямой АВ. Кроме того, точка Д является серединой отрезка АМ. Применяя формулы деления отрезка на две равные части, вычисляем координаты точки М:
![]() ,
отсюда хМ
=
5;
,
отсюда хМ
=
5;
![]() ,
отсюда уМ=
- 3.
,
отсюда уМ=
- 3.
То есть точка М имеет координаты (5;-3).
Т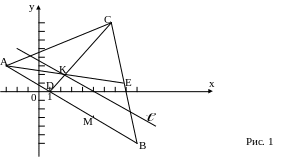 реугольник
АВС, высота CД,
медиана АЕ, прямая
реугольник
АВС, высота CД,
медиана АЕ, прямая
![]() , точка М построены в системе координат
хОу на рисунке 1.
, точка М построены в системе координат
хОу на рисунке 1.
Пример 2 Какую линию определяет уравнение 4х2+9у2+8х-36у+4=0. Построить данную линию в декартовой системе координат.
Решение. Сгруппируем слагаемые, содержащие х и у:
4х2+9у2+8х-36у+4=0.
(4х2+8х)+(9у2-36у)+4=0.
Вынесем за скобки из первого выражения 4, из второго – 9. Получим 4(х2+2х)+9(у2-4у)+4=0. В скобках добавим слагаемые, так чтобы получить формулу квадрата разности или квадрата суммы. Для того, чтобы равенство не изменилось, вычтем эти слагаемые после скобок.
4(х2+2х+1)+9(у2-4у+4)-4-36+4=0
4(х+1)2+9(у-2)2=36.
Поделим обе части равенства на 36, в результате получим:
![]()
Данное уравнение определяет эллипс, вершина которого находится в точке С(-1,2), при этом а2=9, следовательно а=3 и в2=4, следовательно в=2. Указанный эллипс построен в прямоугольной системе координат хОу на рисунке 2

Индивидуальное задание № 2
по теме «Приложение векторной алгебры к решению
задач математики.»
В задачах 1 – 30 указаны координаты вершин пирамиды АВСД. Требуется:
записать векторы
 в системе орт и вычислить модули этих
векторов;
в системе орт и вычислить модули этих
векторов;определить угол между векторами
 ;
;определить проекцию вектора
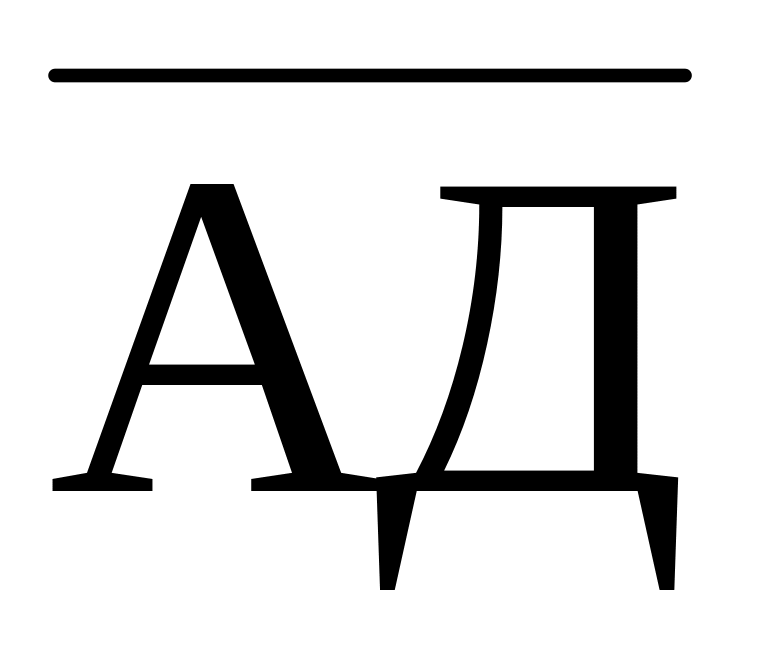 на вектор
на вектор
 ;
;вычислить площадь грани АВС;
вычислить объём пирамиды АВСД и длину высоты ДН.
1) А(3;1;1), В(7;5;-1), С(5;12;-9), Д(3;3;2);
2) А(4;-1;-1), В(8;3;-3), С(6;10;-11), Д(4;1;0);
3) А(2;-3;2), В(6;1;0), С(4;8;-8), Д(2;-1;3);
4) А(-2;2;0), В(2;6;-2), С(0;13;-10), Д(-2;4;1);
5) А(5;-2;4), В(9;2;2), С(7;9;-6), Д(5;0;5);
6) А(2;-3;1), В(6;1;-1), С(4;8;-9), Д(2;-1;2);
7) А(5;-1;-4), В(9;3;-6), С(7;10;-14), Д(5;1;-3);
8) А(1;-4;0), В(5;0;-2), С(3;7;-10), Д(1;-2;1);
9) А(-3;-6;2), В(1;-2;0), С(-1;5;-8), Д(-3;-4;3);
10) А(-1;1;-5), В(3;5;-7), С(1;12;-15), Д(-1;3;-4);
11) А(-4;2;-1), В(0;6;-3), С(-2;13;-11), Д(-4;4;0);
12) А(0;4;3), В(4;8;1), С(2;15;-7), Д(0;6;4);
13) А(-2;0;-2), В(2;4;-4), С(0;11;-12), Д(-2;2;-1);
14) А(3;3;-3), В(7;7;-5), С(5;14;-13), Д(3;5;-2);
15) А(4;-2;5), В(8;2;3), С(6;9;-5), Д(4;0;6);
16) А(-5;0;1), В(-4;-2;3), С(6;2;11), Д(3;4;9);
17) А(1;-4;0), В(2;-6;2), С(12;-2;10), Д(9;0;8);
18) А(-1;-2;-8), В(0;-4;-6), С(10;0;2), Д(7;2;0);
19) А(0;2;-10), В(1;0;-8), С(11;4;0), Д(8;6;-2);
20) А(3;1;-2), В(4;-1;0), С(14;3;8), Д(11;5;6);
21) А(-8;3;-1), В(-7;1;1), С(3;5;9), Д(0;7;7);
22) А(2;-1;-4), В(3;-3;-2), С(13;1;6), Д(10;3;4);
23) А(-4;5;-5), В(-3;3;-3), С(7;7;5), Д(4;9;3);
24) А(-2;-3;2), В(-1;-5;4), С(9;-1;12), Д(6;1;10);
25) А(-3;4;-3), В(-2;2;-1), С(8;6;7), Д(5;8;5);
26) А(-5;2;-4), В(-4;0;-2), С(6;4;6), Д(3;6;4);
27) А(-7;3;1), В(-6;1;3), С(4;5;11), Д(1;7;9);
28) А(-6;-4;-3), В(-5;-6;-1), С(5;-2;7), Д(2;0;5);
29) А(-1;-3;3), В(0;-5;5), С(10;-1;13), Д(7;1;11);
30) А(4;-1;-2), В(5;-3;0), С(15;1;8), Д(12;3;6);
Пример. Даны координаты вершин пирамиды АВСД:
А(0;1;3), В(1;-1;5), С(11;3;13), Д(-2;1;7).
Требуется:
1) записать векторы
в системе орт
![]() и найти модули этих векторов;
и найти модули этих векторов;
2) определить угол между векторами ;
3)
найти проекцию вектора
на вектор
![]() ;
;
4) вычислить площадь грани АВС;
вычислить объём пирамиды АВСД и длину высоты ДН.
Решение:
Произвольный вектор
![]() с координатами (ах;ау;аz)
может быть представлен в системе орт
с координатами (ах;ау;аz)
может быть представлен в системе орт
![]() следующей формулой:
следующей формулой:
![]() Если даны точки М1(x1;y1;z1)
и
M2(x2;y2;z2),
то координаты вектора
Если даны точки М1(x1;y1;z1)
и
M2(x2;y2;z2),
то координаты вектора
![]() находятся по формулам: ax=
x2-x1,
ay=
y2-y1,
az=
z2-z1.
находятся по формулам: ax=
x2-x1,
ay=
y2-y1,
az=
z2-z1.
Представим
векторы
![]() и
в системе орт
следующим образом:
и
в системе орт
следующим образом:
![]()
Модуль
вектора
![]() вычисляется по формуле:
вычисляется по формуле:![]() .
Найдем модули векторов
.
Найдем модули векторов
![]() и
:
и
:
![]() .
.
2)
Косинус угла между двумя векторами
равен скалярному произведению этих
векторов, делённому на произведение
их модулей:
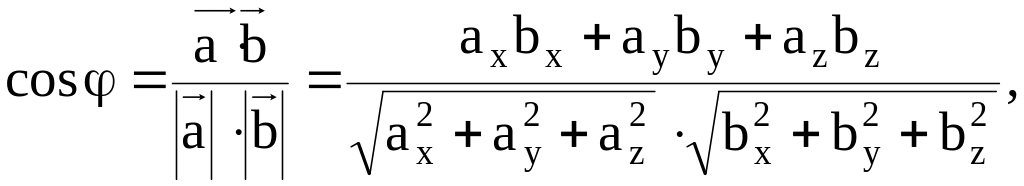 где
где![]() .
.
Тогда
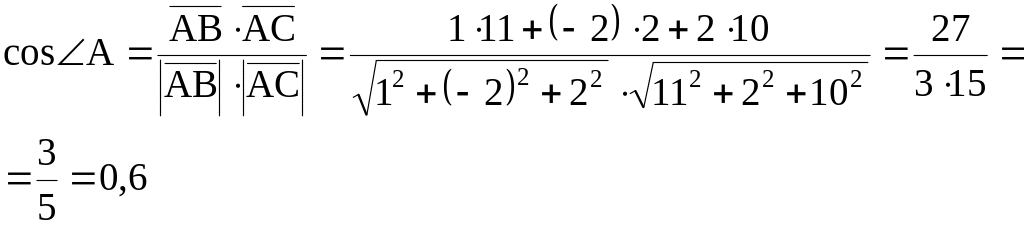
![]()
3)
Проекция вектора
![]() на
вектор
на
вектор
![]() равна скалярному произведению этих
векторов, деленному на модуль этих
вектора
равна скалярному произведению этих
векторов, деленному на модуль этих
вектора
![]() ,
т.е.
,
т.е.
![]()
В нашем случае получим
![]()
4)
Пусть
вектор
![]() есть векторное произведение вектора
на
вектор
.
Тогда модуль вектора
есть векторное произведение вектора
на
вектор
.
Тогда модуль вектора
![]() выражает собой площадь параллелограмма,
построенного на векторах
и
,
а площадь треугольника, построенного
на этих векторах, равна половине модуля
вектора
.
выражает собой площадь параллелограмма,
построенного на векторах
и
,
а площадь треугольника, построенного
на этих векторах, равна половине модуля
вектора
.
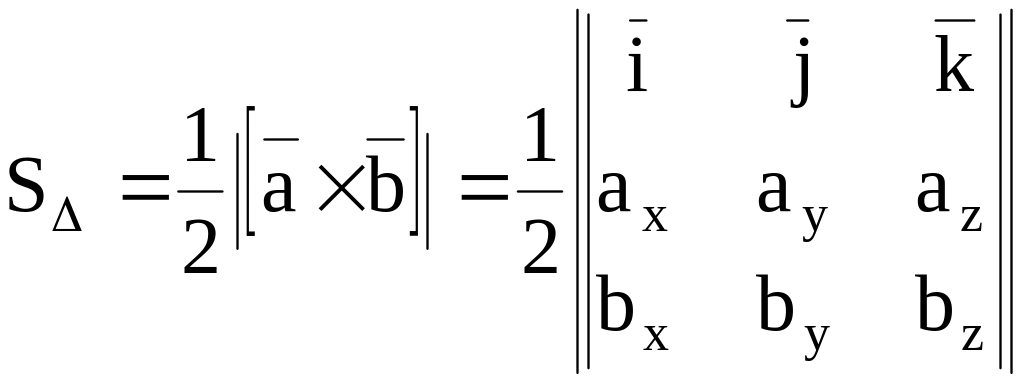
Таким
образом, площадь грани ABC
равна
половине модуля векторного произведения
векторов
![]() и
и
![]() .
.
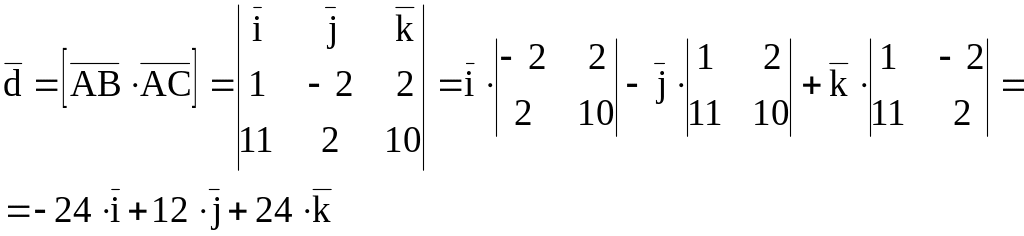
Итак,
вектор
![]() .
.
Найдём![]() :
:
![]()
![]()
5)
Объём параллелепипеда, построенного
на трёх некомпланарных векторах, равен
абсолютной величине их смешанного
произведения. Из школьного курса
геометрии известно, что объём пирамиды
равен
![]() объёма
параллелепипеда:
объёма
параллелепипеда:
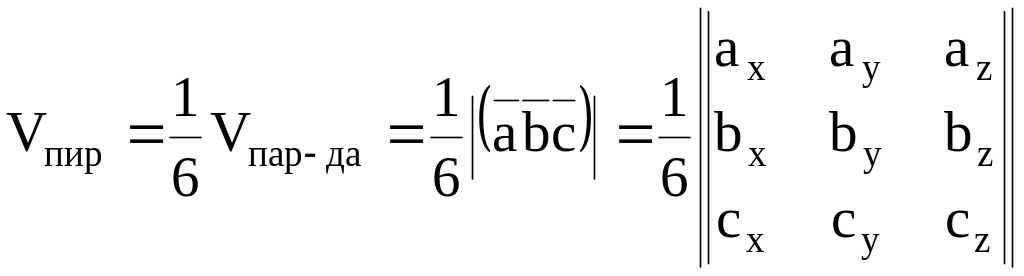
Вычислим смешанное произведение трёх некомпланарных векторов , и :
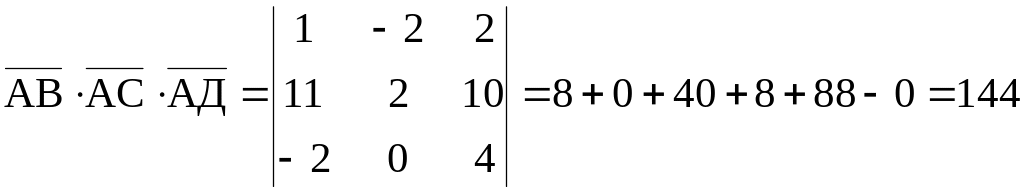
Следовательно
![]() .
.
Для
того чтобы найти длину высоты
![]() воспользуемся
формулой из школьного курса геометрии
воспользуемся
формулой из школьного курса геометрии
![]() ,
,
![]() .
.
Таким
образом
![]() .
.
Иначе высоту h можно вычислить таким образом: высота есть модуль проекции вектора на вектор , получившийся в результате векторного произведения векторов и :
![]() ,
где
,
где
![]()
![]() .
.
Ответ:
1)
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]()
2)
3)
![]()
4)
![]()
5)![]() ,
,
![]()
Индивидуальное задание №3
по теме «Применение производной к исследованию
функций и построению их графиков
»
1.Исследовать функции и построить их графики.
1) а) y
= 2x2-x4
б)
![]()
2) а) y = (x+3)3 б) y = ln(1+x2)
3) a) y = 2x3-3x2+7 б) y=xe-x
4) a)
![]() б)
б)
![]()
5) a)
![]() б)
б)
![]()
6) a)
![]() б)
б)
![]()
7) a)
![]() б)
б)
![]()
8) a)
![]() б)
б)
![]()
9) a)
![]() б)
б)
![]()
10) a)
y=x3-6x2+9x-5
б)
![]()
11) a)
![]() б)
б)
![]()
12) a)
![]() б)
б)
![]()
13) a)
![]() б)
б)
![]()
14) a)
![]() б)
б)
![]()
15) a)
![]() б)
б)
![]()
16) a)
![]() б)
б)
![]()
17) a)
![]() б)
б)
![]()
18) a)
![]() б)
б)
![]()
19) a)
б)
![]()
20) a)
![]() б)
б)
![]()
21) a)
![]() б)
б)
![]()
22) a)
y=x3+3x2-12x+5
б)
![]()
23) a)
![]() б)
б)
![]()
24) a)
y=x3+3x2-12x+5
б)
![]()
25) a)
![]() б)
б)
![]()
26) a)
y=2x3-15x2+26x-32
б)
![]()
27) a)
![]() б)
б)
![]()
28) a)
y=x3+9x2+24x+17
б)
![]()
29) a)
![]() б)
б)
![]()
2. В полярных координатах построить график функции.
Записать уравнение построенной кривой в декартовых координатах.
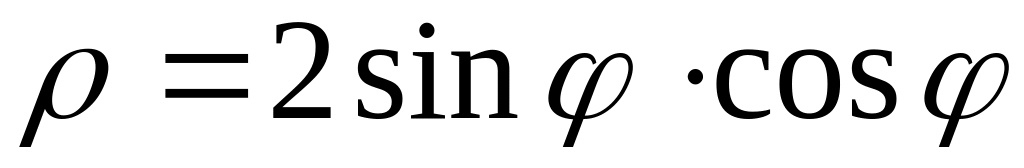 16)
16)
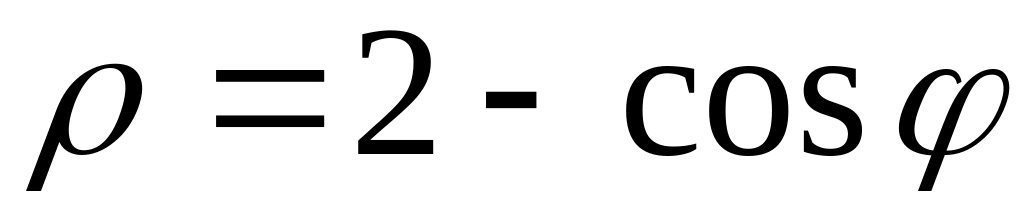
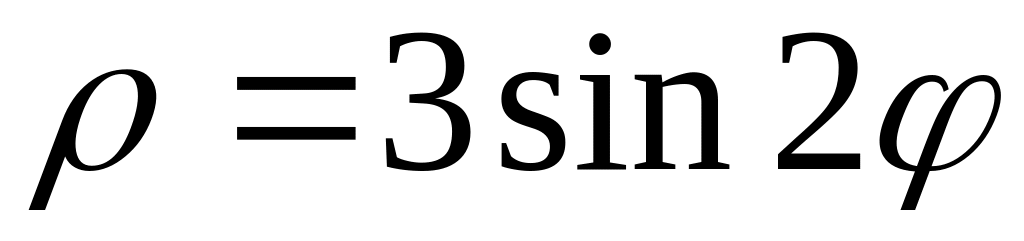 17)
17)
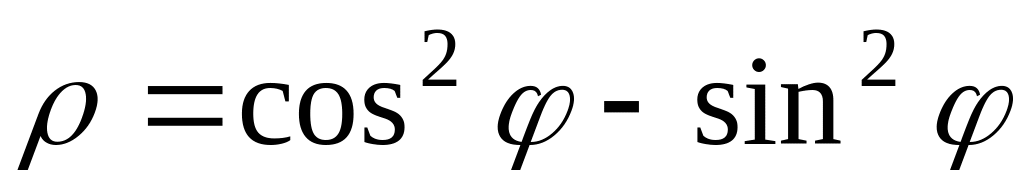
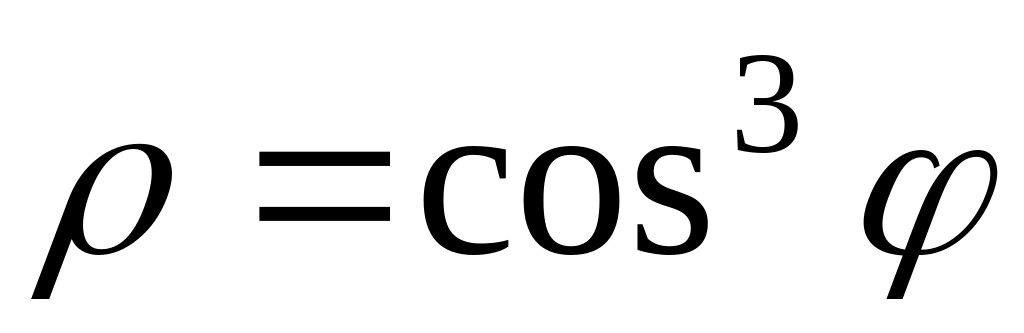 18)
18)

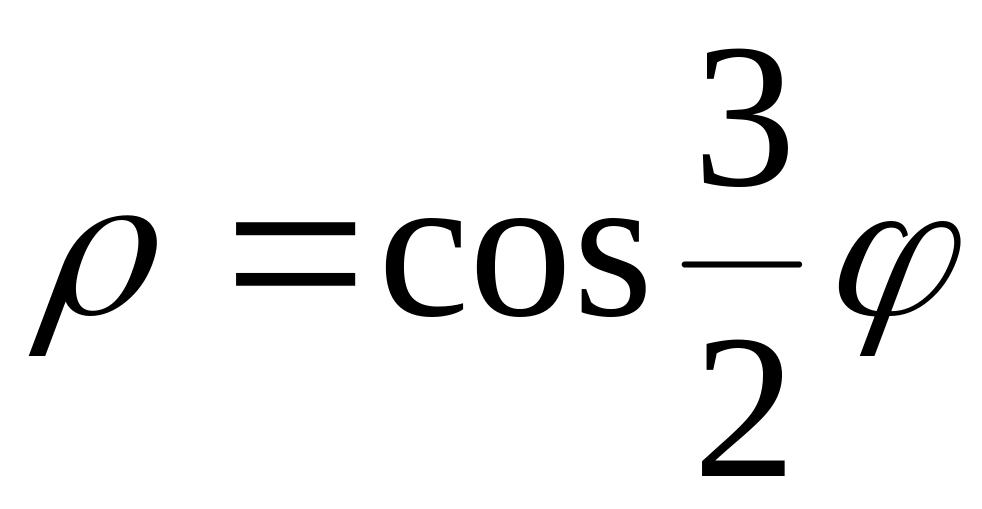 19)
19)
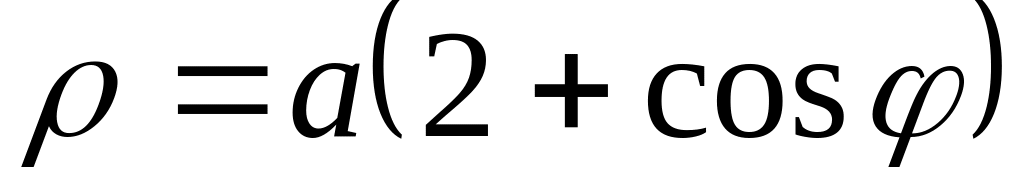
20)

 21)
21)
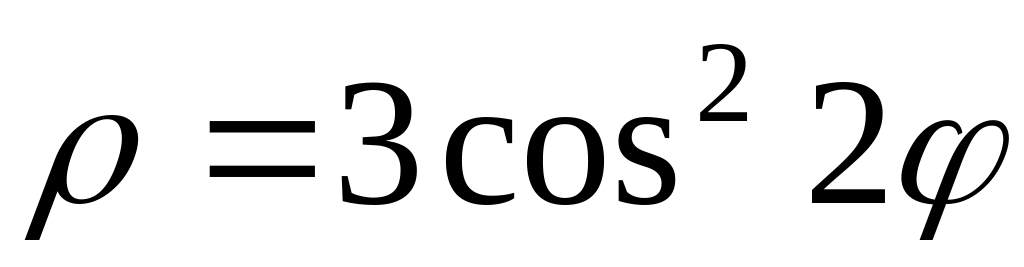
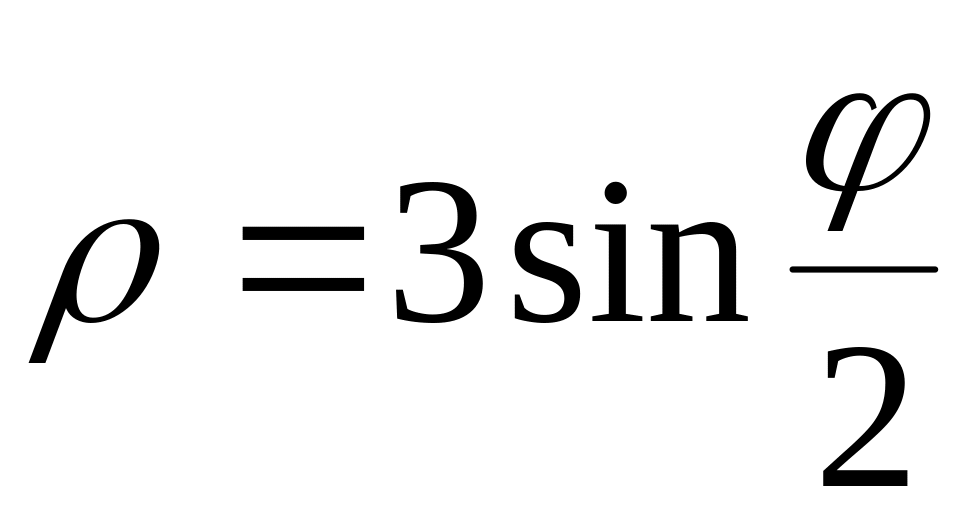 22)
22)
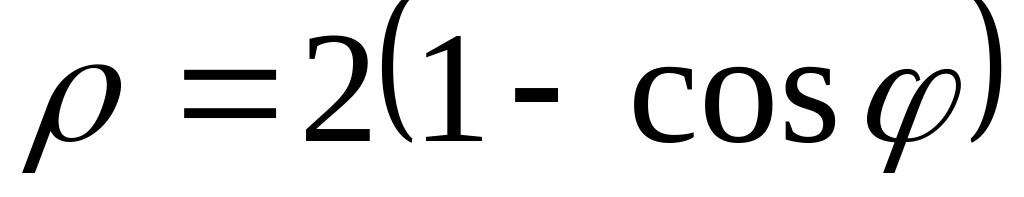
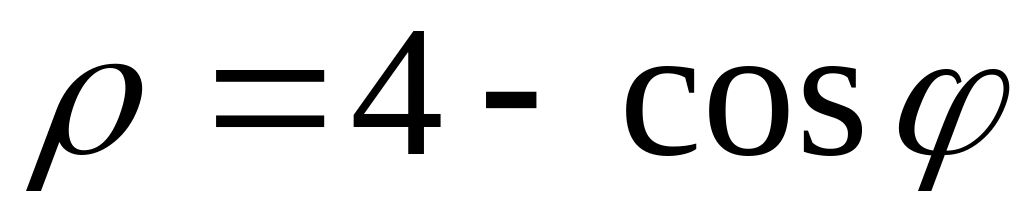 23)
23)
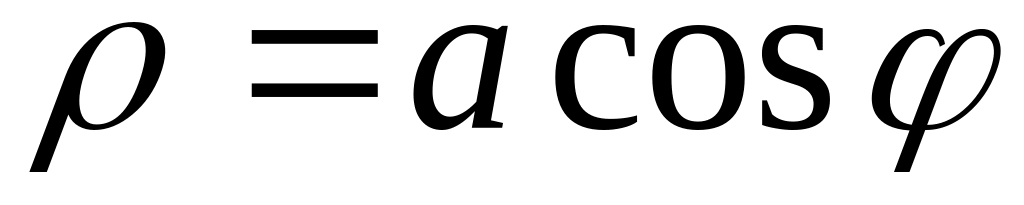
 24)
24)
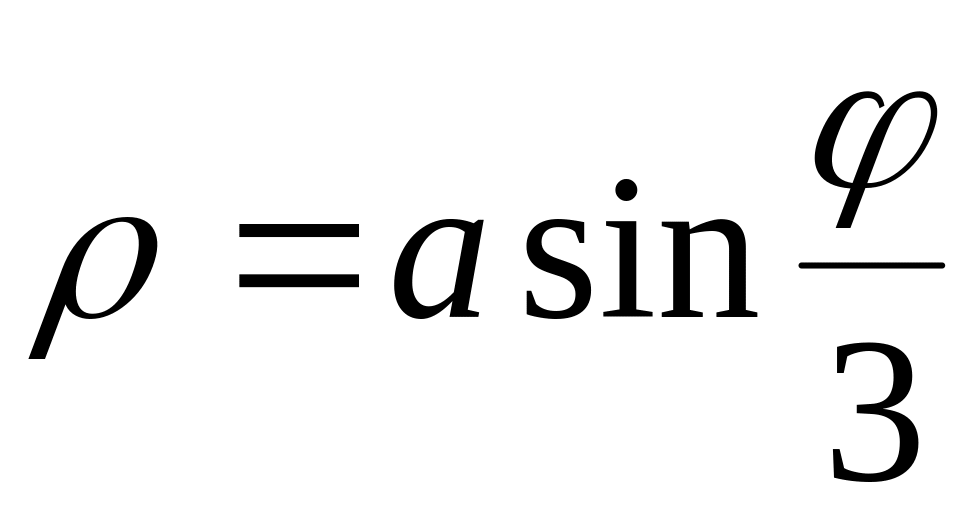
10)![]() 25)
25)
![]()
11)![]() 26)
26)
![]()
12)
![]() 27)
27)
![]()
13)
![]() 28)
28)
![]()
14)
![]() 29)
29)
![]()
15)
![]() 30)
30)
![]()
3. Решить задачу.
Канал, ширина которого 27м, под прямым углом впадает в другой канал шириной 64м. Какова длина брёвен, которые можно сплавлять по этой системе каналов?
Найти наибольший объём цилиндра, у которого полная поверхность равна 24πм2.
Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения равен 18м. При каком радиусе полукруга площадь сечения будет наибольшей?
Из точек A и B по указанным стрелками направлениям выходят одновременно пароход и яхта. Их скорости соответственно: 40км/ч и 16км/ч. Через сколько времени расстояние между ними окажется наименьшим, если AB=145км?
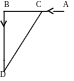
Вблизи завода A проводится по намеченной прямой к городу железная дорога. Под каким углом α к проектируемой железной дороге нужно провести шоссе с завода A, чтобы доставка грузов из A в B была наиболее дешевой, если стоимость перевозки 1 тонны-километра по шоссе в m раз дороже, чем по железной дороге.

Бревно длиной 20м имеет форму усеченного конуса, диаметры основания которого равны соответственно 2 и 1 м. Требуется вырубить из бревна балку с квадратным сечением, ось которой совпадала бы с осью бревна и объем которой был бы наибольшим. Каковы должны быть размеры балки?
Населенные пункты A и B расположены по одну сторону от реки. Через реку намечено построить мост. В каком месте следует возвести этот мост, чтобы сумма расстояний от пунктов A и B до моста была наименьшей.

Три пункта A, B и С расположены так, что
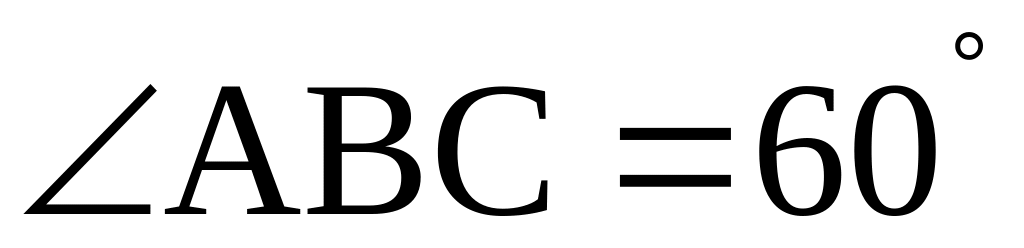 .
Из пункта А выходит автомобиль, из B
–одновременно
поезд. Автомобиль движется по направлению
к B
со скоростью
80 км/ч, поезд движется по направлению
к C
со скоростью
50 км/ч. В какой момент времени (от начала
движения) расстояние между поездом и
автомобилем будет наименьшим, если
AB=200км?
.
Из пункта А выходит автомобиль, из B
–одновременно
поезд. Автомобиль движется по направлению
к B
со скоростью
80 км/ч, поезд движется по направлению
к C
со скоростью
50 км/ч. В какой момент времени (от начала
движения) расстояние между поездом и
автомобилем будет наименьшим, если
AB=200км?
9)
Два самолета летят в одной плоскости
и прямолинейно под углом в
![]() с
одинаковой скоростью v
км/ч. В
некоторый момент один
с
одинаковой скоростью v
км/ч. В
некоторый момент один
самолет пришел в точку пересечения линии движения, а второй не дошел до неё а км. Через сколько времени расстояние между самолетами будет наименьшим и чему равно это расстояние?
Кровельщик делает открытый желоб наименьшей вместительности, у которого дно и бока были бы шириной 10 см и бока одинаково наклонены ко дну. Какова должна быть ширина желоба наверху?
Требуется построить котел, состоящий из цилиндра, завершенного двумя полусферами, со стенками постоянной толщины так, чтобы при данном объеме V он имел бы наименьшую поверхность.
Из листа, имеющего форму круга радиуса R, вырезать такой сектор, чтобы, свернув его, получить воронку наибольшей вместительности.
Общая длина стен, изображенных на плане дома, должна быть равна 90м. При какой ширине x коридора площадь трех остальных комнат будет наибольшей?

Требуется изготовить конический шатер вместительности V, чтобы на его изготовление пошло наименьшее количество материала. Найти отношение высоты шатра к радиусу основания.
Турист идет из пункта А, находящегося на шоссейной дороге, в пункт В, расположенный в 8 км от шоссе. Расстояние от А до В по прямой составляет 17 км. В каком месте туристу следует свернуть с шоссе, чтобы в кратчайшее время прийти в пункт В, если его скорость передвижения по шоссе 5 км/ч, а по бездорожью 3 км/ч?
Из прямоугольного листа жести размером
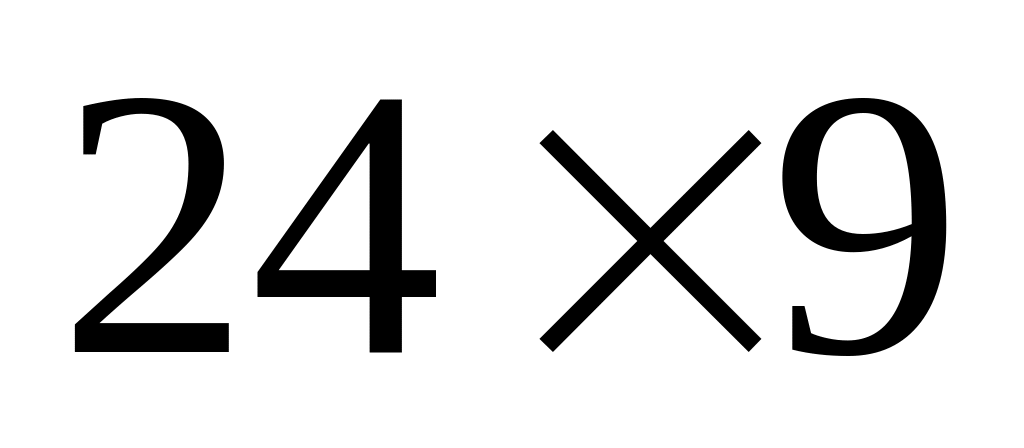 см
требуется изготовить открытую коробку,
вырезая по углам листа равные квадраты
и загибая оставшиеся боковые полосы
под прямым углом. Какова должна быть
сторона вырезаемых квадратов, чтобы
вместимость коробки была наименьшей?
см
требуется изготовить открытую коробку,
вырезая по углам листа равные квадраты
и загибая оставшиеся боковые полосы
под прямым углом. Какова должна быть
сторона вырезаемых квадратов, чтобы
вместимость коробки была наименьшей?Огород прямоугольной формы огорожен изгородью, длина которой 72м. Каковы должны быть размеры огорода, чтобы его площадь была максимальной?
Требуется изготовить полотняный шатер, имеющего форму прямого кругового конуса заданной вместимости
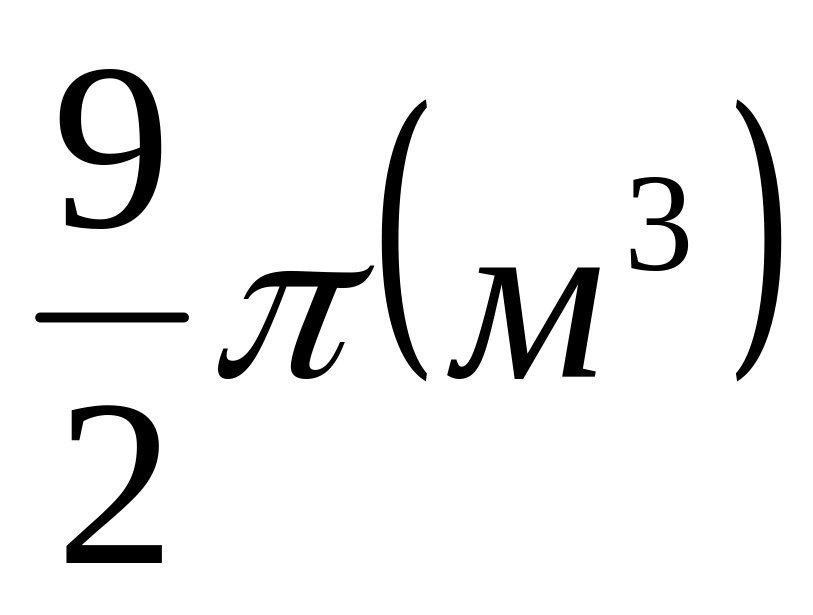 .
Каковы должны быть размеры конуса (
высота и радиус основания ), чтобы на
шатер ушло наименьшее количество
полотна?
.
Каковы должны быть размеры конуса (
высота и радиус основания ), чтобы на
шатер ушло наименьшее количество
полотна?Открытый чан имеет форму цилиндра объема
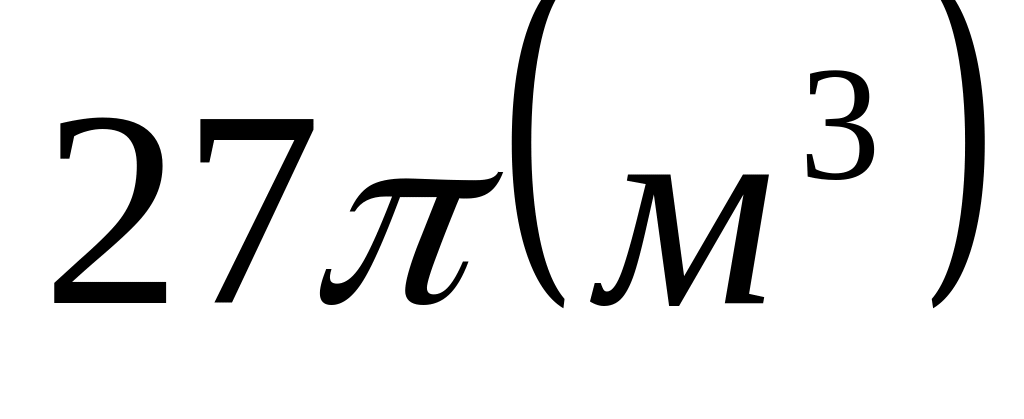 .Каковы
должны быть радиус основания и высота
чана, чтобы на его изготовление ушло
наименьшее количество материала.
.Каковы
должны быть радиус основания и высота
чана, чтобы на его изготовление ушло
наименьшее количество материала.Требуется огородить забором прямоугольный участок земли площадью 294 м2 и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора будет наименьшей?
Корабль К стоит в 9 км от ближайшей точки В прямолинейного берега. С корабля нужно послать курьера в лагерь L , находящийся на берегу и расположенный в 15 км (считая по берегу) от точки В. В каком пункте Р берега курьер должен пристать, чтобы попасть в лагерь в кратчайшее время, если он идет пешком со скоростью 5 км/ч, а на веслах-4 км/ч ?
Какое отношение должно быть между высотой и радиусом закрытой металлической банки, чтобы расход металла не её изготовление был наименьшим?
Какое соотношение должно быть между высотой и радиусом цилиндрической банки без крышки емкостью в 1 л, чтобы на её изготовление пошло наименьше количество материала?
Населенный пункт А расположен на расстоянии 3км от автомагистрали и 5км от города В, через который проходит эта магистраль. Под каким углом к автомагистрали нужно построить подъездную дорогу, чтобы затраты времени на перевозку грузов из А в В были наименьшими, если допустимая скорость движения автомобилей по магистрали –90 км/ч, а по подъездной дороге –45 км/ч?
В прямоугольный треугольник с катетами 2см и 4см, впишите прямоугольник наибольшей площади со сторонами, параллельными катетам треугольника.
Найти высоту и радиус основания цилиндра наибольшего объема, который может быть вписан в конус с радиусом основания 4 см и высотой 10 см.
Какой должна быть высота конуса, вписанного в шар радиуса 20 см, чтобы его объем был наибольшим?
Тело представляет собой прямой круговой цилиндр, завершенный сверху полушаром. При каких линейных размерах (радиус R и высота H) это тело будет иметь полную наименьшую поверхность, если объем его
 ?
?Требуется изготовить открытый сверху цилиндрический сосуд максимальной вместимости. Каковы должны быть размеры сосуда (радиуса R и высота H), если на его изготовление имеется 12π (
 материала
?
материала
?Резервуар, открытый сверху, имеет форму прямоугольного параллелепипеда с квадратным основанием. Каковы должны быть размеры резервуара, чтобы на его лужение пошло наименьшее количество материала, если он должен вмещать 108 л воды?
Решение типовых примеров.
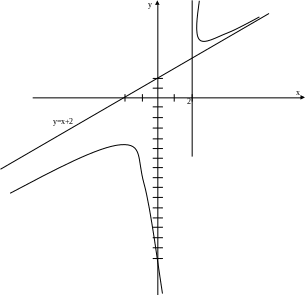
Исследовать функцию и построить её график
![]()
Область определения функции
Функция определена при любом значении аргумента x за исключением x=2. Следовательно, область определения данной функции состоит из двух интервалов:
D(y)=(-∞;2)![]() (2;+∞).
(2;+∞).
Непрерывность функции. Точки разрыва.
При
x=2 функция
терпит разрыв, т.к. y(2)
не
существует. При этом
![]() ,
,
![]()
Четность функции
Т.к область определения не симметрична относительно точки x=0, то функция является ни четной, ни нечетной.
Интервалы возрастания и убывания функции. Точки экстремума.
Определим критические точки первого рода, для чего найдем первую производную:
Решим
уравнение
![]() .
.
![]() ,
отсюда
,
отсюда
![]() .
.
Итак,
мы получили две критические точки:
![]() .
.
Дальнейшее исследование удобно расположить в схему:

Итак, при переходе через точку x=-4 производная меняет свой знак с плюса на минус, следовательно, x=-4 – точка максимума. А при переходе через точку x=8 производная меняет свой знак с минуса на плюс, следовательно, точка x=8 есть точка минимума.
![]()
![]()
При
![]()
![]() функция возрастает, т.к. производная
на этих интервалах неотрицательна.
функция возрастает, т.к. производная
на этих интервалах неотрицательна.
При
![]() функция
убывает, т.к. производная на этом
интервале отрицательна.
функция
убывает, т.к. производная на этом
интервале отрицательна.
Выпуклость и вогнутость графика функции. Точки перегиба.
Найдём вторую производную функции
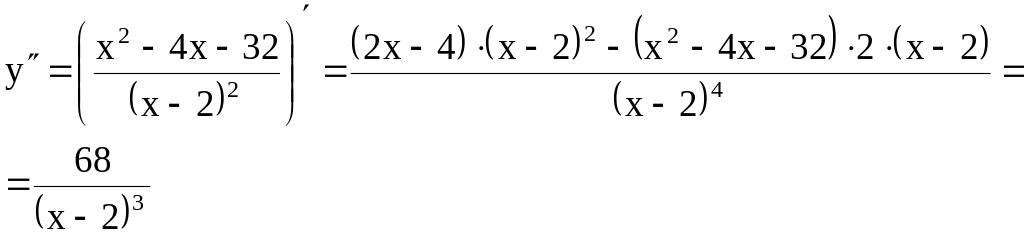
Т.к
вторая производная нигде не обращается
в ноль, то точек перегиба нет. При x<2
вторая
производная отрицательна, следовательно,
при
![]() график функции выпуклый, а при x>2
вторая
призводная больше нуля, следовательно
(2;+∞)
есть
интервал вогнутости графика функции.
график функции выпуклый, а при x>2
вторая
призводная больше нуля, следовательно
(2;+∞)
есть
интервал вогнутости графика функции.
Асимптоты графика функции.
x=2-вертикальная
асимптота. Наклонные асимптоты ищем в
виде
![]() ,
где
,
где
![]() ,
а
,
а
![]() .
Таким образом
.
Таким образом
![]() ,
,
![]() .
Итак
.
Итак
![]() -наклонная
асимптота графика функции.
-наклонная
асимптота графика функции.
Пересечение графика функции с координатными осями. Найдём точки пересечения графика функции с осью (ox), уравнение которой y=0. Из уравнения
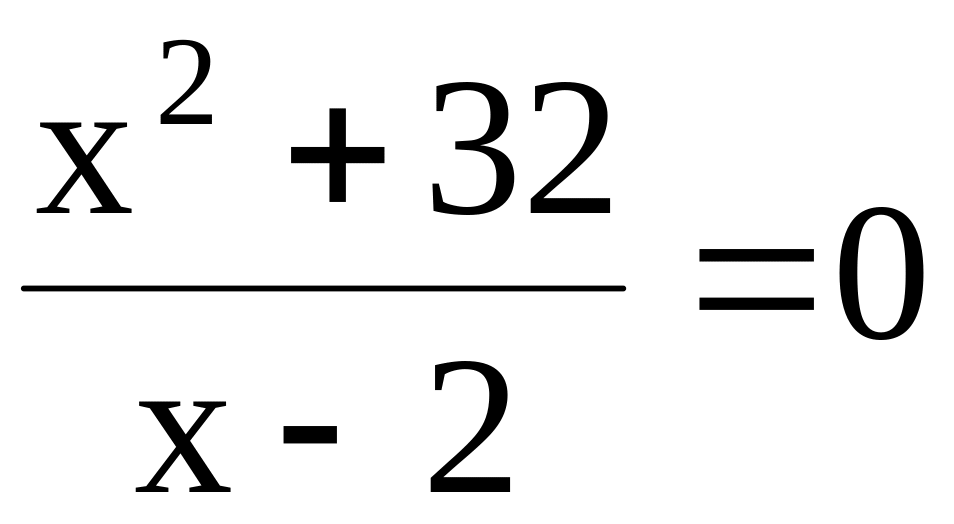 получаем, что таких точек нет.
получаем, что таких точек нет.
Найдем
точки пересечения графика функции с
осью (oy),
уравнение которой x=0.
Найдем y(0)=![]() .
Таким
образом, (0;-16) есть точка пересечения
графика функции с осью (oy).
.
Таким
образом, (0;-16) есть точка пересечения
графика функции с осью (oy).
Поведение функции на бесконечности
![]() ,
,
![]() .
.