55. Линейные и угловые перемещения при изгибе

(рис.126). Перемещение по центра тяжести сечения перпендикулярно к оси балки наз-ся прогибом балки в этом сечении или прогибом. (рис.127). Угол на котором каждое сечение поворачивается по отн-ию к своему первоначальному положению наз-ся углом поворота сечения. - уравнение изогнутой балки. , . Дифференциальное ур-ие изогнутой оси: , , 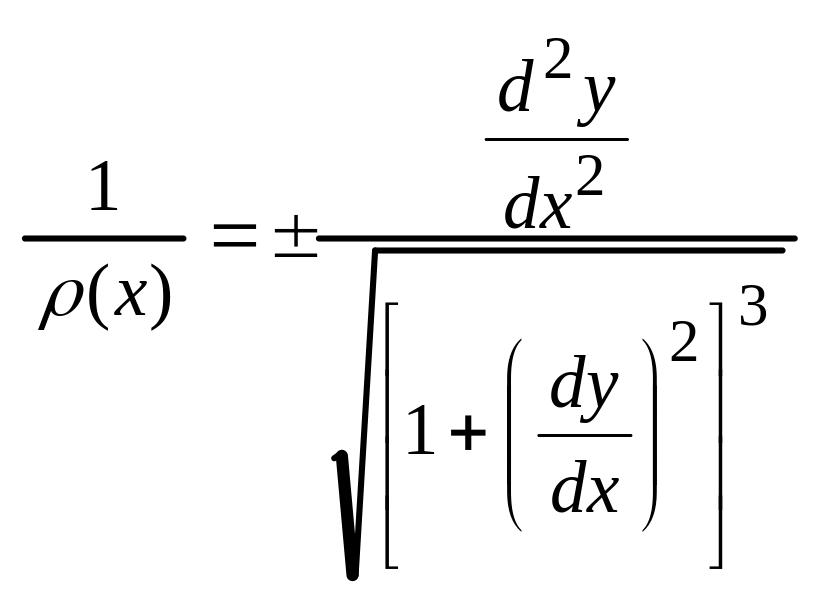, . Проинтегрируем ур-ие: , , Угол поворота сечения: , - ур-ие прогиба

56. Теории прочности

(рис.128). .1) Теория наибольших нормальных напряжений. За критерии прочности прин-ся наибольшее нормальное напр-ие. Предел состояния материала при сложном напряженном состоянии наступает когда наибольшее нормальное напр-ие достигает зн-ия предел напр-ия при одноосном напряженном состоянии. , предел прочности при растяжении. , к – коэффициент запаса. 2) теория наибольших линейных деформаций. В кач-ве критерия прочности прин-ся наиб. линейная деформация. 3) теория наиб.касательных напряжений. Прочность материала при сложном напряженном состоянии считается обеспеченной если наибольшая касательное не превосходит допускаемое касательное установленного для одноосного напряженного состояния. , . При одноосном , . Расчетное зн-ие , расчетное (эквивалентное) напр-ие – напр-ие которое следует создать в растянутом или сжатом образце, чтобы его площадь была одинаковой с прочностью образца нах-ся в условиях сложного напряженного состояния. Недостаток: не учитывается . 4) условие прочности по теореме получившей название теореме потенциальной энергией формы изм-ия записывается так: , , , ,

57. Основные понятия сложного сопротивления

В случае, если в поперечном сечении стержня действуют несколько силовых факторов наз-ся сложным сопр-ем.

58. Совместное действие изгиба и кручения (расчет вала)

Крутящий момент: (Н м), (рис.129). По первой теории: , . По 4 теории: , . Напряжение изгиба: , W – момент сопротивления сечения вала. Касательное кручение: , , расчетный моент (зависит от принятой теории прочности). 1) ; 2) ; 3) ; 4)