3.3. Порядок виконання роботи, обробка результатів вимірів

З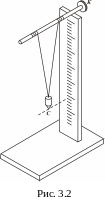 а допомогою барабана К опустити маятник так, щоб його вістря С збігалося з нижнім діленням дзеркальної шкали (не допускаючи паралакса при відліку); відлік за шкалою проводити у тому випадку, коли око бачить вістря маятника, співпадаюче з його дзеркальним зображенням (Рис. 3.2).

Відхилити маятник від положення рівноваги на 5-6° і надати йому можливість вільно коливатися.

Включивши секундомір, коли маятник проходить положення рівноваги, відлічити проміжок часу для 50 повних коливань. Виміри повторити три рази і знайти середній час для 50 коливань при довжині маятника . Обчислити абсолютні погрішності окремих вимірів і середню абсолютну погрішність .

Розділивши на = 50, знайти середній час одного коливання маятника при довжині . Середня погрішність виміру періоду, очевидно .

То ж виконати при іншій довжині маятника , змінивши її на 12-15 см. В цьому випадку період буде , а .

Результати вимірів і обчислень записати в таблиці. 3.1.

Користуючись формулою (3.2), обчислити . Обчислити погрішність :

.

Похибки довжини і ( ) дорівнюють половині ціни ділення шкали, тобто 0,5 мм = 5*10^-4 м.

Результати вимірів записати у вигляді: м/с².

Таблиця 3.1

, м		, с	, с	, с	, с	, с	, с
	50
, м		, с	, с	, с	, с	, с	, с
	50

3.4. Питання для самоперевірки

1) Що називається математичним маятником?

2) Запишіть формулу, що виражає період коливання математичного маятника.

3) Запишіть робочу формулу, якою ви користувалися при обчисленні прискорення сили тяжіння Землі .

4) Чому не визначається безпосередньо з формули для періоду коливань математичного маятника?

5) Як залежить від геометричної широти і висоти від поверхні Землі?

6) Як визначаються абсолютні похибки: і , і .

7) Записати рівняння гармонійного коливання і дати визначення величин, що входять в нього.

8) Вказати сили, що діють на маятник, що знаходиться в положенні рівноваги, а також, коли він відхилиться від положення рівноваги.

3.5. Оформлення звіту

Звіт повинен містити наступні дані: мета роботи; рисунок установки; таблицю результатів вимірів; розрахунок і похибки вимірів; висновки по роботі.

Література: [1], с. 231 – 232; [2], с. 17; [4], с. 181 – 185, 233 – 235.

Лабораторна робота М-4

ВИЗНАЧЕННЯ КОЕФІЦІЄНТА В'ЯЗКОСТІ

МЕТОДОМ СТОКСУ

4.1. Мета роботи

Визначення коефіцієнта внутрішнього тертя рідини.

4.2. Загальні положення

У рухомій рідині між окремими її шарами, що переміщаються з різною швидкістю, діє сила внутрішнього тертя (сила в'язкості). Ця сила, згідно теорії Ньютона, пропорційна коефіцієнту в'язкості , градієнту швидкості (зміна швидкості на одиниці довжини в напрямі, перпендикулярному напряму руху рідині) і площі торкання шарів рідини

.

(4.1)

Сила внутрішнього тертя діє по дотичній до границі між двома сусідніми шарами. Вона прискорює рух шарів, лежачих по один бік від границі, і уповільнює рух шарів, лежачих по інший бік від неї.

Коефіцієнтом в'язкості називають величину, рівну силі тертя, що виникає в рідині між двома шарами одиничної площі, якщо градієнт швидкості між ними дорівнює одиниці. Розмірність коефіцієнта в'язкості встановлюється з формули (4.1). У одиницях СІ

В'язкість рідини виявляється, наприклад, при русі в ній тіла. При цьому шари рідини, безпосередньо прилеглі до тіла, рухаються разом з ним (мають таку ж швидкість, як і тіло), інші шари рухаються з швидкістю, що все зменшується. Шари ж, досить віддалені, залишаються в спокої. Між шарами рідини при цьому виникають сили внутрішнього тертя, які протидіють руху тіла.

Згідно із законом, встановленим Стоксом, сила опору середовища пропорційна швидкості руху тіла, коефіцієнту в'язкості і лінійним розмірам тіла при заданій формі.

Для кульок, що рухаються у в'язкій рідині, що тягнеться безмежно (тобто без врахування наявності стінок, що обмежують судину з рідиною), сила внутрішнього тертя

(4.2)

де – радіус кульки; – його швидкість.

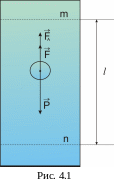
На кульку, що падає у в'язкій рідині, окрім сили в'язкості, направленої вертикально вгору, діють ще дві сили: сила тяжіння Р, направлена вертикально вниз, і виштовхуюча сила F (за законом Архімеда), направлена вгору. Під дією цих трьох сил кулька рухається прискорено, поки швидкість її невелика (і сила в'язкості пропорційна швидкості). Із збільшенням швидкості падіння зростає сила в'язкості і врівноважує силу . Сила тяжіння (або вага кульки) Р і виштовхуюча сила (або вага рідини в об'ємі кульки) можуть бути виражені через об'єм кульки і щільності кульки і рідини, тобто

,

(4.3)

де – щільність кульки;

– щільність рідини;

– радіус кульки;

– прискорення сили тяжіння.

Коли сила урівноважиться силою , кулька почне рухатися рівномірно з постійною швидкістю . Її рух буде сталим. Для цього випадку можна записати:

.

Вирішивши рівняння відносно коефіцієнта в'язкості, отримаємо:

.

Швидкість рівномірного руху можна визначити, вимірявши час проходження кулькою певного шляху : . Тоді формула (4.3) перепишеться у вигляді:

,

(4.4)

де – діаметр кульки.

Знаючи величини, що знаходяться в правій частині рівності, можна визначити коефіцієнт внутрішнього тертя рідини, сильно залежний від температури і такий, що зменшується з її зростанням.
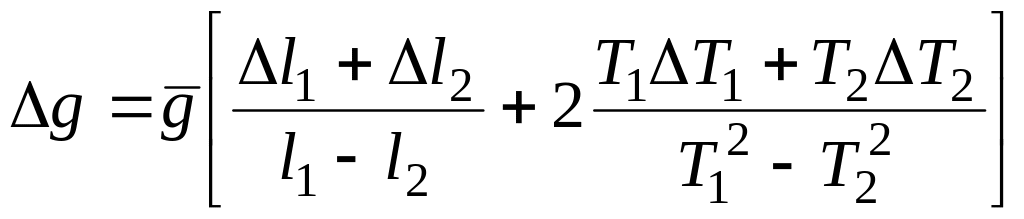