2.5.2. Визначення моменту інерції приладу з додатковими вантажами на стрижнях
Закріпити симетрично вантажі на кінцях стрижнів так, щоб маятник знаходився в положенні байдужої рівноваги, якої добиваються, злегка переміщаючи вантажі на стрижнях.
Повторити
виміри, вказані в п.2.5.1. Знайти
.
Результати вимірів занести до таблиці.
2.1.
По
середніх значеннях величин
,
,
і формулам (2.5) і (2.7) визначити
і
,
і по формулі (2.1) обчислити момент інерції
приладу з додатковими вантажами
.
2.5.3. Перевірка співвідношення (2.4)
Пересунути
вантажі з кінців на середини стрижнів
і виконати виміри, вказані в п.2.5.1. Знайти
час падіння
,
результати занести в таблиці. 2.1.
Провести
розрахунки
і
по формулах (2.5) і (2.7). Обчислити за
формулою (2.1)
.
Перевірити
справедливість співвідношення
2.5.4. Перевірка співвідношення (2.3)
Положення додаткових вантажів на стрижнях не міняти.
Висоту гирі залишити колишньою.
Нитку намотати на шків меншого радіусу і повторити виміри, вказані в п.2.5.1. Визначити . Результати занести в таблиці. 2.1.
Виміряти штангенциркулем діаметр малого шківа в декількох місцях і визначити середнє значення радіусу .
По
формулах (2.5) і (2.7) обчислити
і
,
і перевірити співвідношення
,
узявши значення
і
,
обчислені при виконанні п. 2.5.3.
2.6. Оформлення звіту
Звіт повинен містити наступні дані: мета роботи; рисунок установки (див. Рис. 2.1); таблицю 2.1 з даними, отриманими в результаті виконання пп. 2.5.1, – 2.5.4; розрахунок кутових прискорень, моментів сили і моментів інерції за даними таблиці. 2.1 і формулам (2.5), (2.7) і (2.1); перевірка співвідношень (2.3) і (2.4); висновки по роботі.
Література: 1], с. 34 – 40; [2], с. 48 – 51; [4], с. 101 – 109.
Лабораторна робота М-3
ВИЗНАЧЕННЯ ПРИСКОРЕННЯ СИЛИ ТЯЖІННЯ ЗА ДОПОМОГОЮ МАТЕМАТИЧНОГО МАЯТНИКА
3.1 Мета роботи
Визначення прискорення сили тяжіння за допомогою математичного маятника.
3.2. Загальні положення
Тіло, що здійснює коливання під дією сили тяжіння, називають маятником. Маятник вважають математичним, якщо його можна представити як матеріальну точку, підвішену на довгій нерозтяжній нитці, вагою якої можна нехтувати в порівнянні з вагою самого маятника.
У
прямовисному положенні сила тяжіння P
маятника врівноважується натягненням
нитки, маятник знаходитиметься у спокої
(положенні рівноваги). Якщо відхилити
маятник від положення рівноваги, то він
здійснюватиме коливання. На рис. 3.1
видно, що при відхиленні маятника на
деякий кут
силу тяжіння (вагу) можна розкласти на
дві складові
і
.
Складова
,
паралельна нитці, врівноважується її
натягненням, а складова
,
перпендикулярна до нитки, не врівноважується
іншими силами і приводить в рух маятник.
Маятник здійснюватиме коливальні рухи
біля положення рівноваги.
Д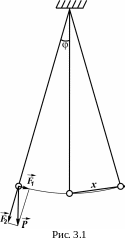
овжину
дуги, на яку відхиляється маятник від
положення рівноваги, називають зсувом.
При невеликих відхиленнях (
5°)
або
і сила
,
аналогічна пружній силі:
,
де
– зсув;
– коефіцієнт
пропорційності.
Знак мінус узятий тому, що складова сили тяжіння Р, надає маятнику прискорення в напрямі, зворотному відхиленню. Як доведено теорією, під дією сили маятник здійснюватиме гармонійний коливальний рух з періодом
|
(3.1) |
,де – довжина математичного маятника (відстань від точки підвісу до центру тяжіння маятника);
– прискорення сили тяжіння.
Таким чином, період коливання математичного маятника залежить від довжини маятника і прискорення сили тяжіння э даному місці земної кулі.
Якщо відомі час повного коливання (період ) і довжина , то з рівняння (3.1) можна знайти прискорення сили тяжіння. Оскільки в умовах досліду довжину маятника визначити важко (трудність полягає у визначенні центру тяжіння), то вимірюють період при двох різних довжинах:
|
(перший вимір)
|
|
(другий вимір)
|
,
,З цих двох рівнянь знаходимо:
|
(3.2) |
,
Як
випливає з рівняння (3.2), для визначення
потрібно виміряти лише значення періодів
і
при двох різних довжинах маятника
і
і визначити різницю цих довжин. При
такому способі відпадає необхідність
знаходити центр тяжіння маятника. Отже,
визначення
буде точнішим.