МІНІСТЕРСТВО ОСВІТИ і НАУКИ, молоді та спорту УКРАЇНИ
УКРАЇНСЬКА ІНЖЕНЕРНО-ПЕДАГОГІЧНА АКАДЕМІЯ
Кафедра фізики, теоретичної і загальної електротехніки
Фізика
«МЕХАНІКА. МОЛЕКУЛЯРНА ФІЗИКА
І ТЕРМОДИНАМІКА»
Методичні вказівки до лабораторних робіт М1 – М5
Для студентів денної та заочної форм навчання всіх спеціальностей
Затверджено
Науково-методичною
радою Української
інженерно- педагогічної
академії протокол
№ 2 від 11.10.11
Харків 2011
УДК 531:534 (076.5)
«ФІЗИКА: «МЕХАНІКА. МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА», методичні вказівки до лабораторних робіт М1 – М5 для студентів денної та заочної форм навчання всіх спеціальностей /Укл. Д.В. Руденко, О.В. Шурінова, І.В. Компанієць – Х.: УІПА, 2011. - 28 с.
В методичних вказівках розглянуті питання розділів «МЕХАНІКА», «МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА» першої частини курсу загальної фізики. Матеріал методичних вказівок відповідає типовим програмам з фізики для студентів інженерних та інженерно-педагогічних спеціальностей.
Рецензент: к.фіз.-мат. н., доц. Хохлов В.І.
|
© Руденко Д. В., 2011 © Шурінова О. В., 2011 © Компанієць І.В., 2011 © УІПА, 2011 |
ЗМІСТ
Лабораторна робота М-1.
ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ МЕТОДОМ
ТРІФІЛЯРНОГО ПІДВІСУ...............................................................................4
Лабораторна робота М-2
ВИВЧЕННЯ ЗАКОНІВ ОБЕРТАЛЬНОГО РУХУ
НА МАЯТНИКУ ОБЕРБЕКА…………………………………......................8
Лабораторна робота М-3
ВИЗНАЧЕННЯ ПРИСКОРЕННЯ СИЛИ ТЯЖІННЯ ЗА
ДОПОМОГОЮ МАТЕМАТИЧНОГО МАЯТНИКА………………..........12
Лабораторна робота М-4
ВИЗНАЧЕННЯ КОЕФІЦІЄНТА В‘ЯЗКОСТІ
МЕТОДОМ СТОКСУ………………………………………….....................15
Лабораторна робота М-5
ВИЗНАЧЕННЯ ВІДНОШЕННЯ ПИТОМИХ
ТЕПЛОЄМНОСТЕЙ ГАЗІВ…………………………...................................21
Лабораторна робота М-1
ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ МЕТОДОМ
ТРІФІЛЯРНОГО ПІДВІСУ
1.1. Мета роботи
Визначення моменту інерції тіла за допомогою тріфілярного підвісу.
1.2. Загальні положення
Тріфілярний
підвіс складається з платформи у формі
диска радіусу
,
підвішеного на трьох симетрично
розташованих нитках, укріплених в країв
диска (Рис. 1.1).
Н
агорі
нитки також симетрично прикріплені до
диска меншого радіусу
.
Якщо нижній диск обернути на невеликий
кут довкола вертикальної осі, що проходить
через його центр, то всі три нитки
приймають похиле положення, і центр
тяжіння платформи переміщається уздовж
осі обертання. При цьому виникає момент
сил, прагнучий повернути платформу в
положення рівноваги. В результаті
платформа здійснює крутильні коливання.
Період коливань визначається величиною моменту інерції платформи: він зміниться, якщо платформу навантажити яким-небудь тілом. Цим способом і користуються в цій роботі.
Якщо
платформа масою
,
обертаючись в одному напрямі, піднялася
на висоту
,
то приріст потенційної енергії
|
|
,
де
– прискорення сили тяжіння.
Обертаючись в іншому напрямі, платформа прийде в положення рівноваги з кінетичною енергією
|
|
,
де
– момент інерції платформи,
– кутова швидкість платформи у момент
досягнення положення рівноваги.
Нехтуючи роботою сил тертя, на підставі закону збереження механічної енергії маємо:
|
(1.1) |
.Вважаючи, що платформа здійснює гармонійні коливання, можна написати залежність кутового зсуву платформи від часу обертання у вигляді:
|
|
,
де
– кутовий зсув платформи;
– амплітуда зсуву;
– період повного коливання.
Кутова швидкість є першою похідною за часом:
|
|
.
У момент
проходження через положення рівноваги
(
,
,
,
і так далі) абсолютне значення цієї
величини
|
(1.2) |
.На підставі виразів (1.1) і (1.2) маємо:
|
(1.3) |
.
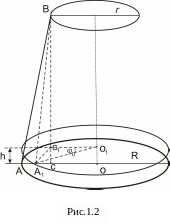
Якщо
– довжина ниток підвісу,
– радіус платформи,
– радіус верхнього диска, то легко
бачити з рис.1.2, що
|
|
.Оскільки
|
|
|
|
,
,отримаємо:
|
|
.
При
малих відхиленнях
синус цього кута можна замінити
аргументом, а величину знаменника
покласти рівною
.
Враховуючи це, маємо:
|
|
.Тоді на підставі (1.3)
|
|
,звідки
|
(1.4) |
.По формулі (1.4) можуть бути визначені момент інерції самої платформи і тіла, покладеного на неї.
Обертальний імпульс, необхідний для початку крутильних коливань, надається платформі шляхом повороту важеля спеціального пускового пристрою, пов'язаного з верхнім диском. Цим майже повністю усуваються інші, некрутильні коливання, наявність яких утрудняє виміри.
