СОДЕРЖАНИЕ
Введение…………………………………………………………………………………….3
1. Задание по выполнению лабораторной работы………………………………………4 2. Порядок выполнения работы…………………………………………..………………5 3. Контрольные вопросы………………………………………………………….………9 Заключение…………………………………………………………………………………11 Библиография……………………………………………………………………….……...12
ВВЕДЕНИЕ
Регрессионный анализ предназначен для установления функциональной связи между одной зависимой переменной и одной или несколькими независимыми переменными.
Задачи математического моделирования экономических показателей часто возникают в экономике и задачах управления. Получаемые модели используют для прогнозирования состояния процессов, более глубокого их изучения и управления ими.
Целью выполнения лабораторной работы является применение теоретических знаний по теме «Одномерный регрессионный анализ» при решении экономических задач с помощью системы GRETL. Методические указания предназначены для студентов экономических специальностей.
Задание по выполнению лабораторной работы
Задание 1
Компания «Лагуна», которая обеспечивает стеклянными бутылками множество изготовителей безалкогольных напитков, обладает следующей информацией, относящейся к числу ящиков при одной отгрузке и соответствующим транспортным затратам.
Задание 2
Компания «Фаворит» продает компьютерные программы. Ее отдел маркетинга получил данные (количество программ, цены программ, средний доход потребителей, приобретающих такой товар) из филиалов компании, расположенных по территории области (см. Таблицу 5.2).
Проведите анализ спроса на продукцию фирмы. Подберите наилучшую модель, описывающую зависимость спроса от цены или дохода (линейную, квадратичную, кубическую). Представьте экономическое обоснование результатов регрессионного анализа.
Задание 3
Менеджер торгового предприятия, занимающегося реализацией продуктов питания, имеет следующие данные о ежеквартальной оборачиваемости оборотных средств и уровне рентабельности. Проанализируйте эти данные и составьте регрессионную модель зависимости рентабельности от оборачиваемости оборотных средств.
Задание 4
По статистическим данным, описывающим зависимость уровня рентабельности на предприятии от удельного веса продовольственных товаров в товарообороте построить уравнение регрессии.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1
Модель 1: МНК, использованы наблюдения 1-10
Зависимая переменная: y
|
Коэффициент |
Ст. ошибка |
t-статистика |
P-значение |
|
const |
101,775 |
35,4884 |
2,8678 |
0,02090 |
** |
x |
2,08615 |
0,0559348 |
37,2962 |
<0,00001 |
*** |
Среднее зав. перемен |
1303,400 |
|
Ст. откл. зав. перемен |
586,6466 |
Сумма кв. остатков |
17711,94 |
|
Ст. ошибка модели |
47,05308 |
R-квадрат |
0,994282 |
|
Испр. R-квадрат |
0,993567 |
F(1, 8) |
1391,006 |
|
Р-значение (F) |
2,93e-10 |
Лог. правдоподобие |
-51,58643 |
|
Крит. Акаике |
107,1729 |
Крит. Шварца |
107,7780 |
|
Крит. Хеннана-Куинна |
106,5090 |

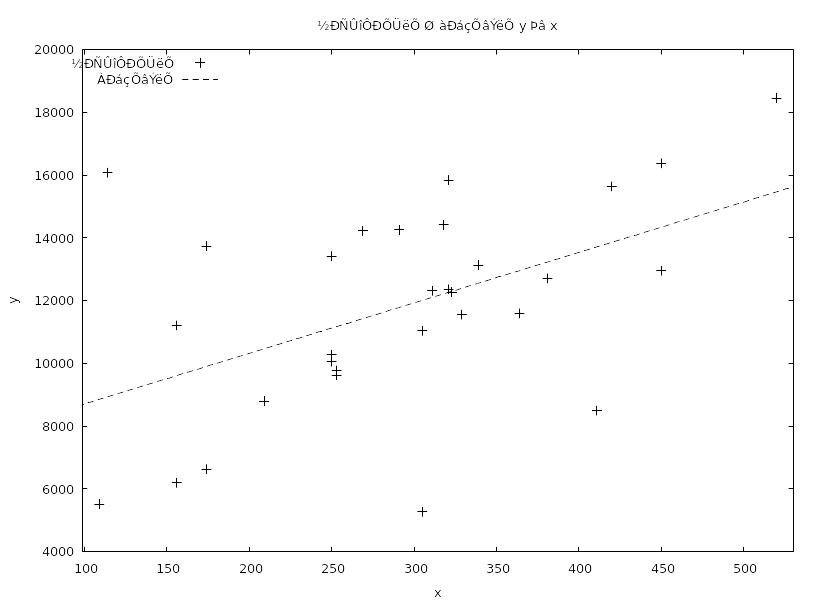
Задание 2
Модель 1: МНК, использованы наблюдения 1-30
Зависимая переменная: y
|
Коэффициент |
Ст. ошибка |
t-статистика |
P-значение |
|
const |
7104,04 |
1663,89 |
4,2695 |
0,00020 |
*** |
x |
16,0864 |
5,38309 |
2,9883 |
0,00578 |
*** |
Среднее зав. перемен |
11809,83 |
|
Ст. откл. зав. перемен |
3321,213 |
Сумма кв. остатков |
2,43e+08 |
|
Ст. ошибка модели |
2943,108 |
R-квадрат |
0,241809 |
|
Испр. R-квадрат |
0,214731 |
F(1, 28) |
8,929997 |
|
Р-значение (F) |
0,005782 |
Лог. правдоподобие |
-281,1499 |
|
Крит. Акаике |
566,2998 |
Крит. Шварца |
569,1022 |
|
Крит. Хеннана-Куинна |
567,1963 |