Ковариация и корреляция

Выборочной ковариацией двух переменных х, у называется средняя величина произведения отклонений этих переменных от своих средних, т. е.

или

где , — выборочные средние переменных х, у.

Ковариацию можно вычислить с помощью функции Excel КОВАР(массив1; массив2), где Массив 1 и 2  это значения x и y.

Выборочная ковариация является мерой взаимосвязи между двумя переменными.

Пусть данные наблюдений переменных х, у представлены в виде точечного графика – диаграммы рассеяния наблюдений

Точка на диаграмме является центром рассеяния переменных х, у.

Вертикальная и горизонтальная прямые, проведенные через точку , разделяют диаграмму рассеяния на четыре области.

Наблюдения в областях I, III дают положительный вклад в ковариацию, а в областях II, IV — отрицательный.

Если положительные вклады преобладают над отрицательными, то ковариация будет положительной, в противном случае она будет отрицательной. Положительной ковариации отвечает положительная связь, а отрицательной — отрицательная.

При положительной (прямой) связи с увеличением одной переменной другая переменная в среднем также увеличивается, и наоборот при отрицательной (обратной) связи.

Заметим, что

Свойства ковариации:

1. ;

2. , где а – константа;

3. , где а – константа;

4. 

Пусть выборка извлечена из нормальной генеральной совокупности и отражает ее свойства.

Если случайные величины X, У независимы, то ковариация равна нулю и выборочные точки на диаграмме рассеяния наблюдений можно заключить в окружность с центром в точке .

Если X, У зависимы, то ковариация отлична от нуля и выборочные точки можно заключить в эллипс с центром в точке , при этом положение большей полуоси эллипса будет указывать направление связи (положительная или отрицательная).

Более точной мерой зависимости между величинами является коэффициент корреляции.

Выборочный коэффициент корреляции определяется выражением

,

он является безразмерной величиной и показывает степень линейной связи двух переменных.

Коэффициент корреляции можно вычислить с помощью функции Excel КОРРЕЛ(массив1; массив2), где Массив 1 и 2  это значения x и y.

Свойства коэффициента корреляции:

1. ;

2. ;

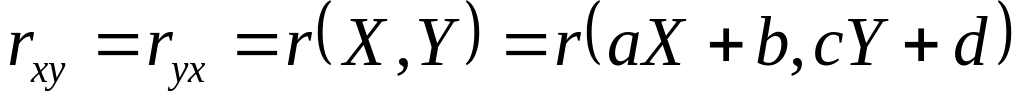3. если 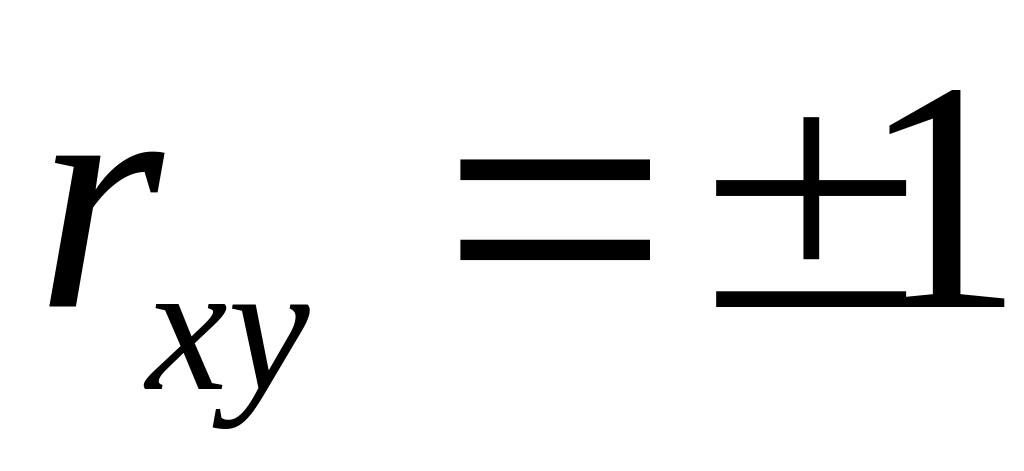, то X и Y точно связаны линейной функциональной зависимостью;

4. если , то между X и Y нет линейной корреляционной зависимости, но это не исключает существования другого вида зависимости;

5. если , то имеет место прямая корреляционная зависимость;

6. если , то имеет место обратная корреляционная зависимость.

На рисунках отражен геометрический смысл коэффициента корреляции. На рисунках а и б случайные величины X, У коррелированы (r > 0 или r < 0), на рисунках в и г — некоррелированы (r = 0). Если r = 0, случайные величины могут быть как зависимыми (см. рис. в), так и независимыми(см. рис. г).

Выборочный коэффициент корреляции является случайной величиной.

Проверка гипотезы о корреляции случайных величин. Пусть по данным выборки объема п получен выборочный коэффициент корреляции r  0. Требуется проверить гипотезу о равенстве нулю истинного значения коэффициента корреляции , т.е,

Статистика определяется по формуле

.

Граничная точка определяется с помощью функции пакета Exel: СТЬЮДРАСПОБР(1− p; n−2).

Пример 7.

Вычислить ковариацию и коэффициент корреляции между расходами на питание у и личным доходом х по данным экономики (усл. ед.) некоторой страны за пять лет. Доверительная вероятность .

Решение.

Вычисляем ковариацию с помощью функции Excel КОВАР(массив1; массив2):

Теперь вычислим коэффициент корреляции по формуле

.

Проверяем полученное значение с помощью функции Excel КОРРЕЛ(массив1; массив2).

Оценим значимость выборочного коэффициента корреляции.

Выдвигаем гипотезы:

: , нет линейной взаимосвязи между переменными;

: , есть линейная взаимосвязь между переменными.

Статистика .

Граничная точка определяется с помощью функции пакета Exel: СТЬЮДРАСПОБР(1−p; n−2). Получаем, = СТЬЮДРАСПОБР(0,05; 3) = 3,18.

Получили, что гипотеза отвергается на уровне значимости 5%, то есть имеется линейная зависимость между переменными.