Испытание гипотез на основе выборочной средней

Рассмотрим случай, когда известна генеральная дисперсия , объем выборки равен n, выборочная средняя равна . Тогда граничные точки: (для правосторонней проверки),  (для левосторонней проверки), (для двусторонней проверки). Значение определяется с помощью функции НОРМСТОБР(1 ) пакета Exel. Статистика вычисляется по формуле .

Пример 4.

Автомат, работающий со стандартным отклонением г. фасует чай в пачки со средним весом г. Проведена случайная выборка объемом пачек. Средний вес пачки чая в выборке г. Надо ли отрегулировать автомат? Доверительная вероятность .

Выдвигаем гипотезы:

H₀ : для нормальной совокупности генеральная средняя г;

H₁ : г.

Проведем двустороннюю проверку.

; вычисляем с помощью функции НОРМСТОБР(10,025), получаем . Следовательно, граничные точки .

Вычисляем статистику .

О тметим значения на числовой оси

Отклоняем гипотезу H₀ и принимаем гипотезу H₁ на уровне значимости 5%. Автомат нужно отрегулировать.

Рассмотрим случай, когда неизвестна генеральная дисперсия . Пусть объем выборки равен n, выборочная средняя равна и выборочное стандартное отклонение равно s. Пусть a  предполагаемое значение генеральной средней. Тогда граничные точки: (для правосторонней проверки),  (для левосторонней проверки), (для двусторонней проверки). Значение определяется с помощью функции пакета Exel: СТЬЮДРАСПОБР(2(1−p); n−1) для правосторонней и левосторонней проверки и СТЬЮДРАСПОБР(1−p; n−1) для двусторонней проверки. Статистика вычисляется по формуле .

Пример 5.

Производитель утверждает, что средний вес пачки чая не меньше г. Инспектор отобрал 10 пачек и взвесил. Их вес оказался равным 97, 102, 103, 98, 96, 105, 98, 100, 101, 99 г соответственно. Не противоречит ли это утверждению производителя? Предполагается, что вес пачек распределен нормально. Доверительная вероятность .

Выдвигаем гипотезы:

H₀ : для нормальной совокупности генеральная средняя г;

H₁ : г.

Проведем левостороннюю проверку.

; вычисляем с помощью функции СТЬЮДРАСПОБР(2(0,01); 9), получаем . Следовательно, граничная точка равна −2,821.

Вычислим и s с помощью функции Excel.

Вычисляем статистику .

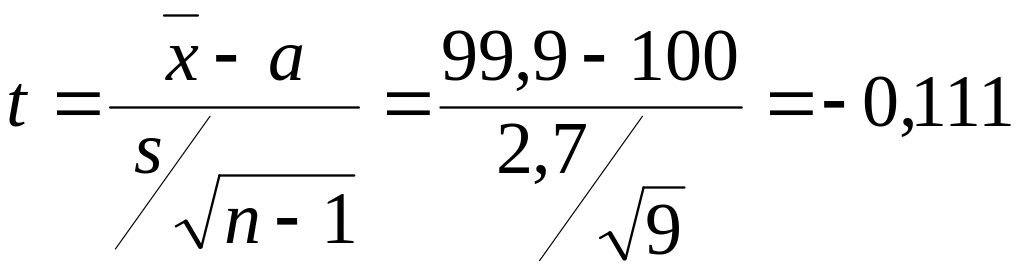О тметим значения на числовой оси

Отклонение H₀, принятие H₁

1%

Принятие H₀

99%

− 2,821

− 0,111

Принимаем гипотезу H₀ на уровне значимости 1%. Выборка инспектора не противоречит утверждению производителя.

Испытание гипотез о двух генеральных дисперсиях

Очень часто про две независимые выборки объема и соответственно нужно узнать, взяты ли они из нормальных генеральных совокупностей с одинаковой дисперсией. Для каждой выборки нужно определить выборочную дисперсию и . Оценка генеральной дисперсии по первой выборке осуществляется по формуле . Оценка генеральной дисперсии по второй выборке осуществляется по формуле . Статистика вычисляется по формуле

F = (большая оценка генеральной дисперсии)/(меньшая оценка генеральной дисперсии)

Обозначим через объем выборки, у которой больше оценка генеральной дисперсии, через обозначим объем другой выборки. Так как дисперсия неотрицательна, то нам понадобится одна граничная точка , которую находят из таблиц F-распределения (распределения Фишера). Можно воспользоваться функцией пакета Excel FРАСПОБР( ; ; ).

Пример 6.

Инвестиция 1 рассчитана на лет, дисперсия ежегодных прибылей . Инвестиция 2 рассчитана на лет, дисперсия ежегодных прибылей . Предполагается, что распределение ежегодных прибылей на инвестиции подчиняется нормальному закону распределения. Равны ли риски инвестиций 1 и 2? Доверительная вероятность p = 95%.

Выдвигаем гипотезы:

H₀ : (риски инвестиций равны);

H₁ : (риски инвестиций не равны).

Оценка генеральной дисперсии по первой выборке .

Оценка генеральной дисперсии по второй выборке .

Статистика F = (большая оценка генеральной дисперсии)/(меньшая оценка генеральной дисперсии) = 33,333/21,818 = 1,528.

Так как 33,333 > 21,818, то , . Проведем двустороннюю проверку.

; вычисляем с помощью функции FРАСПОБР(0,025;9;11), получаем значение 3,588. Следовательно, граничные точки .

О тметим значения на числовой оси

Принимаем гипотезу H₀ на уровне значимости 5%. Риски инвестиций равны.