15

Лабораторная работа № 1 обработка результатов измерений

Введение

Критерий согласия хи-квадрат (Пирсона)

Обработка результатов прямых равноточных измерений

Обработка результатов косвенных измерений

Программа статистической обработки измерений

Литература

Цель работы: научиться обрабатывать экспериментальные данные равноточных измерений.

Приборы и принадлежности:

1. Персональный компьютер.

2. Программа статистической обработки экспериментальных данных.

Введение

Измерение – совокупность операций, выполняемых с помощью технического средства, хранящего единицу величины, позволяющего сопоставить измеряемую величину с ее единицей и получить значение величины. Это значение называют результатом измерений.

Результат измерений должен сопровождаться указанием погрешности, с которой он получен.

Погрешность измерений – отклонение результатов измерений от истинного (действительного) значения измеряемой величины.

Истинное значение физической величины неизвестно и применяется в теоретических исследованиях; действительное значение величины определяется экспериментально из предположения, что результат эксперимента (измерения) наиболее близок к истинному значению величины.

Цель любого измерения – это получение результата измерений с оценкой истинного значения измеряемой величины. Для этого проводится обработка результатов измерений, в большинстве случаев с помощью вероятностно-статистических методов теории вероятностей и математической статистики.

Считается, что однократные измерения допустимы только в порядке исключения, так как они по существу не позволяют судить о достоверности измерительной информации. Если можно принять, что в погрешности результата измерений роль систематической [1] погрешности пренебрежимо мала по сравнению со случайной [2] погрешностью, то при определении необходимого количества измерений следует исходить из возможности проведения статистической обработки результатов измерений. Известно, что при 7 … 8 измерениях оценки их результатов приобретают некоторую устойчивость. Если необходимо получение достоверных результатов измерений, то их число должно быть 25 … 30. Если объект измерений до этого не исследовался и, кроме предварительных, обычно расчетных значений величин, о нем мало что известно, то в этом случае число измерений должно быть увеличено до 50 … 100, а при необходимости нахождения законов распределения оцениваемых величин число измерений целесообразно увеличить на порядок.

Главная цель увеличения числа измерений (если систематическая составляющая погрешности исключена) состоит в уменьшении случайности результата измерений и, следовательно, в наилучшем приближении результата к истинному значению величины. Но увеличивать число измерений с целью найти истинное значение величины бессмысленно.

По результатам измерений чаще всего рассчитывают среднее арифметическое значение и статистическое среднее квадратическое отклонение (СКО) величины. Первое является оценкой математического ожидания величины, а статистическое СКО – оценкой теоретического СКО.

Пусть изучается некоторая случайная величина x. Произведено n независимых измерений с результатами x₁, x₂… x_i … x_n. Для оценки истинного значения измеряемой величины используется среднее арифметическое значение, которое обычно обозначается или (оценка математического ожидания m_x, соответствующего для физической величины ее истинному значению): . (1)

Оценкой дисперсии D_x дискретной величины X является статистическая дисперсия, как статистический второй центральный момент [3]

где – статистическая вероятность значения .

Одним из условий получения надежных оценок является требование к их несмещенности, которое заключается в том, чтобы при замене оценкой истинного значения X_ист не допускалась систематическая погрешность (в сторону увеличения или уменьшения относительно X_ист).

Несмещенной оценкой дисперсии D_x является величина

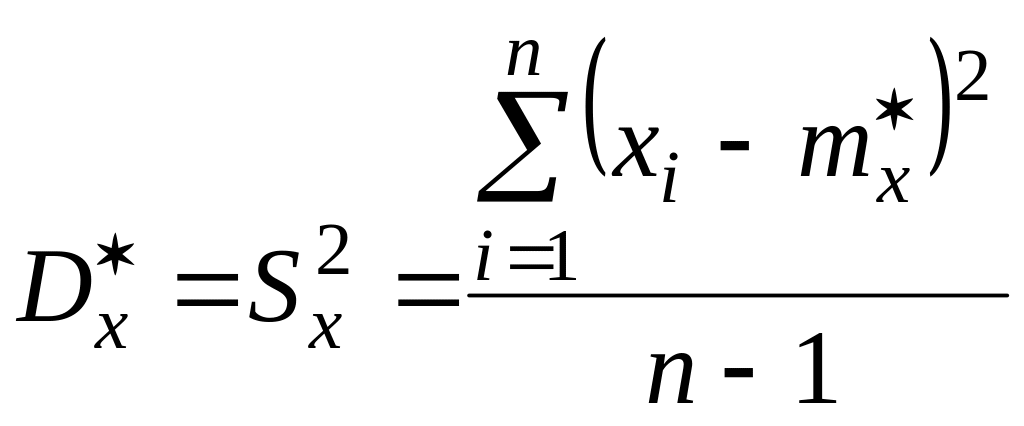_{, (2)}

Статистическое СКО 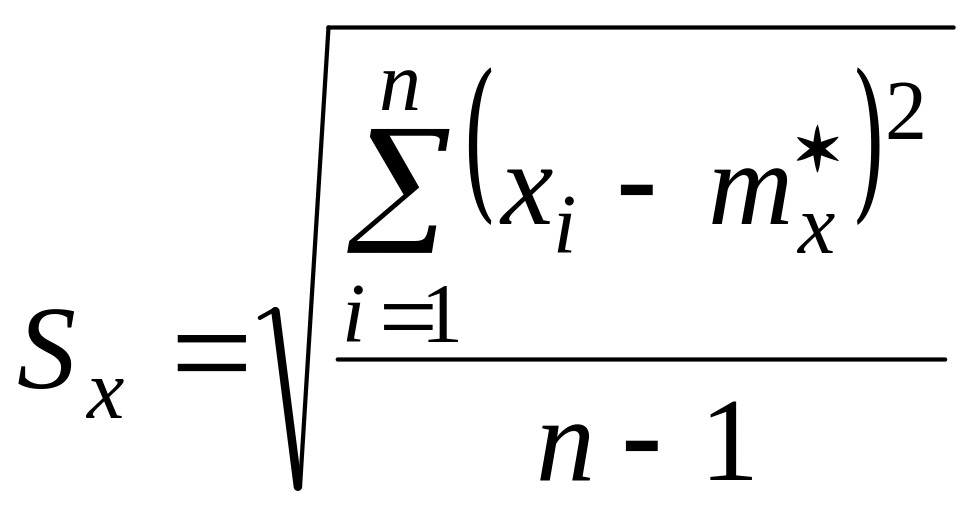_{. (3)}

При обработке результатов измерений приходится встречаться с различными законами распределения измеряемых величин, рассматриваемых как случайные величины: нормальный закон распределения или закон Гаусса, равномерный закон распределения, закон распределения Максвелла, арксинусный закон распределения, треугольный закон распределения, корреляционный закон распределения и т.д.

Нормальный закон распределения величины х представляется плотностью распределения 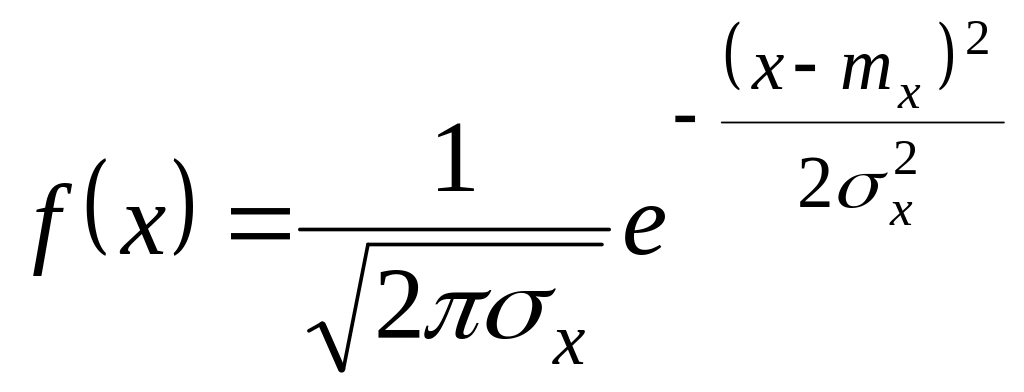_{, (4)}

где – математическое ожидание величины X;

– СКО (теоретическое).

Плотность распределения величины Х является размерной функцией:

_{, [4]}

Кривая плотности распределения величины Х симметрична относительно точки рассеивания, имеющей абсциссу m_x (рис. 1). Параметр σ_х характеризует форму кривой распределения. С увеличением значения σ_х кривая распределения «растягивается» вдоль оси абсцисс.

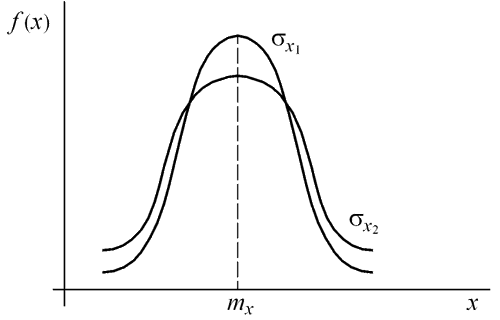
Рис. 1. Нормальный закон распределения

Для некоторого интервала значений от a до b вероятность того, что выполняется

a < X < b

После замены переменной , т.е., :

_{, (5)}

Для вычисления интеграла (5) пользуются таблицами функции Лапласа (приложение А) в виде

_{, (6)}

С помощью функции Лапласа вычисляется интеграл (5)

_{, (7)}

При выполнении точных измерений целесообразно изучить реальную форму закона распределения результатов измерений и учитывать его свойства при обработке этих результатов.

С целью нахождения закона распределения той или иной величины (параметра) производятся сотни и тысячи измерений. После построения эмпирического закона распределения величины необходимо построить соответствующую ему модель теоретического закона распределения, обычно путем сопоставления эмпирической модели известным законам распределения. Эта задача решается с помощью критериев согласия: критерий согласия хи-квадрат (Пирсона), критерий согласия Колмогорова, метод моментов. В зависимости от применяемых критериев согласия закон распределения представляется в виде плоскости распределения, функции распределения или отношений центральных моментов случайной величины.

Отличаясь простотой применения, критерий Колмогорова уступает критерию хи-квадрат по степени доверия к результатам идентификации законов распределения.

Применение метода моментов требует наличия большого количества измерений. Для надежной оценки первого момента (математического ожидания) требуется выборка n ≥ 30, для оценки вторых моментов – n ≥ 100, для оценки третьих моментов – n ≈ 1000. Таким образом, применение метода моментов при обычных, небольших выборках (число измерений не превышает 100) практически ограничено.

Во многих случаях число измерений, превышающее 30 … 40, позволяет использовать их результаты для идентификации закона распределения с помощью критерия хи-квадрат.