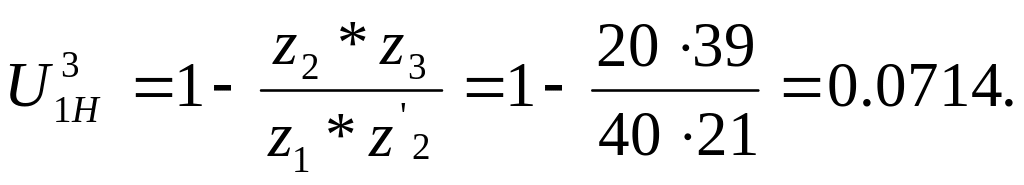Качественные показатели передач

1. Коэффициент перекрытия:

_j=_+_; _=(z₁∙tg _a1+ z₂∙tg _a2-(z₁+ z₂)∙ tg_w)/2∙.

2. Коэффициент удельного скольжения:

₁= ; ₂= ;

U₂₁= z₁/z₂=12/19=0, 63158; U₁₂= z₂/z₁=19/12=1,583.

3. Коэффициент давления в полюсе:

5.2.2. Анализ результатов расчетов на ЭВМ

Для построения картины зубчатого зацепления необходимо выбрать значение зубчатого зацепления, которые приведены в распечатке ЭВМ. Для этого необходимо определить величину x1 – расчетного коэффициента смещения.

Строим диаграмму качественных показателей зацепления(рис.5.2.). Она состоит из нескольких графиков: S_a1=f(x₁), S_a2=f(x₁), ₁=f(x₁), ₂=f(x₁), =f(x₁).

Определение коэффициента смещения будем производить с помощью “блокирующего контура”. Строим зону ограничения по , т.е. проводим линию =1,13. Находим точку пересечения графика =f(x₁) и линии =1,13 и через эту точку проводим зону ограничения по .

Строим зону заострения, т.е. проводим линию k=0,4m=2. Находим точку пересечения графика S_a1=f(x₁) и линии k=0,4m=2 и через эту точку проводим зону заострения.

Строим зону подреза; она строится на расстоянии x_min=0,298.

Выбираем x₁ из контура образованного зоной ограничения по  и зоной подреза, по принципу: x₁ должно быть такое, чтобы расстояние между графиком ₁=f(x₁) и графиком ₂=f(x₁) было наименьшее, т.е. x₁=0,5.

Для найденного коэффициента х₁ выбираем параметры зубчатой передачи.

1. Радиусы делительных окружностей:

r₁=m∙z₁/2; r₂=m∙z₂/2.

2. Радиусы основных окружностей:

r_b1=m∙z₁∙cos/2; r_b2=m∙z₂∙cos/2.

3. Минимальное число зубьев на ведущем колесе, которое можно нарезать без подрезки:

z_min=2∙(h_a*-x)/sin².

4. Минимальный коэффициент смещения:

x_min1,2=h_a*∙(z_min-z)/z_min.

5. Выбор коэффициентов смещения: x1, x2

6. Угол зацепления передачи:

inv_w= inv+(2∙x_∙tg/z₁∙z₂.)

7. Коэффициент воспринимаемого смещения:

y= ( )/m.

8. Коэффициент уравнительного смещения: Δy= x_-y.

9. Радиусы начальных окружностей:

r_w1=2 /( ); r_w2=2 /( ); .

10. Межосевое расстояние:

a_w=a .

11. Радиусы окружностей вершин:

r_a1=m∙(x₁+h_a*- Δy)+r ; r_a2=m∙( x₂+h_a*- Δy)+r .

12. Радиусы окружностей впадин:

r_f1=m∙(x₁-h_a*- c*)+r ; r_f2=m∙(x₂+h_a*- c*)+r .

13. Высота зубьев колес:

h=m∙(2∙h_a*- Δy +c*).

14. Толщина зубьев по нормальной окружности:

S₁=(∙m/2)+2∙x₁∙m∙tg; S₂=(∙m/2)+2∙x₂∙m∙tg.

15. Угол профиля на окружности вершин:

cos_a1=r₁ cos/r_a1; cos_a2= r₂ cos/r_a2;

16. Толщина зубьев по дугам окружностей вершин:

S_a1=m ∙((/2∙z₁)+(2∙x₁∙tg/ z₁)+ inv- inv_a1);

S_a2= m ∙((/2∙z₂)+(2∙x₂∙tg/ z₂)+ inv- inv_a2).

5.3. Синтез планетарного редуктора

Проектирование планетарного редуктора должно быть произведено при следующих условиях:

1. условие соосности.

Как правило, планетарные редукторы собирают из нулевых колёс ( ). Поэтому имеем:

.

Считая, что все колёса имеют один и тот же модуль m, получим:

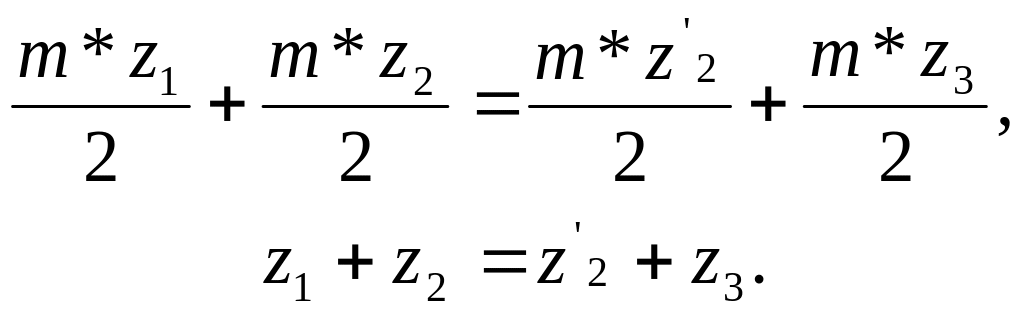
Последнее выражение является условием соосности.

2. условие соседства.

Для увеличения нагрузочной способности планетарных редукторов и уравновешивания водила число сателлитов всегда либо равно, либо больше 2.

.

3. условие сборки.

Сборка планетарного редуктора может быть осуществлена, если

где С – любое целое число.

Определение числа зубьев.

Требуемое передаточное отношение привода :

Требуемое передаточное отношение редуктора:

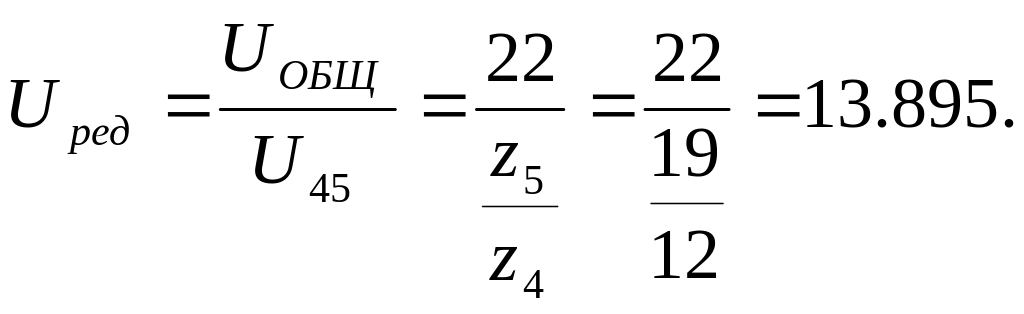
Округлим значение передаточного отношения до 14, при этом погрешность не превысит 2%.

Определим передаточное отношение :

.

По передаточному отношению подсчитываем:

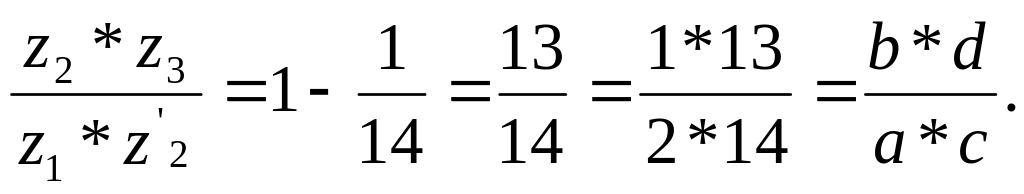
Считая z₁ пропорциональным a; z₂ – b; z₃ – c; z′₂ – d , ищем решение в виде:

z₁ = γ · a (d + c) = γ · 2 (13 + 7) = 40 γ;

z₂ = γ · b (d + c) = γ · 1 (13 + 7) = 20γ;

z₂′= γ · c (a + b) = γ · 7 (1 + 2) = 21γ;

z₃ = γ · d (a + b) = γ · 13(1 + 2) = 39γ.

Берем γ = 1, тогда z₁ = 40; z₂ = 20; z₂′ = 21; z₃ = 39.

Проверяем условие соосности: 40 + 20 = 21 + 39.

60 = 60

Условие соосности выполняется.

Проверим результаты по условию соседства:

.

Оно тоже выполняется: 0.7071 > 0.3666.

Проверяем условие сборки: C = 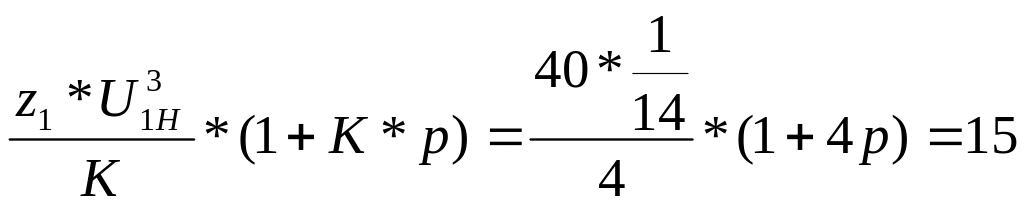при p = 5.

Сборка будет обеспечена с четырьмя сателлитами при φ_Н = 90^о.

Определим расчётное передаточное отношение редуктора:

Относительная погрешность:

Определим радиусы колёс:

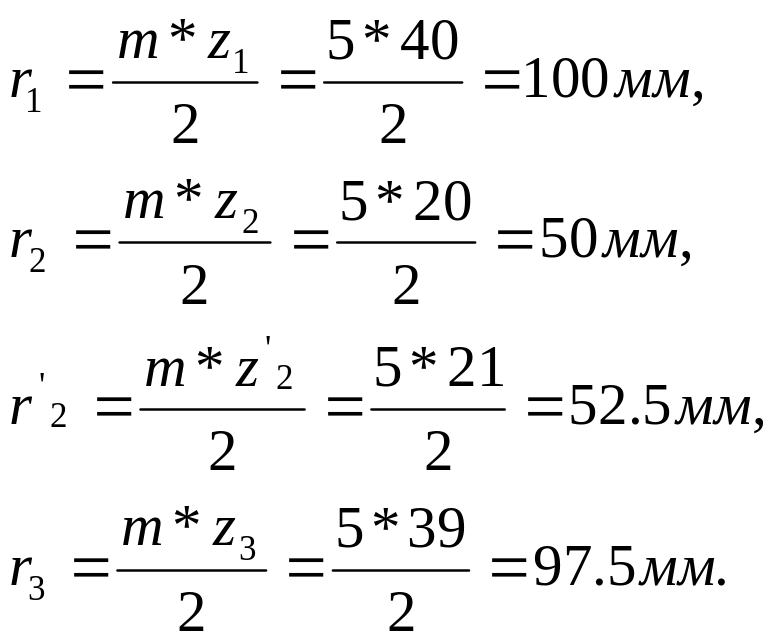
5.4. Определение передаточных отношений зубчатых передач графическим методом.

Выбираем масштабный коэффициент:

Строим картину линейных скоростей. Для этого на вертикальную прямую сносим все характерные точки планетарного редуктора О₁, О₂, А, В.

Определяем скорость точки А: ,

.

и

Следовательно,

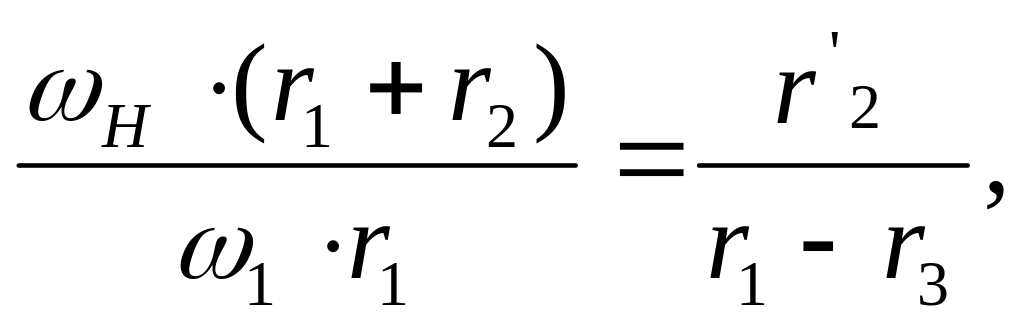
откуда

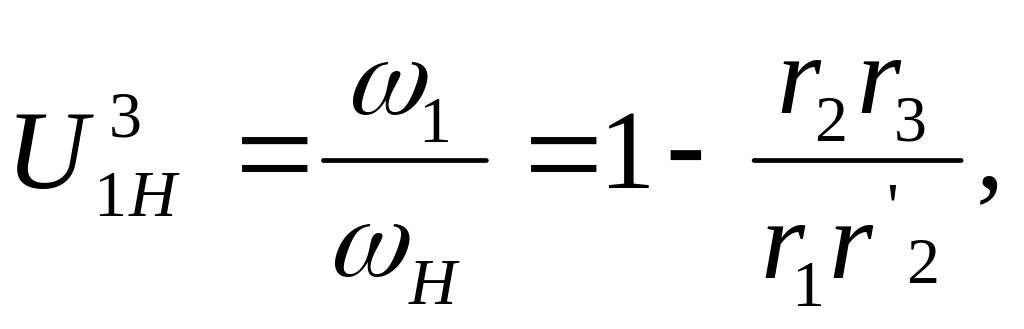
так как Заменяя отношения радиусов отношением чисел зубьев, получаем: