Алгоритм метода Фибоначчи состоит из следующих этапов:

1. Изменяют масштаб исходного интервала, в котором лежит оптимум. В качестве единицы измерения принимают 1=X₀/F_N, или если задана длина l, в котором лежит оптимум, находят его на исходном интервале длиной X₀. Для этого, разделив X₀ на 1, находят ближайшее большее число Фибоначчи F_N, а по нему определяют N – число необходимых расчётов для определения интервала.

2. Расставляют первые две точки и на интервале исследования X₀ на расстоянии F_N-2 от конца b.

3. Вычисляют значение целевой функции в этих точках для сужения интервала исследования. Пусть > , тогда интервал [ , F_N] исключается из рассмотрения.

4. На новом интервале исследования снова расставляют две точки 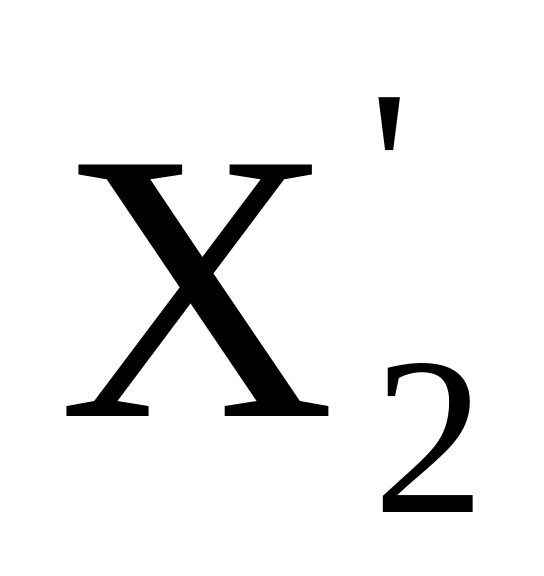и , но в одной из них уже известно значение целевой функции = .

5. Переходят к этапу 3 и т.д., пока не достигают искомого интервала, в котором находится значение переменной, максимизирующее её целевую функцию.

Н а рис. 6 показан процесс сужения интервала исследования:

Рис. 6. Процесс сужения интервала исследования.

Последний N–й расчёт определяет интервал длиной l, в котором находится экстремум целевой функции.

Метод золотого сечения

З олотое сечение проводит деление отрезка АВ на две неравные части так, чтобы было справедливо соотношение (рис. 7).

Рис. 7

Метод золотого сечения позволяет сужать отрезок [a, b] каждый раз вычисляя лишь одно значение F(x), а не два, как в методе дихотомии.

Данный метод реализуется следующим алгоритмом:

1. Находим коэффициент дробления k=(√5-1)/2 отрезка [a, b].

2. Находим абсциссу х₁=a + (1-k)*(b-a) и вычисляем F(x₁).

3. Находим абсциссу х₂=a + k*(b-a) и вычисляем F(х₂).

4. Проверяем выполнение условия |x₂-x₁|<E, где E – заданная погрешность вычисления x_n. Если это условие выполняется, вычисляем x_n = (x₁+ x₂)/2 и F(x_n), после чего останавливаем счёт с выдачей значений x_m и F(x_n). Если данное условие не выполняется, идём к п.5.

5. Проверяем условие F(x₁) < F(x₂). Если оно выполняется, полагаем, а = х₁, х₁ = х₂ и F(x₁) = F(x₂), после чего идём к п.3. и п.4.

Если F(x₁) ≥ F(x₂), полагаем b = x₂, x₂ = x₁, f(x₁) = f(x₂), после чего выполняем п.2 и п.4

Использование ппп Eureka и Excel при решении задач оптимизации

Использование ППП Eureka для поиска экстремумов функций одной переменной.

Для поиска максимумов функций одной переменной необходимо в окне Edit набрать

$|__|max(F)

y(x)=

F=y(x)

В окне Solution будет выдано решение

F=

x=

Перед решением задачи весьма полезно оценить вид функции, экстремум которой необходимо найти и уточнить интервал x, в котором этот экстремум находится. Для этого достаточно воспользоваться командой Plot в позиции Graf основного меню. Из вида графика сделать вывод о правильности решения.

Использование ППП Excel для поиска экстремумов функций одной переменной.

Для поиска максимумов функций одной переменной необходимо:

Вызвать Подбор параметра, с помощью команды в меню Сервис. Окно Подбор параметра состоит из трех полей:

- Установить целевую ячейку, в котором ставится ссылка на ячейку с формулой (Y);

- Равной – выбираем максимальному значению;

- Изменяя ячейки, в которой ставится ссылка на ячейку с изменяемым параметром (первая граница, а интервала (а,в)).

После нажатия кнопки OK, появляется окно, Результаты поиска решения, сохраняем найденное решение. Полученное решение:

Содержание отчета

1. Содержательная постановка задачи.

2. Исходные данные.

3. Краткое описание методов.

4. Блок схема подпрограмм и блок схема головного (или управляющего) модуля.

5. Листинг подпрограмм и управляющего модуля.

6. Распечатка полученных результатов.

7. Распечатка результатов в Excel и Эврика.

Пример выполнения лабораторной работы

Дана функция y = -2x² + 3x + 50.

Найти оптимальное значение функции y двумя способами: методом «золотого сечения» и методом «половинного деления». Заданный интервал измерения x (0;1), точность вычисления E = 0.001.

БЛОК-СХЕМА

Р

1

ис. 8. Блок схема алгоритма (общая и процедура решения по методу половинного деления):

где а, b - нижняя и верхняя границы изменения х;

е - точность вычислений;

dih - процедура вычисления методом половинного деления;

zolot - процедура вычисления методом золотого сечения.

Рис. 9. Блок схема процедуры решения по методу золотого сечения, функция.

ПРОГРАММА НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ QBASIC

DECLARE SUB zolot (a!, b!, E!, xmax!)

DECLARE SUB dih (a!, b!, E!, xmax!)

DECLARE FUNCTION f! (x!)

CLS

INPUT "введите значения отрезка a="; a

INPUT "введите значения отрезка b="; b

INPUT "введите погрешность вычисления Eps="; E

REM метод дихотомии или половинного деления

CALL dih(a, b, E, xmax)

PRINT "Значения max по методу дихотомии"

PRINT "при X="; xmax

PRINT "значение функции Y(xmax)="; f(xmax)

a = 0

b = 1

PRINT "Значение max по методу золотого сечения"

CALL zolot(a, b, E, xmax)

PRINT "при X="; xmax

PRINT "значение функции Y(xmax)="; f(xmax)

END

SUB dih (a, b, E, xmax)

DO UNTIL ABS(b - a) < 2 * E

x1 = (a + b - E) / 2

x2 = (a + b + E) / 2

IF f(x1) > f(x2) THEN

b = x2

ELSE

a = x1

END IF

LOOP

xmax = (a + b) / 2

END SUB

FUNCTION f (x)

f = -2 * x ^ 2 + 3 * x + 50

END FUNCTION

SUB zolot (a, b, E, xmax)

k = (SQR(5) - 1) / 2

x1 = a + (1 - k) * (b - a)

x2 = a + k * (b - a)

DO UNTIL ABS(x2 - x1) < E

IF f(x1) < f(x2) THEN

a = x1

x1 = x2

ELSE

b = x2

x2 = x1

END IF

x1 = a + (1 - k) * (b - a)

x2 = a + k * (b - a)

LOOP

xmax = (x1 + x2) / 2

END SUB