27.Методика вивчення площі круга та його частин.

Питання про площу круга вперше розглядається у 5 кл. Вписавши і описавши навколо даного круга квадрати, учнів переко­нують, що 2R² <S < 4R², і роблять висновок: «Приблизно площа круга дорівнює 3R². Можна довести, що S= «=πR ²». Корисно показати учням, як наближено можна визначити площу круга за допомогою

палетки, або як з розріза­ного на кілька секторів круга скласти фігуру, приблизно схожу на прямокутник

Оскільки основа такого «прямокутника» дорівнює половині довжини кола, а висота — його радіусові, томаємо:

Ще раз повертаються до цієї теми у 8 класі. Тут відмічають,що площа круга S менша від площі , описаного навколо цього правильного n-кутника, але більша від площі S₂ правильного n-кут-ника, вписаного в даний круг.Якщо позначити радіус даного кола буквою R, а периметр вписаного в нього правильного n-кутника буквою р, то неважко показати, що ,

При досить великих п периметр р як завгодно мало відрізняється від довжини кола С, а — від одиниці, бо кут при збільшенні п може стати як завгодно малим. Отже, ліва і права частини написаної вище подвійної нерівності як завгодно мало відрізняються від , що можливо тільки за умови .Таким чином

Окремої формули для визначення площі кругового сектора можна не запам'ятовувати. А якщо потрібно знайти, наприклад, площу сектора, радіус якого R, а кут 60°, учні можуть міркувати так. Кут 60° менший від кута 180° у 3 рази, тому площа даного сектора менша від площі, півкруга теж у 3 рази. Отже, шукана плаща

28.Методика вивчення теми: ”Трикутники”.

З трикутником учні знайомі ще з молодших класів, а в 5 кл. учні уже дет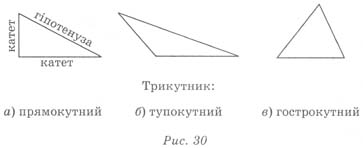 альніше розглядають тему трикутник і його види. Для цього можна намалювавши на дошці усі види трикутників, а учні в зошитах, вимірявши транспортиром кути трикутників можна дати кожному трикутнику означення.

Я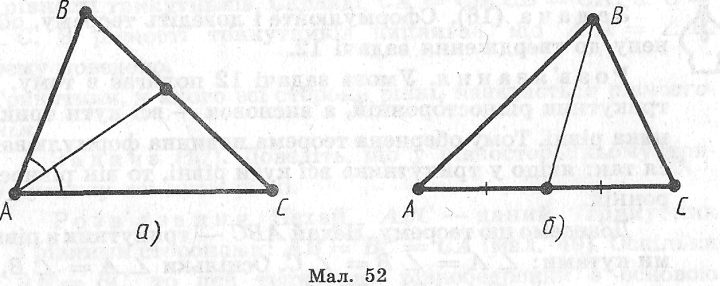 кщо один із кутів трикутника прямий, то трикутник прямокутний (рис. 30, а); якщо один із кутів тупий - тупокутний (рис. 30, б); якщо всі три кути гострі - гострокутний (рис. 30, в). Трикутник, дві сторони якого рівні, називається рівнобедреним (АС = ВС на рисунку 31, а). Третя сторона - основа, рівні сторони - бічні сторони. Трикутник, три сторони якого рівні (АС = ВС = АВ на рис. 31, б), називається рівностороннім.

А вже у 7 кл. учні знайомляться з означенням трикутника. Трикутником називається фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки. Точки називаються вершинами трикутника, а відрізки — його сторонами.

На малюнку 21 ви бачите трикутник з вершинами А, В, С і сторонами АВ, ВС, АС. Трикутник позначається його вершинами. Кутом трикутника АВС при верши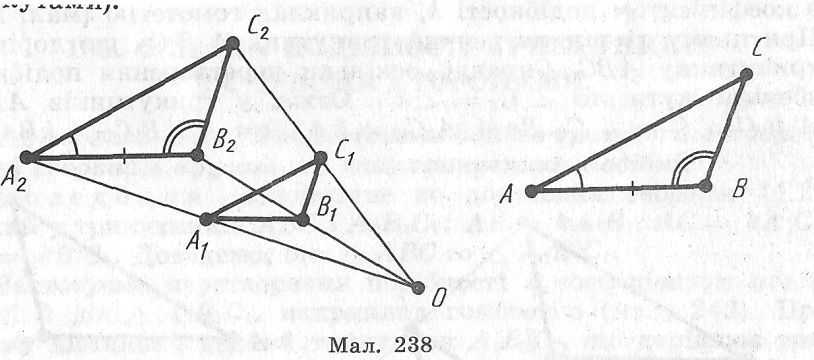 ні А називається кут, утворений півпрямими АВ і АС. Так само означаються кути трикутника при вершинах В і С. Два відрізки називаються рівними, якщо вони мають однакову довжину. Два кути називаються рівними, якщо вони мають однакову кутову міру в градусах. Трикутники називаються рівними, якщо в них відповідні сторони рівні і відповідні кути рівні. При цьому відповідні кути мають лежати проти відповідних сторін. Далі учнів знайомлять з ознаками рівності трикутників.

Висотою трикутника, опущеною з даної вершини, називає­ться перпендикуляр, проведений з цієї вершини до прямої, що містить протилежну сторону трикутника.

На малюнку 51 ви бачите два трикутники, у яких проведено висоти з вершин В і В. На малюнку 51, а основа висоти лежить на стороні трикутника, на малюнку 51, б — на продовженні сторони трикутника. Бісектрисою трикутника, проведеною з даної вершини, називається відрізок бісектриси кута трикутника, що сполучає цю вершину з точкою на протилежній стороні (мал. 52, а). Медіаною трикутника, проведеною з даної вершини, називає­ться відрізок, що сполучає цю вершину із серединою протилеж­ної сторони трикутника (мал. 52, б)

Далі розглядається теорема про суму кутів трикутників.

Теорема. Сума кутів трикутників = 180°. Д-ня: Нехай ABC — даний трикутник. Проведемо через вершину В пряму, паралельну прямій АС. Візьмемо на ній точку D так, щоб точки А і D лежали по різні боки від пря­мої ВС (мал. 78).

Кути DBC і АСВ рівні як внутрішні різносторонні при пере­тині паралельних прямих АС і BD січною ВС. Тому сума кутів трикутника при вершинах В і С дорівнює куту ABD.

А сума всіх трьох кутів трикутника дорівнює сумі кутів ABD і ВАС. Оскільки ці кути внутрішні односторонні для паралель­них АС і BD і січної АВ, то їх сума дорівнює І80°.

Далі учні вивчають все про прямокутній трикут.

Трикутник називається прямокутним, якщо він має прямий кут. Оскільки сума кутів трикутника дорівнює 180°, то в прямокутному трикутнику тільки один прямий кут. Два інших кути прямокутного трикутника гострі. Сума гострих кутів прямокутного трикутника дорівнює 180° — 90° = 90°.

Сторона прямокутного трикутника, що лежить проти прямого кута, наз. гіпотенузою, дві інші сторони наз. катетами

Ознаки подібності трикутників

1. Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то такі трикутники подібні.

Д-ня: Нехай у трикутників ABC і маємо < А = <. , < B= < . Доведемо, що Δ АВС = Δ А₁В₁С₁.Нехай . Застосуємо до трикутника Δ А₁В₁С₁перетворення подібності з коефіцієнтом подібності k, наприклад гомотетію (мал. 238). При цьому дістанемо деякий трикутник , що дорівнює трикутнику ABC. Справді, оскільки перетворення подібності зберігає кути, то Отже, у трикутників ABC і А₂В₂С₂: . Далі = k А₁В₁= АВ. Отже, трикутник А ВС дорівнює трикутнику А₂В₂С₂ за другою ознакою (за стороною і прилеглими до неї кутами). Оскільки трикутники А₁В₁С₁ і гомотетичні, і отже, подібні, а трикутники А₂В₂С₂ і ABC рівні і тому теж подібні, то трикутники А₁В₁С₁ і ABC подібні.

2) Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника та кути, утворені цими сторонами, рівні, то такі трикутники подібні.

3) Якщо три сторони одного трикутника пропорційні трьом сторонам іншого трикутника, то такі трикутники подібні

Теорема Піфагора У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

Д-ня. Нехай ABC — даний прямокутний трикутник з прямим кутом С. Проведемо висоту CD з вершини прямого кута С (мал. 149). За означенням косинуса кута

Звідси АВ∙AD = . Аналогічно . Звідси

АВ·BD = . Додавши рівності почленно і врахувавши, що AD + DB = АВ, дістанемо:

АС² + ВС² = АВ (AD + DB) = АВ². Теорему доведено.