
- •1. Приклади груп. Навпрост. Властивості груп. Підгрупи.
- •2.Кільце. Приклади кілець. Найпростіші властивості кілець. Підкільце.
- •3,Гомоморфізм і ізоморфізм груп і кілець.
- •4. Система нат. Ч. Принцип мат. Індукції.Аксіоми Пеано:
- •5. Поле. П-ди полів. Найпростіші властивості полів. Поле рац. Чисел.
- •6.Поля. Впорядковані поля. С-ма дійсних чисел.
- •7.Поле комплексеих чисел. Числові поля. Геометричне представлення комплексних чисел і дії над ними. Тригонометрична форма комплексного числа.
- •8. Векторний простір. Приклади і найпростіші властивості векторного простору. Підпростір.
- •9.Лінійна залежність і незалежність системи векторів. Базис і ранг скінченної системи векторів.
- •11. Базис і розмірність скінченновимірного векторного простору. Підпростори. Лінійні многовиди. Ізоморфізми векторних просторів.
- •12 Основні властивості конруенції в кільці цілих чисел за даним модулем.
- •13. Повна і зведена система лишків. Теорема Ейлера і Ферма.
- •14. Лінійні порівняння з однією змінною.
- •15. Застосування теорії порівнянь до вивчення ознак подільності цілих чисел.
- •16. Перетворення звич. Др. В десятковий і визначення довжини періоду дробу.
- •17. Поліном над полем. Нсд двох поліномів і алгебра Евкліда
- •18. Розклад полінома у добуток незвідних многочленів і його єдність.
- •19.Алгебраїчна замкненість поля комплексних чисел, спряженість коренів поліномів з дійсними коеф., незвідні над полем дійсних чисел поліноми.
- •20. Будова простого алгебр. Розширення. Звільнення від ірраціон. В знаменнику.
5. Поле. П-ди полів. Найпростіші властивості полів. Поле рац. Чисел.
Озн.
Алгеброю назив. пара
 де
де
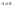 ,
,
 -
мн.,
-
мн.,
 -
м-на операцій заданих на м-ні
-
м-на операцій заданих на м-ні
 .
.
Озн.
Під полем розуміють алгебру
 ,
якщо виконуються властивості:
,
якщо виконуються властивості:
опер. «+» комутативний.
опер. «+» асоціативний
нейтральний елемент відносно опер. «+» належить мн.

Для
 ел.
ел.
 симетр. ел. -
симетр. ел. -

«*» - комутативна.
«*» асоціативна
В мн.
 викон. опер. «÷» крім ділення на 0
викон. опер. «÷» крім ділення на 0Мн.
 належ. хоча б один елем.
належ. хоча б один елем.
 0
0Опер. «+» і «*» пов’язані дистр. законом.
П-ди: Q i R – числа. Мн. N i Z – поля не утв. мн. яка скл. з 2-ох елементів 0 і 1, утв. поле.
Озн. Підмнож. В поля Р наз. підполем поля Р якщо вона сама утв. поле.
Теор.
 числове
поле містить підполе рац. чисел.
числове
поле містить підполе рац. чисел.
Дов.
Задамо довільне числове поле. В ньому
є елемент
0
(вл.8). виберемо один з них. Н-д a.
Оскільки в полі виконується операція
«÷» крім ділення на 0,
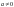 ,
то
,
то
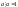 є полем.
є полем.
Припустимо, що
деяке натур. число
 полю.
Так як в полі викон. опер. «+» то і елем.
полю.
Так як в полі викон. опер. «+» то і елем.
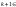 полю.
Тоді за Т мат. індукції поле містить
мн-ну N.
полю.
Тоді за Т мат. індукції поле містить
мн-ну N.
За вл-стю (3) вона
містить елем. 0, а за вл. (4) – для
 елемент
елемент
 числове
поле включає мн-ну цілих чисел Z.
рац.
число можна подати у вигляді дробу
числове
поле включає мн-ну цілих чисел Z.
рац.
число можна подати у вигляді дробу
 ,
де
,
де
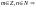 числове
поле в силу вл.7 містить всі дроби виду
числове
поле в силу вл.7 містить всі дроби виду
 ,
де
,
де
 ,
які після скорочення подаються у вигляді
,
які після скорочення подаються у вигляді
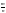 .
Оскільки числове поле містить всі рац.
числа. Оск. сама пл-на
.
Оскільки числове поле містить всі рац.
числа. Оск. сама пл-на
 чисел є числовим полем, то
чисел є числовим полем, то
 числове
поле містить підполе рац. чисел.
числове
поле містить підполе рац. чисел.
6.Поля. Впорядковані поля. С-ма дійсних чисел.
Озн.
М-на
М наз. полем, якщо в ній введено дві
операції «+» і «*»
, тобто
для

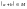 і
і
 ,
які задов. вл-сті:
,
які задов. вл-сті:
1. опер. «+» комутативний.
2. опер. «+» асоціативний
3. в мн.
М
 нейтр.
елем. відносно «+»
нейтр.
елем. відносно «+»
4.
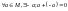
5. «*» - комутативна.
6. «*» асоціативна
7. Ь –
така, в якій
 елем.
елем.

8. в мн.
М визнач. опер. «÷» крім
 на 0
на 0
9. опер.
«+» і «*» пов’язані дистрибутивним
законом

П-ди полів. Мн. рац. та дійсних чисел з визн. на них операц. «+» і «*».
Озн.
Алг. структура наз. впорядкована ним
відношенням «менше» якщо для елем. мн
 викон. такі умови:
викон. такі умови:
1.
 або
або
 або
або
 або
або

2.
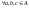 ,
якщо
і
,
якщо
і
 та
та

Озн.
Впорядковане поле
 наз. системою раціональних чисел. якщо
головна мн-на З співпадає з мн. рац.
чисел.
наз. системою раціональних чисел. якщо
головна мн-на З співпадає з мн. рац.
чисел.
Озн.
Поле
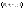 наз. впорядкованою системою дійсних
чисел, якщо головна мн. R є мн. дійсних
чисел.
наз. впорядкованою системою дійсних
чисел, якщо головна мн. R є мн. дійсних
чисел.
Впорядковані поля - задані на впорядкованих системах.
впорядковані системи – система нат. чисел Z, R, Q.
7.Поле комплексеих чисел. Числові поля. Геометричне представлення комплексних чисел і дії над ними. Тригонометрична форма комплексного числа.
Озн.
Множина М наз. полем, якщо в ній введено
дві операції + і *, тобто
a,b
 М,
a*b
М,
a+b
М,
які задовільняють властивості:
М,
a*b
М,
a+b
М,
які задовільняють властивості:
a,b М: a+b=b+a;
a,b,c М: (a+b)+c=a+(b+c);
нейтральний елемент відносно +;
a М: -а: а+(-а)=0;
a,b М: ab=ba;
a,b,c М: (ab)c=a(bc);
хоча б один елемент ≠ 0;
В множині М визначена операція «÷» крім ÷ на 0;
a,b,c М: (a+b)c=aс+bc;
Позначимо через С множину всеможливих пар комплексних чисел. Введемо в С операції + і *: (a;b)+(c;d)=(a+c;b+d); (a;b)·(c;d)=(ac-bd;ad+bc). Легко переконатись, що так введена операція комутативна, асоціативна, дистрибутивна.
Доведемо дистрибутивність:
((a;b)+(c;d))(x;y)=(a+c;b+d)(x;y)=((a+c)x-(b+d)y; (a+c)y+(b+d)x)=(ax+cx-by-dy; ay+cy+bx+dx)=((ax-by)+(cx-dy);(ay+bx; cy+dx)=(a;b)(x;y)+(c;d)(x;y).
Нейтральним
елементом відносно + буде пара (0;0).
Симетричним елементом буде пара (-a;-b).
Очевмдно, що
пара (a;b) для якої
 буде відмінний від 0 елемент. Ми показали,
що так введені операції + і * задовільняють
властивості поля. Множина С наз. полем
комплексних чисел.
буде відмінний від 0 елемент. Ми показали,
що так введені операції + і * задовільняють
властивості поля. Множина С наз. полем
комплексних чисел.
Легко
переконатись, що (0;1) є розв’язком
рівняння
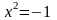 : (0;1)2=(0;1)(0;1)=(0-1;0+0)=(-1;0)=
-1. Позначимо (0;-1)=і, тоді
пару
(a;b) можна подати у вигляді
(a;b)=(а;0)+(0;b)=а+bі. Запис комплексного числа
у вигляді а+bі наз. алгебраїчною формою
комплексного числа.
: (0;1)2=(0;1)(0;1)=(0-1;0+0)=(-1;0)=
-1. Позначимо (0;-1)=і, тоді
пару
(a;b) можна подати у вигляді
(a;b)=(а;0)+(0;b)=а+bі. Запис комплексного числа
у вигляді а+bі наз. алгебраїчною формою
комплексного числа.
Озн. Підмножина Р поля Р наз. підполем, якщо вона сама утв. Поле.
Озн. підполе поля комплексних чисел наз числовим полем. Числові поля: множини, компл. числа, дійсні і рац числа.
Алгебраїчна форма комплексного числа a+bi
Кожному
компл. числу на коорд. площині відповідає
т.(a;b). Цю точку можна задати в полярних
координатах: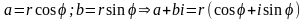 —
це тригонометрична форма комплнксного
числа.
—
це тригонометрична форма комплнксного
числа.
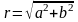 -модуль;
— аргумент; Re(z)=a- дійсна, Im(z)=b- уявна
частина.
-модуль;
— аргумент; Re(z)=a- дійсна, Im(z)=b- уявна
частина.
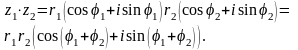
 ;
;
 ,
,

Властивості компл. чисел: 1. a+ib=c+id : a=c, b=d. 2.(a+ib)+(c+id)=(a+c)+i(b+d). 3.(a+bi)-(c+di)=(a-c)-i(b+d). 4. (a+bi)(c+di)=(ac-bd)+(ad+bc)i.
5.
 .6.
.6.
 .
7.
.
7.
 .
8.
.
8.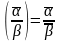 .
9.
.
9.
 .
10.
.
10.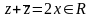 .
.
