1. Приклади груп. Навпрост. Властивості груп. Підгрупи.

Озн. Не порожня множ А , на якій задано бінарну операцію *, унарну операцію -1 наз. групою, якщо викон. такі властивості:

1) бінарна операція *- асоціативна;

2) е – правий нейтральний елемент відносно операції * в множ А;

3) для 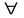елемента правий симетричний елемент , що .

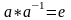Приклади. Z з операцією +; множ парних чисел відносно операції +; множ, яка склад з одного нуля також утворює групу відносно операції +.

Властивості груп:

1. правий симетричний елемент є одночасно і лівим елементом;

2. правий нейтральний елемент є одночасно і лівим нейтральним елементом;

3. нейтральний елемент єдиний;

4. для 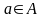симетричний елемент єдиний;

5. для в групі кожне з р-нь а*х=b, y*a=b має єдиний розв’язок;

6. властивість скорочення. для з а*с=b*с а=b, таке саме з с*а=с*b;

7. для групи з рівності а*b=а b=е, таке саме з b*с=с;

8. ;

9. для 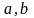групи з рівності а*b=е .

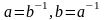Дов. 1) .

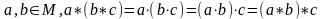2) , .

3) а*е=а

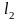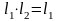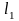Дов. 3). Припустимо, що - нейтральні елементи. Оскільки правий нейтральний елемент, то в силу 2) , тому можна записати = . Оскільки також нейтральний елемент, то він є лівим нейтральним елементом, тому . Отже, = , тобто

= , що суперечить припущенню, тому нейтральний елемент єдиний.

Дов. 9). З 3) - * . З другої сторони , тоді за 8) .

Озн.Підгрупою групи наз під алгебра цієї групи (приклад): множ парних чисел з операцією + є під алгеброю адитивної алгебри Z.

Озн.Відображу h групи <A, *, -1> в групу <B, *,-1> наз гомоморфізмом.

Теор. Підгрупа групи є знову група. Нейтральний елемент групи є нейтральним елементом підгрупи.

2.Кільце. Приклади кілець. Найпростіші властивості кілець. Підкільце.

Озн. Кільцем наз. алгебраїчну структуру <K, +, *> з двома алгебраїчними операціями + і *заданими на всій множині К, яка задов. умови:

а) відносно операції «+» стр. <K,+> утв. адитивну абелеву групу, тобто: 1) ;

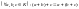2) ;

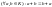3) ;

4) ;

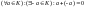б) Відносно операції множення стр. <K, *> утв. групу ;

в) Операції «+» і «*» пов’язані розподільним законом .

Якщо операція множення переставна, то кільце комутативне, якщо в кільці 1 відносно «*», то кільце К наз кільцем з 1.

Приклади: 1) Множина Z утв. кільце (з1).2)Множина М_n — усіх матриць n-го порядку з дійсними елем. утв. кільце.3)Множина усіх неперервних функцій на відрізку 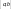;4) Множина Z_m –усіх класів лишків утв. кільце

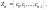
Властивості:1) В кільці існує єдиний нейтральний, нульовий та одиничний елемент . 2)В скінченних сумах і добутках можна довільно розставляти дужки. 3)Для кожного елемента кільця протилежний і якщо обернений, то він теж єдиний. 4) –(a+b)=(-a)+(-b).5) має єдиний розв’язок х=b+(-а) його наз. різницею а і b і позначають b-а.

6) 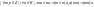.7) .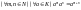

8)

- дистриб. властивість множення відносно віднімання. Згідно озн. різниці . 9) ця властивість є вірною тільки для числових кілець.

Озн. Ненульові елементи а і b, для яких аb=0 наз. дільниками нуля, а-лівий, b-правий дільник.

Озн. Комутативне кільце без дільників нуля наз. областями цілісності.

10) Рівності можна скорочувати не на дільники нуля: , а-недільник о, . 11)

Озн. Непорожня підмножина К₀ кільця К наз. підкільцем, якщо вона сама утв. кільце відносно операцій заданих в кільці К.

Теор. Підмножина є його підкільцем т. і т. т., коли вона задовільняє умови: ; ; .

Дов.: Якщо К₀ –підкільце К, то К₀ задов. згідно озн., усім аксіомам кільця, внаслідок чого умови 1-3 виконуються, то в силу умов 1-2 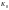утв. підгрупу адитивної групи кільця, внаслідок чого вона задовольняє усім аксіомам групи. Це означає,що задов. усім аксіомам кільця, отже -підкільце кільця К.