2.2. Редактор графиков

Графический редактор MathCAD обеспечивает построение различных видов графиков: в декартовой и полярной системе координат, трехмерные поверхности, графики уровней и т.п.

Для построения графиков в подменю График (позиция Вставка) имеются шаблоны типов графиков. Большинство параметров, необходимых для построения графиков, задается автоматически. Вид окна системы с подменю вставки шаблонов показан на рис. 7.

Рис. 7- Вид подменю вставки шаблона графики

Другим способом выбора шаблона типа графика является использование панели Графики, вызываемой щелчком по соответствующей кнопке панели Математика.

Перед построением графика в декартовой системе координат надо задать ранжированную переменную - аргумент функции, например х, указав диапазон его изменения и шаг изменения d. Шаг задается путем указания начального значения переменной х0, а затем, через запятую, значения х 0+d. После этого через двоеточие указывается конечное значение х. Затем надо объявить функцию (или функции) и только после этого вывести шаблон двумерного графика. Незаполненный шаблон представляет собой пустой прямоугольник с местами ввода данных в виде маленьких черных

прямоугольников. В средние шаблоны данных по оси абсцисс надо поместить имя переменной, а по оси ординат - имя функция. Если в одном шаблоне строят графики нескольких функций, то их имена вводят через запятую. Примеры построения графиков трех функций показаны на рис. 8.

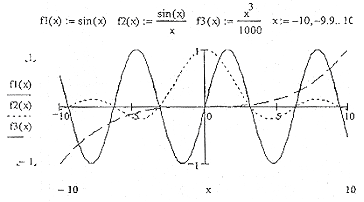
Рис.8. Построение графиков в декартовой системе координат

Для построения графика в автоматическом режиме вычислений достаточно вывести курсор за пределы графика. Если вид построенного графика не удовлетворяет пользователя, можно применить опции изменений. Для этого следует дважды щелкнуть мышью в области графика и в появившемся окне (рис.9) произвести изменение опции.

Окно опций формата графика имеет четыре вкладки, позволяющие менять основные параметры графиков и осуществлять различные установки:

Оси X-Y - установки параметров осей (нанесение сетки с заданным шагом, нумерацию по осям и т.д.);

След - установки параметров линий графиков: метка символа, вид линии (сплошная, пунктирная), толщина и цвет линии каждого графика, установка опции показа или скрытия аргумента у oceй;

Метка - служит для установки пояснительных надписей по осям X и Y, ввода надписей;

Умолчание - возврат к стандартным установкам.

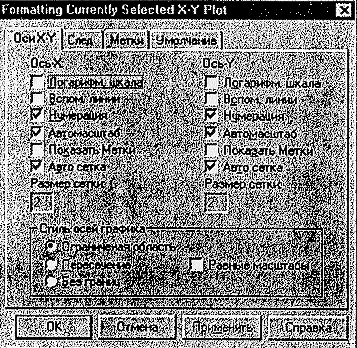
Рис. 9. Окно опций формата графика

При построении графика в полярной системе координат каждая точка задается углом W и модулем радиус-вектора R(W) . График функции обычно строится в виде линии, которую описывает конец радиус-вектора при изменении угла W в определенных пределах (чаще всего от 0 до 2π). После вывода, шаблона надо ввести W в шаблон снизу, a R(W) - справа (рис. 10).

Для построения графика поверхности вида Z(x,y) требуется задать вид функции и диапазоны изменения обеих переменных х и у, затем представить значения аппликат Z матрицей М и задать формат трехмерного графика (рис.11).

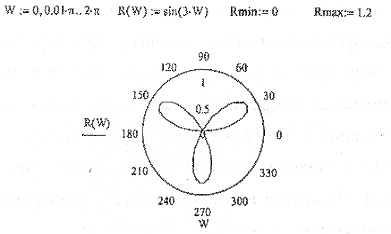
Рис. 10. График, построенный в полярной системе координат

Рис. 11. Задание и построение графика поверхности

При появлении шаблона графика поверхности в единственный шаблон данных, расположенный в нижнем левом углу, заносится имя матрицы со значениями аппликат поверхности.

Наглядность представления графика поверхности зависит от множества факторов: масштаба, углов поворота , фигуры,

использования закраски и т.д. Для настройки параметров рекомендуется использовать операцию установки формата.

Еще один широко распространенный тип графиков для представления поверхностей - контурный график представления поверхностей с помощью линий равного уровня. Тип графика задается с помощью соответствующей кнопки панели Графики (рис.12). Численные значения уровней для разных кривых графика представлены рядом цифр около линий уровня.

Рис. 12. Контурный график поверхности

Распространенной формой представления поверхностей является также представление ее рядом трехмерных столбиков, высота которых определяется значением координат Z(x,y). Для этого используется операция Трехмерная гистограмма (рис.13). Подобные графики широко применяются при представлении сложных статистических данных.

Рис. 13. Построение трехмерной диаграммы