1.6. Динамика. Колебательное движение.

32. Сила, возвращающая материальную точку в положение равновесия: , где - коэффициент квазиупругой силы.

33. Энергия колебательного движения:

а) кинетическая энергия

;

б) потенциальная энергия

;

в) полная энергия

.

Примеры решения задач.

Пример 1. Кинематическое уравнение материальной точки имеет вид x = A + Bt + Ct³ (A = 2 м, В = 3 м/с, С = –0,5 м/с³). Найти координату х₂, скорость ₂ и ускорение а₂ в момент времени t = 2c. Каковы средние значения скорости и ускорения за первые 2с движения?

Решение. Координату х₂ найдем, подставляя в уравнение движения числовые значения коэффициентов и времени t:

х₂ = (2+32 – 0,58) = 4 м. (1)

Мгновенная скорость равна производной от уравнения движения:

 = , ₂ = -3 м/с. (2)

Ускорение точки определим как производную от уравнения для скорости:

а = . (3)

Средняя скорость находится так: <>=x/t, где х – разность координат для моментов времени:

t₁ = 0 и t₂ = 2c, x = x₂-x₁, t = t₂-t₁ = 2c. (4)

Координата х₂ – известна, координата х₁ для момента времени t₁ = 0 х₁ = 2 м.

Вычисляем: <> = 2 м/с.

Среднее ускорение определим как:

<a> = ;  = ₂ – ₁, t = t₂-t₁. (5)

Скорость ₂ для момента времени t₂ = 2 c уже вычислена, скорость для момента времени t₁=0 ₁=3 м/с. Отсюда <a>= –3 м/с².

Пример 2. Тело брошено со скоростью ₀=20 м/с под углом  = 30º к горизонту. Пренебрегая сопротивлением воздуха, найти скорость тела, а также его нормальное и тангенциальное ускорение через t = 1.5 c после начала движения. На какое расстояние l переместится за это время тело по горизонтали и на какой окажется высоте h?

Решение. Если тело движется с постоянным ускорением а = g, его скорость и перемещение определяются векторными уравнениями:

. (1)

М ы не знаем в какой точке траектории будет тело через 1,5 с после начала движения – на восходящей или нисходящей ветвях параболы. Предположим, что оно находится в точке М (рис. 1). Введем координатные оси, направленные по горизонтали (ОХ) и вертикали (ОY) и совместим начало координат с положением тела в начальный момент времени. Тогда, подставив в уравнения

_x=_ox+a_xt, _y=_oy+a_yt,

x= _oxt+a_xt²/2, y= _oyt+a_yt²/2 (2)

Рис. 1

значения а_х=0, а_у = -g, _ох = _ocos, _ох = _osin, x = x, y = y и учитывая, что проекция скорости тела в точке М на ось ОY направлена вниз, получаем:

_x=_ocos;

x=_ocost;

-_y=_osin-gt;

y=_osint – . (3)

Искомые величины l и h равны координатам х, y точки М в момент t=1,5с.

l = x = _ocost = 20,00,871,5 м = 26 м. (4)

h = y = _osin – gt²/2 = [20,00,51,5-9,8(1,5)²/2] м = 4,0 м. (5)

Скорость  в точке М найдем через ее проекции:

(6)

Для определения нормального и тангенциального ускорения учтем, что полное ускорение тела, движущегося в поле земного тяготения, есть не что иное как ускорение g силы тяжести. Разложив вектор g на составляющие по нормальному и касательному направлению к траектории в точке М – получим (рис. 1):

а_n = gsin = g( ), (7)

а_r = gcos = g( ), (8)

где  – угол между вертикалью и касательной к траектории в точке М.

Подставив вместо величин _x , _y,  их значения, получим:

, (9)

. (10)

Пример 3. Молотком, масса которого m₁ = 1.0 кг, забивают в стену гвоздь массой m₂ = 75 г. Определить К.П.Д. () удара молотка.

Решение. Коэффициент полезного действия (К.П.Д.) есть отношение полезной энергии к затраченной:

 = . (1)

Полезной будем считать кинематическую энергию молотка и гвоздя после их взаимодействия W_полезн = , где u – совместная скорость молотка и гвоздя (взаимодействие считаем неупругим). Затраченной энергией является кинетическая энергия молотка до удара W_затр = , где  – скорость молотка до удара. Систему молоток-гвоздь можно приближенно считать замкнутой и применить закон сохранения импульса:

, (2)

где m₁ – импульс молотка до удара; (m₁+m₂)u – импульс системы молоток-гвоздь после удара.

Из выражения (2) находим скорость u: u = .

Подставляя в (1) выражения для энергии, определяем :

= = 0.93.

Пример 4. Пружина жесткостью k = 500 Н/м сжата некоторой силой F. При дополнительном сжатии еще на l = 6 см совершена работа А = 12 Дж. Определить величину силы F первоначального сжатия пружины.

Решение. Согласно закону Гука величина упругой силы F связана с абсолютной деформацией |х| по модулю:

|F| = k|x|, (1)

где k – коэффициент жесткости.

Работа упругой силы при сжатии от l до l + l

A = (2)

Теперь, пользуясь соотношением (1) можно записать

|F| = kl, (3)

где l – первоначальное сжатие пружины.

Значение l находится из выражения (2):

l = . (4)

Отсюда

F = k . (5)

Произведя вычисления, получим: F = 185 Н.

Пример 5. Круглая платформа радиуса R = 1.0 м, момент инерции которой J = 130 кгм², вращается по инерции вокруг вертикальной оси, делая n₁ = 10 об/сек. На краю платформы стоит человек, масса которого m = 70 кг. Сколько оборотов в секунду n₂ будет совершать платформа, если человек перейдет в ее центр? Момент инерции человека рассчитывать как для материальной точки.

Решение. Согласно условиям задачи платформа с человеком вращается по инерции, т.е. результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы платформа-человек выполняется закон сохранения импульса:

L₁ = L₂. (1)

Подсчитаем начальный момент импульса L₁ (человек стоит на краю платформы) и конечное его значение L₂ (человек стоит в центре платформы).

L₁ = J₁₁ = (J + mR²) 2n₁, (2)

где mR² – момент инерции человека, J₁ = J + mR² – начальный момент инерции системы, ₁ – ее начальная угловая скорость.

L₂ = J₂₂ = J2n₂, (3)

где J₂ и ₂ – конечные момент инерции и угловая скорость системы. Здесь учтено, что момент инерции человека, стоящего в центре платформы, равен 0.

Решая систему уравнений (1) – (3), получаем:

n₂ = n₁(J + mR²)/J,

n₂ = 1.5 об/с.

Пример 6. Физический маятник представляет собой стержень длиной l = 1 м и массой 3m с прикрепленным к одному из его концов обручем диаметром d = l и массой m. Горизонтальная ось OZ проходит через середину стержня перпендикулярно ему. Определить период Т колебаний такого маятника (рис. 2).

Р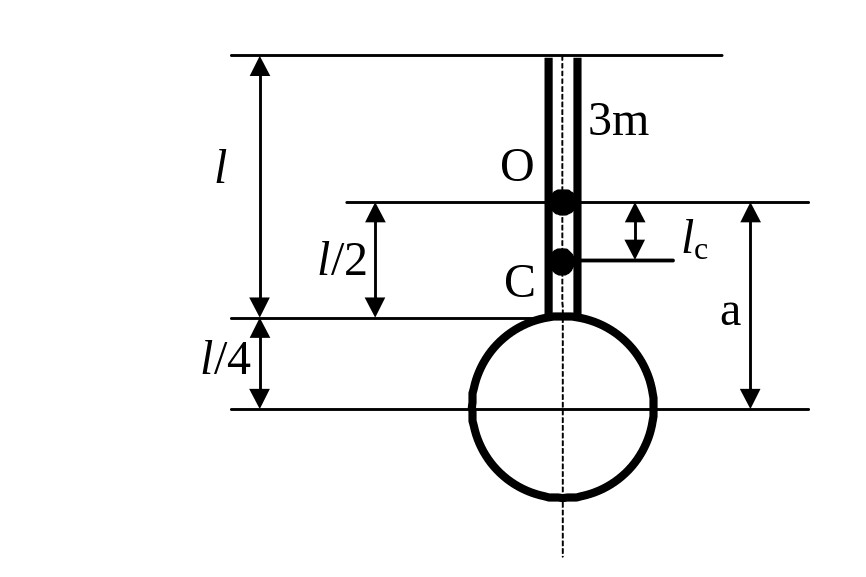 ешение. Период колебаний физического маятника определяется по формуле:

, (1)

Рис. 2

где J – момент инерции маятника относительно оси колебаний; М – его масса; l_c - расстояние от центра масс маятника до оси колебаний.

Момент инерции маятника равен сумме моментов инерции стержня J₁ и обруча J₂:

J = J₁ + J₂. (2)

J₁ определяется по формуле :

J₁ = m₁l². (3)

В данном случае m₁ = 3m и J₁ = ml². (4)

Момент инерции обруча найдем, воспользовавшись теоремой Штейнера J = J₀ + m₂a² (где a – расстояние между осями; J₀ – момент инерции относительно оси, проходящей через центр масс параллельно заданной оси).

Момент инерции обруча равен:

J₂ = m₂(l/4)²+m₂(3l/4)² = 5/8m₂l²; J₂ = 5/8ml², (m₂=m). (5)

Подставив выражения (4) и (5) в формулу (2), найдем момент инерции маятника относительно оси вращения:

J = 1/4ml² +5/8ml² = 7/8ml². (6)

Расстояние l_c от оси маятника до его центра масс равно:

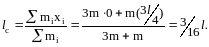(7)

Подставив в формулу (1) выражения J, l_c и массы маятника (М = 3m + m = 4m), найдем период его колебаний:

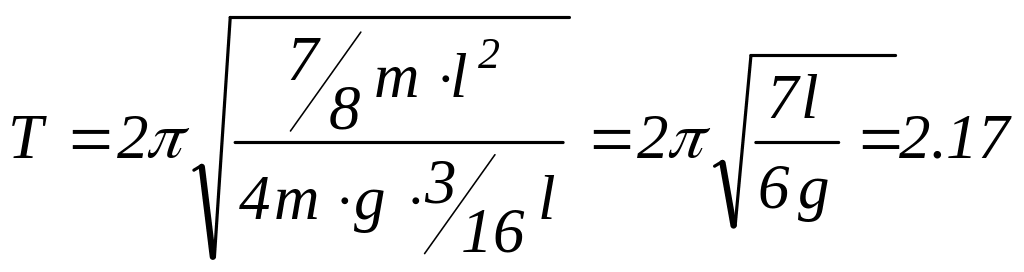(с).

П ример 7. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выраженных уравнениями х = 2sin(t); y = –cos(t) (смещения в сантиметрах). Найти уравнение траектории точки и построить ее на чертеже. Показать направление движения точки. Определить скорость и ускорение точки в момент t = 0.5 с.

Рис. 3

Решение. Так как циклические частоты слагаемых колебаний одинаковы, траекторией точки будет эллипс. Исключив время t из двух заданных уравнений, получим:

. (1)

Это каноническое уравнение эллипса с полуосями а = 2 см и b = 1 см (рис. 3). Чтобы определить направление движения точки, учтем, что в момент времени t = 0 имеем х = 0, y = –1 см, и, следовательно, точка находится в положении А. При возрастании t увеличивается также x, значит, точка движется по траектории против часовой стрелки. Скорость точки  при ее движении по эллипсу равна векторной сумме скоростей _x и _y в слагаемых колебаниях. Поскольку эти колебания взаимно перпендикулярны, то . (2)

Аналогично определяем искомое ускорение: , (3)

где а_х и а_у – ускорения точки в слагаемых колебаниях.

Скорость и ускорение определяются по формулам:

_x = 2cost, _y = sint, (4)

а_x = –2²sint, a_y = ²cost.

Подставив эти выражения в формулы (2) и (3), найдем:

,

и, взяв t = 0.5 с, получим:

=3.14 см/с;

а=19.7 см/с.

варианты	Номера задач по темам: "Механика", "Молекулярная физика и термодинамика"
1	101	141	121	161	201	241	221	261
2	102	142	122	162	202	242	222	262
3	103	143	123	163	203	243	223	263
4	104	144	124	164	204	244	224	264
5	105	145	125	165	205	245	225	265
6	106	146	126	166	206	246	226	266
7	107	147	127	167	207	247	227	267
8	108	148	128	168	208	248	228	268
9	109	149	129	169	209	249	229	269
10	110	150	130	170	210	250	230	270
11	111	151	131	171	211	251	231	271
12	112	152	132	172	212	252	232	272
13	113	153	133	173	213	253	233	273
14	114	154	134	174	214	254	234	274
15	115	155	135	175	215	255	235	275
16	116	156	136	176	216	256	236	276
17	117	157	137	177	217	257	237	277
18	118	158	138	178	218	258	238	278
19	119	159	139	179	219	259	239	279
20	120	160	140	180	220	260	240	280
21	121	161	101	141	221	261	201	241
22	122	162	102	142	222	262	202	242
23	123	163	103	143	223	263	203	243
24	124	164	104	144	224	264	204	244
25	125	165	105	145	225	265	205	245
26	126	166	106	146	226	266	206	246
27	127	167	107	147	227	267	207	247
28	128	168	108	148	228	268	208	248
29	129	169	109	149	229	269	209	249
30	130	170	110	150	230	270	210	250
31	131	171	111	151	231	271	211	251
32	132	172	112	152	232	272	212	252
33	133	173	113	153	233	273	213	253
34	134	174	114	154	234	274	214	254
35	135	175	115	155	235	275	215	255
36	136	176	116	156	236	276	216	256
37	137	177	117	157	237	277	217	257
38	138	178	118	158	238	278	218	258
39	139	179	119	159	239	279	219	259
40	140	180	120	160	240	280	220	260

Таблица выбора заданий по физике по темам: "Механика", "Молекулярная физика и термодинамика" для студентов заочной формы обучения