Тема 8. Модели сетевого планирования и управления

Назначение и области применения сетевого планирования и управления. Сетевая модель и ее основные элементы. Порядок и правила построения сетевых графиков. Упорядочение сетевого графика. Понятие о пути. Временные параметры сетевых графиков. Сетевое планирование в условиях неопределенности. Коэффициент напряженности работы. Анализ и оптимизация сетевого графика. Оптимизация сетевого графика методом «время-стоимость».

Задачи для самостоятельного решения

Задача 8.1. Найти продолжительность выполнения комплекса работ, временные характеристики событий и работ (в скобках указана продолжительность работ). Построить сетевой график.

Сделать деревянный ящик (работу выполняет один человек). Разместить доски в соответствии с размерами ящика (15 мин.); разрезать доски (12 мин.); склеить части ящика (40 мин.); прибить к крышке ящика петли (8 мин); подождать пока ящик высохнет, и вытереть его (15 мин.); петли с крышкой прибить к ящику (10 мин).

Задача 8.2. Найти продолжительность выполнения комплекса работ, временные характеристики событий и работ (в скобках указана продолжительность работ). Построить сетевой график.

Заменить колесо машины (работу выполняют два человека). Достать из багажника домкрат и инструменты (40 с.); снять диск с колеса (30 с.); освободить колесо (50 с); поставить домкрат под машину (26 с.); поднять машину (20 с.); из багажника взять запасное колесо (25 с.); снять гайки и колесо (20 с.); установить запасное колесо на ось (10 с.); завинтить (не сильно) гайки на оси (15 с.); опустить машину и собрать домкрат (25 с.); поставить домкрат обратно в багажник (10 с.); завинтить гайки на оси до конца (12 с); положить плохое колесо и инструменты в багажник (40 с.); поставить на место диск колеса (10 с.).

Задача 8.3. Для сетевого графика (рис.1) найти все полные пути, критический путь; рассчитать ранние и поздние сроки свершения событий, начала и окончания работ; определить резервы времени полных путей и событий, резервы времени (полные, частные резервы первого вида, свободные и независимые) работ и коэффициенты напряженности работ.

.

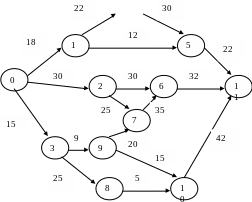
Рис. 1. Сетевой график по выполнению проекта

Задача 8.4. Как изменится срок выполнения проекта (см. рис. 1), резервы времени работ и событий, коэффициенты напряженности работ, если увеличить продолжительность работы t (9,10) на величину:

а). Полный резерв времени работы - Rп (9,10);

б). Частный резерв времени работы первого вида - R1 (9,10);

в). Частный резерв времени работы второго вида или свободный резерв времени работы - Rс (9,10);

г). Независимый резерв времени работы - Rн (9,10)?

Задача 8.5. В таблице указаны оценки времени выполнения работ сетевого графика, данные ответственными исполнителями и экспертами.

№ п/п	Работа (i,j)	Оценки времени выполнения работы, сутки
		оптимистическая (i,j)	пессимистическая (i,j)	наиболее вероятная (i,j)
1	(1,2)	5	9	6
2	(1,3)	2	7	5
3	(1,4)	4	10	8
4	(3,4)	9	14	11
5	(2,5)	7	13	10
6	(4,5)	1	4	3

Необходимо: 1) построить сетевой график; 2) определить средние (ожидаемые) значения продолжительности работ; 3) определить критический путь и его длину.

Полагая, что продолжительность критического пути распределена по нормальному закону, найти: 1) вероятность того, что срок выполнения комплекта работ не превысит 17 суток; 2) максимальное значение продолжительности выполнения проекта, которое можно гарантировать с надежностью 0,95.

Задача 8.6. По данным таблицы необходимо: 1) построить сетевой график; 2) определить критический путь и стоимость проекта при минимально возможных значениях продолжительности всех работ; 3) найти минимальную стоимость проекта при том же сроке его завершения; 4) рассчитать и построить оптимальную зависимость стоимости проекта от продолжительности его выполнения, используя в качестве первоначального варианта сетевого графика: а) план с максимальными значениями продолжительности всех работ и соответственно минимальной стоимостью проекта; б) план, полученный в результате выполнения п.3.

Работа	Нормальный план выполнения работы, сутки		Срочный план выполнения работы, сутки		Коэффициент затрат на ускорение работы
	min	max	min	max
(1,2)	4	5	2	15	5
(1,3)	4	3	2	11	4
(1,4)	12	150	9	180	10
(2,3)	6	11	5	30	19
(2,4)	7	18	6	30	12
(3,4)	10	10	8	20	5
(3,5)	24	147	19	212	13
(4,5)	10	4	7	25	7
(5,6)	3	2	2	5	3