Тема 5. Элементы теории игр

Понятие об игровых моделях. Платежная матрица. Нижняя и верхняя цена игры. Решение игр в смешанных стратегиях. Геометрическая интерпретация игры 2х2. Приведение матричной игры к задаче линейного программирования.

Задачи для самостоятельного решения

Задача 5.1. Предприятие выпускает скоропортящуюся продукцию, которую может сразу отправить потребителю (стратегия А1), отправить на склад для хранения (стратегия А2) или подвергнуть дополнительной обработке (стратегия А3) для длительного хранения.

Потребитель может приобрести продукцию: немедленно (стратегия В1), в течение небольшого времени (В2), после длительного периода времени (В3).

В случае стратегий А2 и А3 предприятие несет дополнительные затраты на хранение и обработку продукции, которые не требуются для А1, однако при А2 следует учесть возможные убытки из-за порчи продукции, если потребитель выберет стратегии В2 или В3.

Определить оптимальные пропорции продукции для применения стратегий А1, А2, А3, руководствуясь «минимаксным критерием» (гарантированный средний уровень убытка) при матрице затрат, представленной в таблице.

Стратегии предприятия (Ai)	Стратегии потребителя (Bj)
	В1	В2	В3
А1	2	5	8
А2	7	6	10
А3	12	10	8

Задача 5.2. Магазин может завести в различных пропорциях товары трех типов (А1, А2, А3); их реализация и прибыль магазина зависят от вида товара и состояния спроса.

Предполагается, что спрос на товары может иметь три состояния (В1, В2, В3) и не прогнозируется. Определить оптимальные пропорции в запуске товаров из условия максимизации средней гарантированной прибыли при следующей матрице прибыли.

Тип товара	Спрос
	В1	В2	В3
А1	20	15	10
А2	16	12	14
А3	13	18	15

Задача 5.3. Для следующих платежных матриц определить нижнюю и верхнюю цены игры, минимаксные стратегии и оптимальные решения игры, если существует седловая точка.

А ). Б).

Найти решения игр путем сведения их к задаче линейного программирования, используя представленные платежные матрицы.

Тема 6. Модели нелинейного программирования

Классические методы оптимизации (методы определения экстремумов, метод множителей Лагранжа). Модели выпуклого программирования: производная по направлению и градиент, выпуклые функции, задача выпуклого программирования. Приближенное решение задач выпуклого программирования методом кусочно-линейной аппроксимации. Методы спуска. Приближенное решение задач выпуклого программирования градиентным методом. Понятие о параметрическом и стохастическом программировании.

Задачи для самостоятельного решения

Задача 6.1. Предприятие для производства продукта А расходует два средства в количестве и соответственно. Факторы производства считаются взаимозаменяемыми.

Объем производства, выраженный в натуральных единицах, является функцией затрат производства и представлен следующей производственной функцией: где - затраты факторов, - цены этих факторов, которые составили 1 и 2 соответственно. Совокупные издержки выражаются формулой , причем b = 4.

Требуется при данных совокупных издержках определить такое количество факторов производства, которое максимизирует объем продукции z.

Задача 6.2. Найти глобальный экстремум (наибольшее и наименьшее значения) объема продукции z в области системы неравенств, представленных ниже и дать геометрическое решение.

А ). 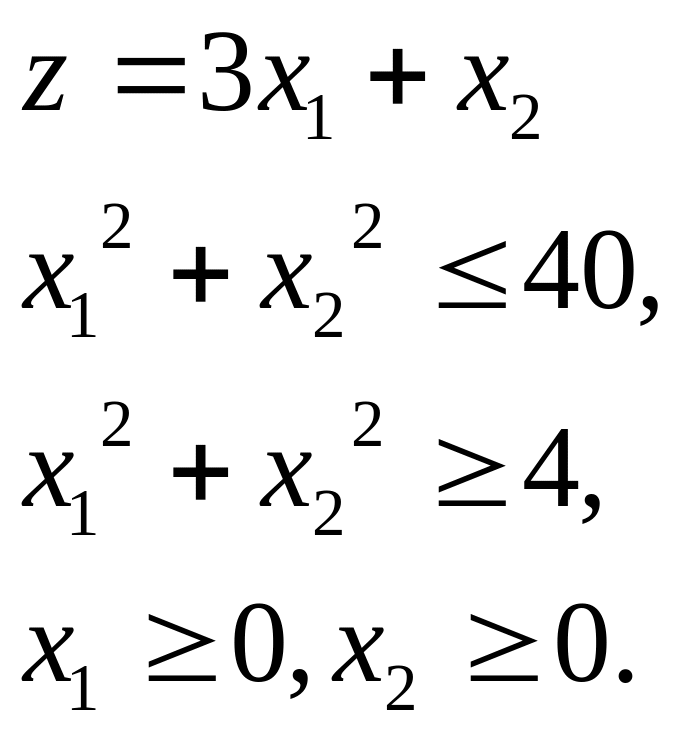Б).