Плотный индекс

Пусть по каким-либо причинам невозможно упорядочить основной файл F по ключу К. Построим дополнительный файл FD по правилу [24]:

1) записи файла FD имеют формат FD(K, Р), где К – поле, принимающее значение ключа записи основного файла F; Р – указатель на эту запись;

2) записи файла FD упорядочены по полю К.

Полученный файл называется плотным индексом. Он строится почти так же, как и неплотный индекс. Различие заключается в том, что для каждого значения ключа К в файле FD имеется отдельная запись, а в неполном индексе - только для значения ключа первой записи блока.

Пример плотного индекса представлен на рис. 11.4. Над плотным индексом можно также построить В-дерево.

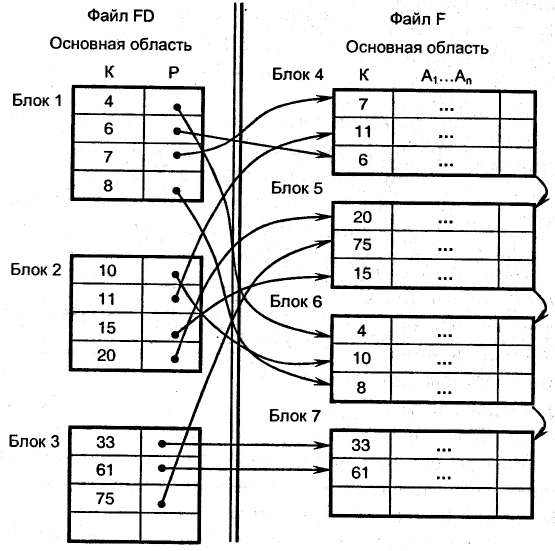
Рис.11.4. Пример плотного индекса

Инвертированный файл

В рассмотренных выше способах индексирования данных расчет делался на поиск по значению ключевого поля. Но часто требуется осуществить выборку данных по значениям неключевых полей. В этом случае неключевые поля также должны быть проиндексированы (т.е. для каждого из них строится особый индекс). Индексы, построенные для неключевых полей используются при организации многоаспектного поиска. Широко распространены на практике методы многоаспектного поиска по инвертированным файлам. Пусть имеется основной файл F, упорядоченный либо неупорядоченный по значениям вторичного ключа К_i. Строится дополнительный файл FD_i по правилу [24]:

1) записи файла FD_i имеют формат FD_i(K_i, P) где K_i – поле, принимающее значение вторичного ключа К_i записи основного файла; Р – указатели на записи основного файла F, имеющие данное значение вторичного ключа К_i;

2) записи файла FD_i упорядочены по полю K_i.

Построенный дополнительный файл FD. Называется инвертированным. В этом случае об основном файле F говорят, что он инвертирован по полю К_i. Количество записей в инвертированном файле FD_i определяется количеством значений вторичного ключа К_i в записях основного файла F. Пример инвертированного файла по полю К₂ для основного файла F приведен на рис. 11.5. Рассмотренный способ организации инвертированного файла предполагает использование записей переменной длины. Инвертированный файл можно организовать и с помощью записей фиксированной длины, если в каждой записи инвертированного файла выделять фиксированное число полей для указателей Р. Если фиксированного числа поле для некоторых записей окажется недостаточно, то организуется еще дополнительный служебный файл для хранения неуместившихся цепочек указателей.

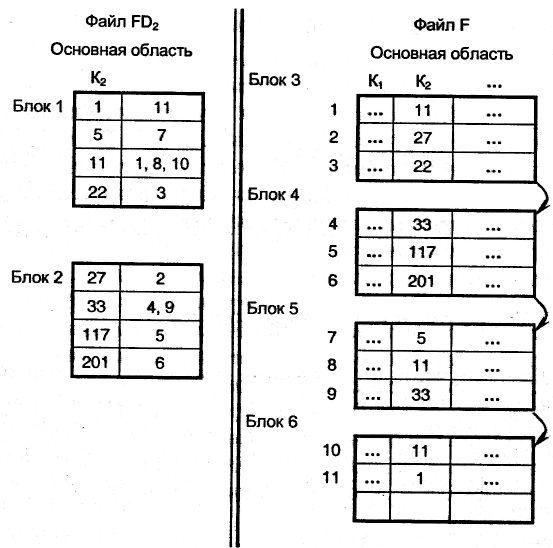
Рис.11.5. Пример инвертированного файла

Поскольку записи инвертированного файла упорядочены по значению ключа K_i, то для поиска записей можно использовать любой из рассмотренных выше методов поиска в упорядоченном файле (например, бинарный поиск или В-дерево). Чтобы выполнить многоаспектный поиск по n ключам, необходимо построить п инвертированных файлов [24].

Лекция 12. Реляционная модель данных Понятие отношениях

Реляционная модель данных была предложена Е.Ф. Коддом в конце 1960-х и получила к настоящему времени широкое распространение и популярность. Этому способствовали два ее существенных достоинства: 1) однородность представления данных в модели, которая обусловливает простоту восприятия ее конструкций пользователями базы данных, и 2) наличие развитой математической теории реляционных баз данных, которая обусловливает корректность ее применения [18].

В основе реляционной модели данных лежит понятие отношения, которое задается списком своих элементов и перечислением их значений. Рассмотрим пример на рис.12.1.На нем представлено расписание движения автобусов по маршруту "Москва - Черноголовка - Москва". Налицо определенная структура. Каждый включенный в расписание рейс имеет свой номер, время отправления и время в пути. Расписание может быть представлено таблицей. Заголовки колонок таблицы носят название атрибутов. Список их имен носит названия схемы отношения. Каждый атрибут определяет тип представляемых им данных, который вместе с областью его значений называется доменом. Вся таблица целиком называется отношением, а каждая строка таблицы носит название кортежа отношения. Таким образом, отношение можно представить в виде двумерной таблицы.

Рис. 12.1.  Расписание движения автобусов по маршруту "Москва - Черноголовка - Москва" как отношение

Подходы к определению понятия отношения могут быть различными. Математически отношение может быть определено как множество кортежей, являющейся подмножеством декартова произведения фиксированного числа областей (доменов). В результате получаем, что в каждом кортеже должно быть одинаковое число компонент (атрибутов) и значение каждого из них выбирается из некоторого определенного домена.

Введем ряд математических определений, связанных с понятием отношения.

Определение 1. Декартово произведение Пусть D₁, D₂, ..., D_n - произвольные конечные множества, не обязательно различные. Декартовым произведением этих множеств называется множество вида . Пример:

Определение 2. Схема отношения

Пусть - имена атрибутов. Схемой r отношения R называется конечное множество имен атрибутов .

Определение 3. Отношение

Отношением со схемой r на конeчных множествах D₁, D₂,…, D_n называется подмножество R декартового произведения .

Элементы отношения (d₁, d₂, ..., d_n), как уже упоминалось выше, называются кортежами. О каждом отношении, являющимся подмножеством декартового произведения , можно сказать, что оно имеет арность n. Кортеж (d₁, d₂, ..., d_n) имеет n компонентов. Для обозначения кортежа применяется и сокращенная форма записи d₁, d₂, ..., d_n. Использование понятия декартового произведения для определения отношения в реляционной модели данных делает модель конструктивной. На математическом языке это означает, что все остальные понятия модели определяются в рамках строго математического построения на базе декартового произведения.

Табличная форма представления отношения была введена в целях популяризации модели среди неподготовленных пользователей баз данных. Трактовка реляционной теории на уровне таблиц скрывает ряд определений, важных для понимания как теории реляционных баз данных, так и языка манипулирования данными, моментов.

Во-первых, атрибуты разных отношений могут быть определены на одном домене, так же как и атрибуты одного отношения. Это очень важное обстоятельство, позволяющее устанавливать связи по значению между отношениями. Во-вторых, множество математически по своему определению не может иметь совпадающих элементов, и, следовательно, кортежи в отношении можно различить лишь по значению их компонент. Это тоже очень важное для модели обстоятельство: никакие два кортежа не могут иметь полностью совпадающих компонент. Таким образом, в реляционной модели полностью исключается дублирование данных о сущностях реального мира! В-третьих, заметим, что схема отношения также есть множество, что позволяет работать с ними с помощью теоретико-множественных операций. Это является важным моментом для построения теории проектирования реляционных схем баз данных.

Существует определенное различие между математическим определением отношения и действительным хранением отношений в памяти компьютера. По определению, отношение не может иметь два идентичных кортежа. Однако СУБД, поддерживающие реляционную модель данных, хранят отношения в файлах операционной системы компьютера. Размещение отношений в файлах операционной системы допускает хранение идентичных кортежей. Если не используется специальная техника (контроль целостности по первичному ключу), то обычно большинство промышленных СУБД допускают хранение двух идентичных кортежей в базе данных.

С математической точки зрения однородность реляционной модели, о которой упоминалось выше, состоит в том, что схема отношения является постоянной, иначе говоря, каждая строка таблицы имеет один и тот же формат. С другой стороны, предполагается, что каждая строка таблицы представляет некую сущность реального мира или связь между ними. Обладают ли сущности реального мира такой однородной структурой, является вопросом, на который должен ответить аналитик или эксперт-пользователь. Решение о пригодности использования реляционной модели для моделирования данных конкретной предметной области решается руководителем ИТ-проекта и аналитиками[18].