Последовательное распределение памяти

Последовательное распределение – простой и естественный способ хранения линейного списка. В этом случае узлы списка размещаются в последовательных элементах памяти (рис.10.1) [24].

При последовательном распределении вектор данных логически отделен от описания структуры хранимых данных. Например, если структура данных представляет собой линейный список (файл записей фиксированной длины), то описание структуры хранится в отдельной записи и содержит:

а) N – размер вектора данных, т.е. количество элементов списка записей;

б) т – размер элемента списка, т.е. размер записи, например, в байтах;

в) β – адрес базы, указывающий на начало вектора данных в памяти.

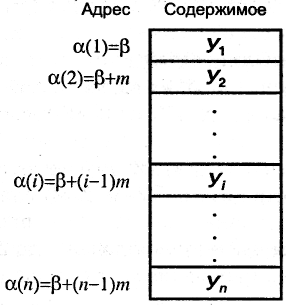
Рис. 10.1. Пример последовательного распределения памяти для представления линейного списка

В этом случае адрес каждой записи можно вычислить с помощью адресной функции, отображающей логический индекс, идентифицирующий запись в структуре, в адрес физической памяти

(10.1)

В случае линейного списка адресная функция состоит из операций смещения и масштабирования. Любые отношения, которые можно выразить на языке целых чисел, можно истолковать как отношения между элементами памяти, получая при этом всевозможные варианты структур.

В качестве примера (из [24]) рассмотрим реализацию с помощью линейного списка при последовательном распределении памяти для логической структуры типа регулярного двоичного дерева (рис. 10.2). Идея способа заключается в том, что начиная с элемента памяти α(1), делают его корнем дерева, размещают там данные, соответствующие узлу У₁. В элементах памяти α(2) и α(3) размещают непосредственных потомков узла У₁ – узлы У₂ и У₃, и т.д. В общем случае, непосредственные потомки узла У_k размещаются по адресам: α(2k) и α(2k+1). Адресная функция имеет вид

(10.2)

где k – номер узла древовидной структуры; β – базовый адрес; т – размер элемента памяти, который требуется для хранения данных узлов дерева (каждый узел представляет собой запись фиксированной длины). По дереву, которое при этом получается, можно двигаться в обоих направлениях, так как от узла У_k можно перейти к его потомкам, удвоив k (или удвоив k и прибавив единицу). Можно двигаться к узлу, являющемуся исходным для узла У_k, разделив k пополам и отбросив дробную часть. Адрес соответствующего узлу элемента памяти определяется по адресной функции.

Рассмотрим еще один способ реализации, который применим только для двоичных деревьев. Если для представления двоичного дерева используется вектор памяти от элемента i до элемента j включительно, то корень дерева размещается в элементе памяти с адресом

(10.3)

где   – знак округления до ближайшего меньшего целого.

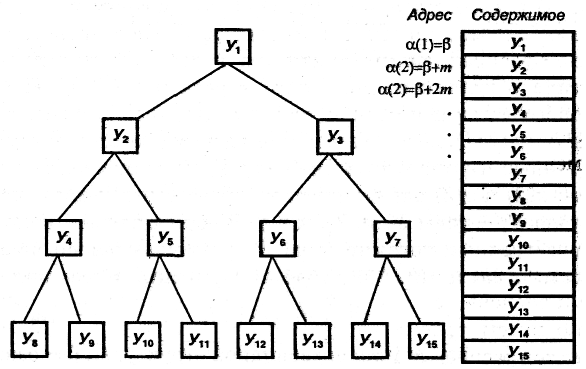
Рис.10.2. Пример реализации структуры типа регулярного двоичного дерева с помощью линейного списка

Корень дерева размещается в середину вектора. В элементах памяти от i-гo до (m-1)-гo включительно размещается левое поддерево. В элементах памяти от (m+1)-го до j-го включительно размещается правое поддерево. Аналогично процесс повторяется для размещения каждого поддерева. Приведенный способ позволяет реализовать двоичное сбалансированное дерево.

Существует ряд других способов представления древовидных структур [6, 19, 24]. С помощью приемов, основанных на свойствах целых чисел, можно с помощью последовательного распределения организовать в памяти некоторые сетевые структуры. Однако для представления сложных сетевых структур требуются более гибкие методы построения в памяти компьютера, которые невозможно получить с помощью последовательного распределения памяти. В этом случае используется связанное распределение памяти.