Зависимости соединения

Многозначные зависимости представляют собой попытку выделения декомпозиций без потери информации, сохраняющих это свойство для всех отношений с заданной схемой. Однако MV-зависимости не полностью в этом смысле адекватны. Отношение может иметь нетривиальную декомпозицию без потерь на три схемы, но не обладать таким свойством для любых двух из них.

Пример 14. Отношение r со схемой ABC на рис. 10.1 разлагается без потерь на схемы АВ, АС и ВС (рис.10.2). Однако r не удовлетворяет никаким нетривиальным MV-зависимостям и, следовательно, не имеет декомпозиций без потери информации на пары R₁, R₂, такие, что R₁ ≠ (A, В, С) и R₂ ≠ (A, В, С).

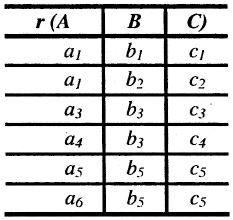
Рис. 10.1. Пример отношения

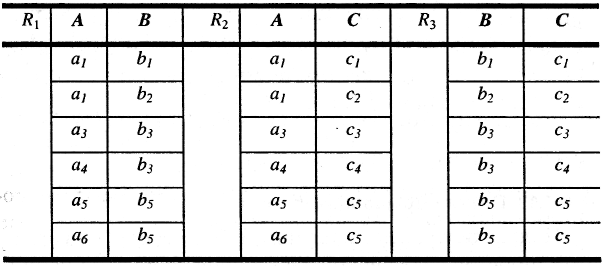
Рис. 10.2. Пример декомпозиции

Пусть R={R₁, ..., R_p} – множество реляционных схем над U. Отношение r(U) удовлетворяет зависимости соединения (J-зависимости) *[R₁, R₂, ..., R_p], если r разлагается без потерь на R₁, R₂, ..., R_p.

Пример 15. Отношение r на рис. 10.1 удовлетворяет J-зависимости *[АВ, АС, ВС].

Необходимым условием выполнения в отношении r(U) J-зависимости *[R₁, R₂, ..., R_p] является равенство U=R₁R₂...R_p. Из определения также видно, что MV-зависимость является частным случаем J-зависимости. Отношение r(R) удовлетворяет MV-зависимости X→→Y тогда и только тогда, когда r разлагается без потерь на XY и XZ, где Z=R-(XY). Условие совпадает с J-зависимостью *[XY, XZ]. С другой стороны, зависимость соединения *[R₁, R₂] имеет тот же смысл, что MV-зависимость R₁  R_{2 →→} R₁.

Для J-зависимости можно привести определение, аналогичное определению MV-зависимости [14]. Пусть r удовлетворяет зависимости *[R₁, R₂, ..., R_p]. Если r содержит кортежи t₁, t₂, ..., t_p, такие, что для всех i, j

то r содержит кортеж t, такой, что t(R_i) = t_i(R_i), 1 ≤ i ≤ p.

Пятая нормальная форма

Целью поиска декомпозиций без потери информации является устранение избыточности из отношений. В терминах поиска декомпозиций без потерь 4НФ не является наилучшим решением.

J-зависимость *[R₁, R₂,..., R_p] над R называется тривиальной, если она удовлетворяется в любом отношении r(R) [14].

J-зависимость соединения *[R₁, R₂, ..., R_p] приложима к реляционной схеме, если R=R₁R₂...R_p.

Пусть R – схема отношения и F – множество F- и J-зависимостей над R. Схема R находится в пятой нормальной форме (5НФ) относительно F, если для каждой J-зависимости *[R₁, R₂, ..., R_p], выводимой из F и приложимой к R, J-зависимость тривиальна или каждое R_i является сверхключом R [14].

Схема базы данных R находится в пятой нормальной форме относительно F, если в этой форме находится каждая схема R из R.

Приведем еще одно определение 5НФ [14].

Пусть R – схема отношения и F – множество F- и J-зависимостей. R находится в пятой нормальной форме (5НФ) относительно F, если для каждой J-зависимости *[R₁, R₂, ..., R_p], выводимой из F и приложимой к R, зависимость *[R₁, R₂, ..., R_p] выводима из ключевых F-зависимостей в R.

Обобщение этапов нормализации

Упрощенная обобщенная схема этапов нормализации отношений с привязкой к известным нормальным формам, выполняемая на этапе логического проектирования базы данных, представлена на рис. 10.3.

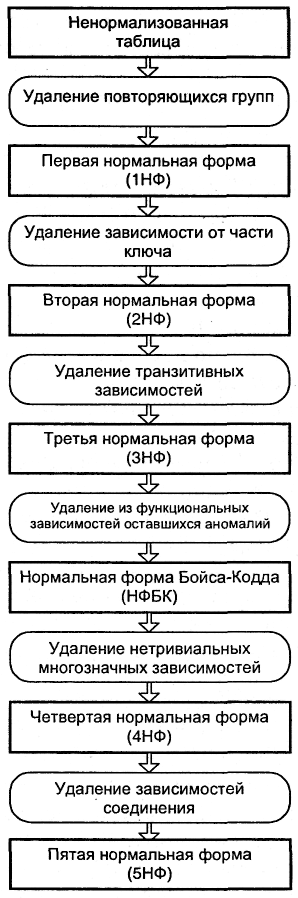
Рис. 10.3. Обобщенная схема процесса нормализации