2.3.6. Метод контурных токов

Метод базируется на 2-м законе Кирхгофа, число независимых уравнений в этом случае (n_в - n_у + 1) вместо n_в уравнений предыдущего метода расчета.

Введем в рассмотрение некоторые токи, называемые контурными, которые замыкаются в независимых контурах (это не физические токи цепи).

Сначала получим уравнения методом контурных токов для простейшей схемы, а затем сформулируем общее правило.

Рассмотрим схему рис. 2.30. В схеме n_в = 3, n_у = 2, число независимых уравнений, составляемых по 2-му закону Кирхгофа равно n_в-n_у+1 = 3-2+1 = 2. В качестве независимых контуров примем два элементарных контура, контурные токи в которых обозначим I₁₁, I₂₂ и направим их по часовой стрелке. Произвольно зададимся положительными направлениями токов в ветвях (физически существующие токи), показанными на рис. . Токи в ветвях выражаются через контурные токи следующим образом, I₁= I₁₁, I₂= I₂₂, I₃= I₁₁ - I₂₂ (a)

Рис. 2.30.

Запишем уравнения по 2-му закону Кирхгофа для 1-го и 2-го контуров. I₁(R₁ + R₂) + I₃R₃ = E₁ - E₃ ,I₂(R₄ + R₅) - I₃R₃ = -E₂ + E₄

Используя (а), получим I₁₁(R₁ + R₂ + R₃) - I₂₂R₃ = E₁ - E₃ ,I₂₂(R₄ + R₅ + R₃) - I₁₁R₃ = -E₂ + E₄ .

Физически (R₁ + R₂ + R₃) – собственное сопротивление 1-го контура; (R₃ + R₄ + R₅) – собственное сопротивление 2-го контура; R₃ – сопротивление общей ветви между 1 и 2 контурами.

Из этого примера видно, что метод контурных токов уменьшил число уравнений в системе до двух вместо трех. Реальные токи в ветвях определяются по соотношениям (а), а напряжения между любыми точками – по закону Ома. Сформулируем правило, по которому можно составить уравнение для контурных токов применительно к схеме, содержащей k контуров. Если I₁₁ , I₂₂ , …, I_kk – контурные токи, то система уравнений будет иметь вид: 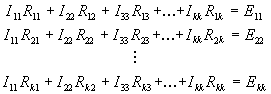, (3.6.1)

где R_ii (сопротивление с одинаковыми индексами) – собственное сопротивление i-го контура (сумма сопротивлений всех ветвей, входящих в контур i); R_ik (сопротивление с разными индексами) – сопротивление ветви, общей между i-м и k-м контурами, если направления контурных токов в общей ветви для контуров i и k совпадают, то R_ik положительно (R_ik >0), если контурные токи направлены в общей ветви встречно, то R_ik отрицательно (R_ik <0); E_ii – алгебраическая сумма ЭДС, действующих в i-м контуре.

Любой контурный ток определяется ,

где  – определитель системы;  _i – определитель  , в котором i-й столбец заменен свободными членами.

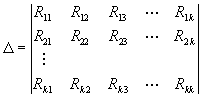
Определитель  симметричен относительно главной диагонали, так как физически R_ik=R_ki.

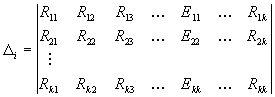i-й столбец.

Наличие источников тока в цепи позволяет уменьшить число уравнений, составленных методом контурных токов до величины n_в - n_у + 1 - N_T , где N_T – число источников тока. При наличии источников тока следует выбрать так независимые контуры, чтобы через каждый источник тока проходил единственный контурный ток. Тогда этот контурный ток равен току источника и для него уравнение составлять не требуется.

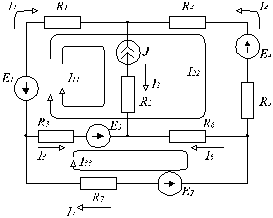Рис. 2.31

Для схемы рис. 2.31 покажем выбор независимых контуров, составим уравнения методом контурных токов и запишем токи в ветвях. В схеме n_в = 6, n_у = 4, следовательно число уравнений, составляемых методом контурных токов, равно n_в - n_у + 1 = 6 - 4 + 1 = 3, а наличие источника тока уменьшает число уравнений до 2 (n_в - n_у + 1 - N_T = 2). Через источник тока должен проходить единственный контурный ток, поэтому выберем контуры следующим образом: 1 – E₁, R₁, J, R₂, E₃, R₃; 2 – E₁, R₁, R₄, E₄, R₅, R₆, E₃, R₃; 3 – R₃, E₃, R₆, E₇, R₇. Направим контурные токи I₁₁, I₂₂, I₃₃ по часовой стрелке. Для первого контура можем записать I₁₁ = -J, знак “минус” появился из-за того, что контурный ток I₁₁ направлен встречно току источника J. Уравнение для второго контура в соответствие с (3.6.1) имеет вид:

I₂₂(R₁+R₄+R₅+R₆+R₃)+(R₁+R₃)I₁₁ - I₃₃(R₃+R₆) = E₁ – E₄ – E₃.

Уравнение для третьего контура:

I₃₃(R₃+R₆+R₇)– I₁₁R₃ – I₂₂(R₃+R₆) = -E₃ – E₇.

Учтем, что I₁₁ = -J и получим систему из двух уравнений с двумя неизвестными I₂₂, I₃₃.

-J(R₁+R₃)+I₂₂(R₁+R₄+R₅+R₆+R₃)– I₃₃(R₃+R₆) = -E₁ – E₄ – E₃

JR₃ – I₂₂(R₃+R₆)+I₃₃(R₃+R₆+R₇) = E₃ – E₇.

Рассчитав контурные токи I₂₂ , I₃₃ , запишем реальные токи в ветвях. Для этого произвольно зададимся направлениями токов в ветвях, например, так как показано на рис. . Ток ветви находится как алгебраическая сумма контурных токов: со знаком “плюс” записываются контурные токи, направления которых совпадают с выбранным направлением тока ветви, со знаком “минус” записываются контурные токи, направление которых противоположено выбранному направлению тока ветви.

I1 = I11+I22 ,	I3 = I33 – I11 – I22 ,	I6 = -I33 ,
I2 = I11 ,	I4 = -I22 ,	I7 = I33 .