3.6 Построение переходных характеристик системы

Расчет переходных характеристик системы в Mathcad выполняют двумя способами: численным интегрированием системы обыкновенных дифференциальных уравнений или символьными обратными преобразованиями Лапласа.

3.6.1 Численное определение переходной характеристики системы

Переходная характеристика системы находится при этом в три этапа:

1. преобразование передаточной функции системы в систему обыкновенных и алгебраических уравнений, общий вид которой:

Y(p)=Z₁(p)a₀+ a_j-1;

pZ₁(p)=Z₂(p);

pZ₂(p)=Z₃(p);

............;

pZ_i(p)=Z_i+1(p);

.............;

pZ_n-1(p)=Z_n(p);

pZ_n(p)=(X(p)- b_k-1),

где Z_i - дополнительные переменные состояния (выходы интеграторов);

2. численное интегрирование полученной системы;

3. вывод результатов в виде графиков или таблиц.

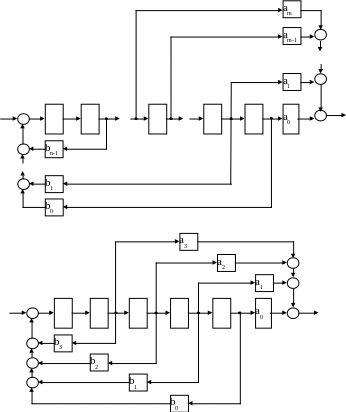
При преобразовании передаточной функции в систему уравнений рекомендуется использовать метод вспомогательной переменной. Для чего строится структурная схема, общий вид которой показан на рисунке 3.6.

Число интегрирующих элементов равно порядку полинома числителя и определяет порядок системы (количество дифференциальных уравнений).

Пример построения системы уравнений для передаточной функции (3.4)

На основе структурной схемы рисунка 3.6 с учетом порядка числителя и знаменателя W(p) детализируется на рисунке 3.7. По схеме рисунка 3.7 составляется система уравнений аналитической модели W(p):

dz₀(t)/dt=z₁(t);

dz₁(t)/dt=z₂(t);

dz₂(t)/dt=z₃(t);

dz₃(t)/dt=[x(t)–z₃(t)b₃–z₂(t)b₂–z₁(t)b₁–z₀(t)b₀]/b₄;

y(t)=z₀(t)a₀+z₁(t)a₁+z₃(t)a₃.

Время переходного процесса находится на основе максимального значения вещественной части вектора корней характеристического уравнения системы:

tп||, где i=1…n.

Оценка жесткости производится с помощью отношением модулей максимального и минимальных значений корней характеристического уравнения:

=.

Задача является плохо обусловленной («жесткой»), если   10⁵.

…

Z_n Z_m Z₂ Z₁

X(p) Y(p)

(-)

…

Рисунок 3.5 – Детализированная структурная схема разложения W(p)

X(p) Z₃ Z₂ Z₁ Z₀ Y(p)

(-)

Рисунок 3.6 – Пример детализации выражения (3.4)

Для численного интегрирования на интервале от tн до tк системы обыкновенных дифференциальных уравнений в виде векторной функции F, у которой начальные условия интегрирования в векторе y0 заданы, используются функции с числом шагов n с максимальным числом промежуточных точек решения k и минимально допустимым интервалом между точками s и погрешностью acc:

1. rkadapt(y0,tн,tк,acc,n,F,k,s) – метод Рунге-Кутта с переменным шагом;

2. Rkadapt(y0,tн,tк,n,F) - метода Рунге-Кутта с переменным шагом;

3. rkfixed(y0,tн,tк,n,F) – метод Рунге-Кутта с постоянным шагом;

4. Bulstoer(y0,tн,tк,n,F) – метод Булирша-Штера.

Для интегрирования на интервале от tн до tк “жестких” систем дифференциальных уравнений в Mathcad используются функции интегрирования с числом шагов n, погрешностью acc для матрицы якобиана J с максимальным числом промежуточных точек решения k, минимально допустимым интервалом между точками s, реализующие:

1. bulstoer(y0,tн,tк,acc,n,F,k,s) –метод Булирша-Штера с переменным шагом;

2. Stiffb(y0,tн,tк,n,F,J) –метод Булирша-Штера с переменным шагом;

3. stiffb(y0,tн,tк,acc,n,F,J,k,s) –метод Булирша-Штера переменным шагом;

4. Stiffr(y0,tн,tк,n,F,J) –метод Розенброка с переменным шагом;

5. stiffr(y0,tн,tк,acc,n,F,J,k,s) –метода Розенброка переменным шагом.

Пример расчета переходной характеристики для системы (3.1).

График строится с помощью шаблона XY Plot

Рисунок 3.7 – Построение переходной характеристики

3.6.2 Символьный расчет переходной характеристики

При этом используется раздел меню Simbolics Главного меню Mathcad, в котором для записанного выражения передаточной функции (для обозначения оператора Лапласа следует использовать символ s вместо p) используется символьная функция обратного преобразования Лапласа invlaplase из подраздела Transform. При этом можно использовать палитру символьных операций.