2. Скорость точки при различных способах задания ее движения

Определение: скоростью точки, отвечающей данному моменту времени, называется векторная физическая величина, полностью характеризующая движение точки в данный момент времени; изображается закрепленным в данной точке вектором.

1.2.1. Скорость точки при векторном способе задания ее движения

Дано:3 пункта векторного способа задания движения точки:

(1.1).

Определить: точки М

Пусть точка при движении по траектории в момент времени t совпадает с точкой М траектории и ее положение определяет радиус-вектор , проведенный в выбранной системе отсчета из неподвижной точки O, а в момент времени (t+ Δt)  с точкой М₁, которой соответствует радиус-вектор , (рис.1.6). Приращение радиус-вектора за промежуток времени Δt составит . Тогда среднее изменение радиус-вектора точки за промежуток времени Δt определяется как отно шение , где  средняя скорость за время Δt.

П риращение радиус-вектора в данный момент времени, равный пределу изменения радиус-вектора точки, когда значение промежутка времени Δt стремится к нулю, называется скоростью точки в момент времени t. Такой предел есть производная от радиус-вектора точки по времени, т.е.

(1.11)

Рис.1.6

Вектор направлен по приращению радиус-вектора точки, т.е.

по направлению секущей ММ₁

При стремлении Δt к нулю секущая в пределе становится касательной к траектории в точке М, поэтому вектор направлен по касательной (рис.1.1 и 1.6).

Таким образом, скорость точки равна первой производной по времени от радиус-вектора точки и всегда направлена по касательной к траектории в сторону движения точки, а ее численное значение определяется модулем . Единица измерения скорости в СИ  метр в секунду (м/c).

Путь S , пройденный точкой по траектории за промежуток времени

Δt = (t₂ – t₁) , можно определить и как предел суммы модулей приращений радиус-вектора точки за малые отрезки времени , на которые разбивается промежуток времени (t₂ – t₁), при условии, что (см. 1.9):

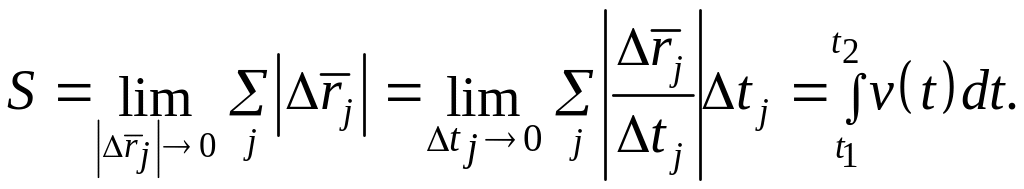(1.12)

 модуль скорости, выраженный в виде функции времени.

1.2.2. Скорость точки при координатном способе задания ее движения

Даны: кинематические уравнения при координатном способе задания движения точки:

, , (1.2).

Определить: точки М.

Имеем (1.11): , = + + . (1.13)

На основании (1.11) и (1.13) скорость точки, при задании ее движения в декартовой системе координат, определяется как

 +  +  . (1.14)

В (1.14) производные , т.е. коэффициенты при ортах

, , , имеют смысл проекций скорости точки на оси декартовой системы координат, т.е.

,  ,  . (1.15)

Таким образом, скорость точки в данном случае представляет собой сумму составляющих векторов, параллельных осям декартовой системы координат (рис.1.2):

,

где ,  ,  , а ее численное значение (модуль) определяется по формуле

. _. (1.16)

Направление вектора определяется значением направляющих косинусов углов, которые составляет этот вектор с осями декартовой системы координат:

, , . (1.17)

Здесь , ,   углы, которые составляет вектор с осями Ox, Oy и

Oz соответственно.