Вращение твердого тела (корабельного на волнении или сухопутного на грунте носителей) вокруг неподвижной точки.

ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

4.1. Выбор осей координат. Углы Крылова (корабельные

углы). Кинематические уравнения корабельного носителя

на волнении

Вращательным движением твердого тела вокруг неподвижной точки называется такое его движение, при котором одна точка твердого тела или неизменно с ним связанная остается неподвижной относительно выбранной системы отсчета. Его еще называют сферическим движением, поскольку траектория любой точки тела лежит на поверхности сферы с центром в неподвижной точке. Примером такого движения служит волчок, у которого остается неподвижной точка опоры.

Число степеней свободы свободно движущегося в пространстве твердого тела равно шести. Если во время движения тела одна его точка остается неподвижной, то число степеней свободы такого тела при его вращении вокруг этой неподвижной точки будет равно трем и для оценки его положения необходимо задать три независимых параметра. Сделать это можно различными способами. Например, А.Н. Крылов в качестве таких параметров предложил так называемые корабельные углы, определяющие положение твердого тела (корабля) относительно системы координат, связанной своим началом с его центром тяжести С (рис.4.1).

За оси неподвижной системы координат приняты CXYZ, а за оси жестко связанные с кораблем – Cxyz (рис.4.1). Ось СХ направлена от кормы к носу корабля, ось CZ – к его правому борту, а ось CY образует с ними правую систему координат (вертикально вверх).

Рис. 4.1

Положение подвижной системы координат Cxyz, неизменно связанной с кораблем, относительно неподвижной CXYZ для каждого момента времени определяется тремя углами Крылова: углом дифферента , углом крена , углом рыскания (рис. 4.2)..

Рис. 4.2

Как видно на рис. 4.2, плоскость CXY пересекает плоскость Cxy по некоторой прямой , образующей угол с осью CX и угол с осью Cx. Плоскость CYZ пересекает плоскость Cхy по линии Cy₁, образующей угол с осью Cy.

Рассмотрим переход от системы CXYZ к системе Cxyz, выполненный

с помощью трех поворотов (рис.4.3).

Рис.4.3

1  Первый поворот системы CXYZ вокруг третьей из координатных осей CZ на угол дифферента , в результате чего получим систему , причем Cz₁=CZ (рис.4.4.1) и (рис.4.5.1);)

1.1) Формулы преобразования координат от CXYZ к связаны следующими соотношениями (рис.4.4.1):

X = x₁ cos   y₁ sin  + 0 ,

Y = x₁ sin  + y₁ cos  + 0 , (4.1)

Z = 0 + 0 + z₁ ,

Рис.4.4.1

1.2)Формулы преобразования координат от CXYZ к в матричной форме (рис.4.5.1):

Рис.4.5.1

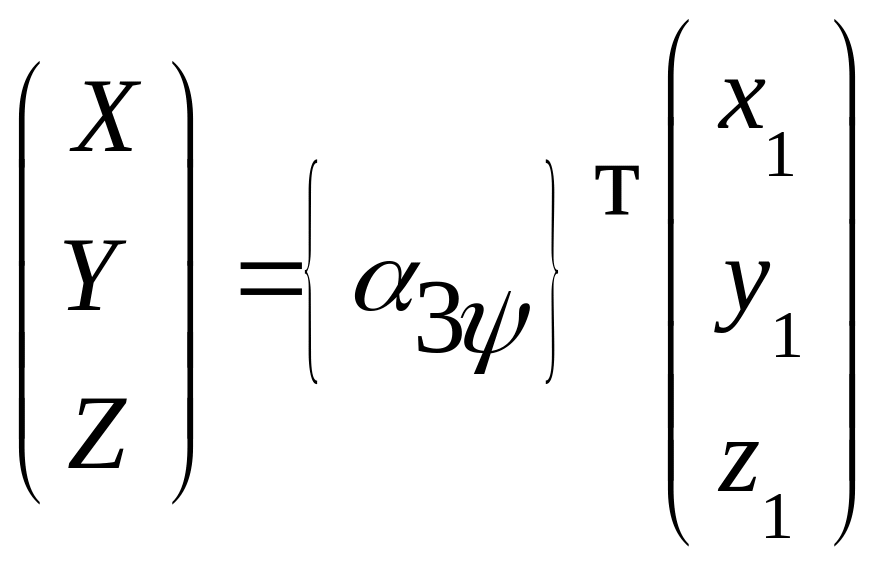или . (4.2)

Здесь  матрица, транспонированная к матрице , описывающей поворот системы CXYZ вокруг третьей из координатной осей оси СZ на угол дифферента  и называется поворотной матрицей:

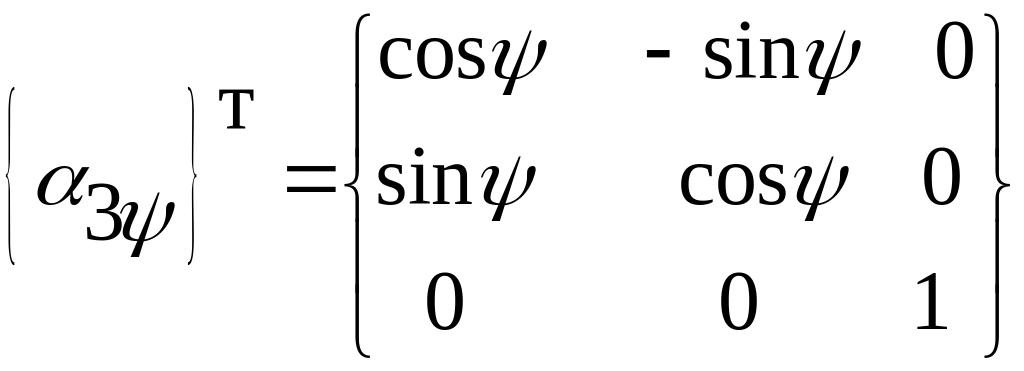; (4.3)

2 Второй поворот системы вокруг первой из координатных осей на угол крена , в результате чего получим систему , при этом , где ось - названа замечательной осью или линией узлов (рис.4.4.2) и (рис.4.5.2*);

2.1) Формулы преобразования координат от системы к системе связаны следующими соотношениями (рис.4.4.2:

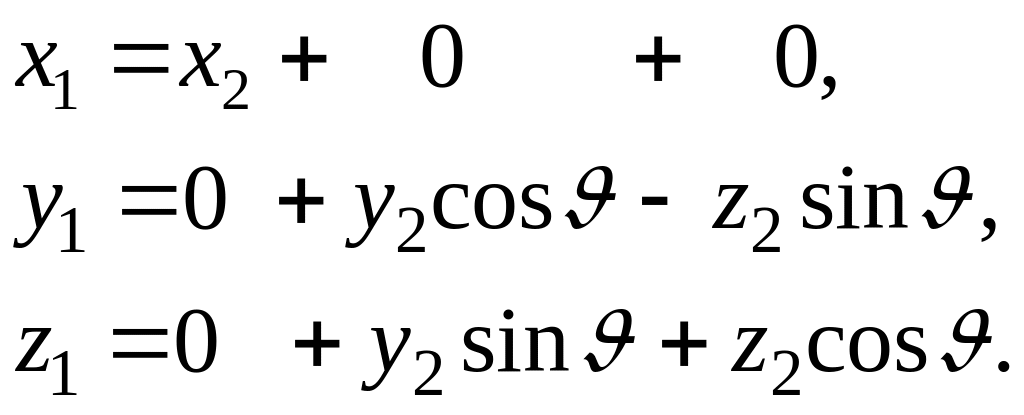(4.4)

Рис.4.4.2

2.2) Формулы преобразования координат от системы к системе

в матричной форме (рис.4.5.2)

или , (4.5)

где – матрица, транспонированная к матрице , задающей пре образование поворота от осей системы к осям системы

вокруг первой из координатных осей на угол крена , при этом

= =СЕ, и называется поворотной матрицей;

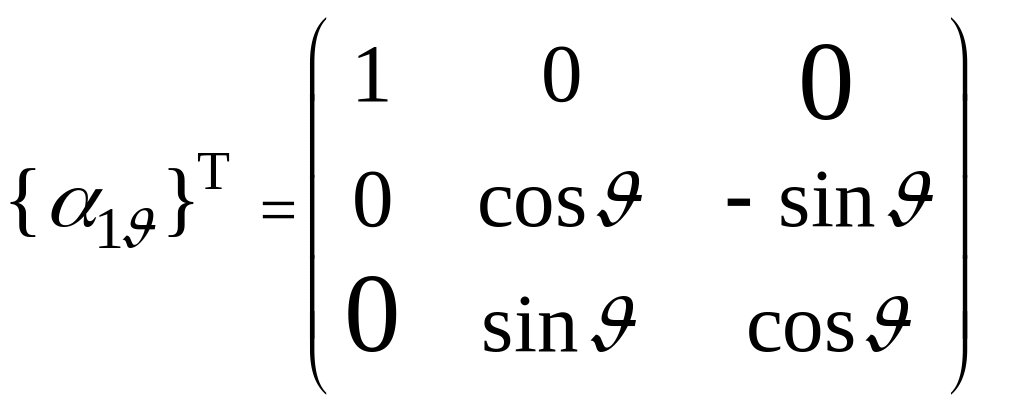(4.6)

.

Рис.4.5.2

3  Третий поворот системы вокруг второй из координатных осей на угол рыскания (рис. 4.4.3) и (рис. 4.5.3*), причем , в результате чего приходим к системе Cxy связанной с твердым телом.

3.1) Формулы преобразования координат от системы к системе Cxyz связаны следующими соотношениями (рис.4.4.3):

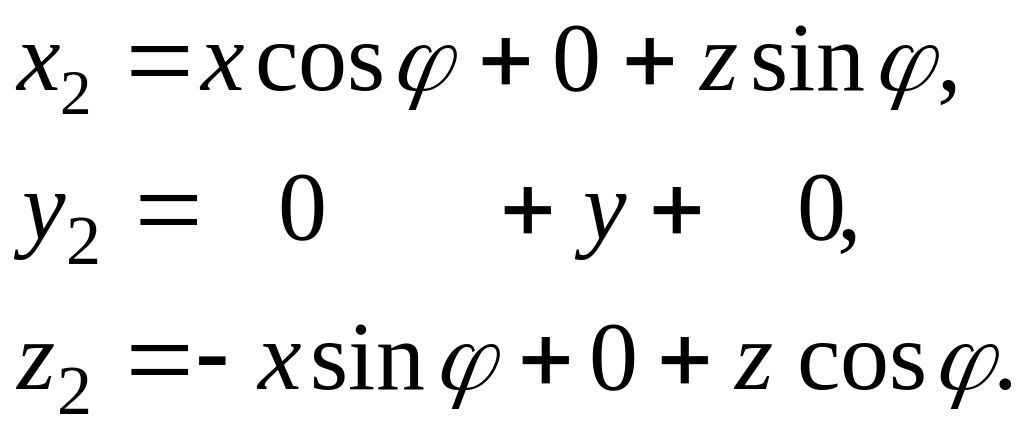( 4.7)

Рис. 4.4.3

Рис.4.5.3

3.2) Формулы преобразования координат от системы к системе в матричной форме (рис.4.5.3):

или 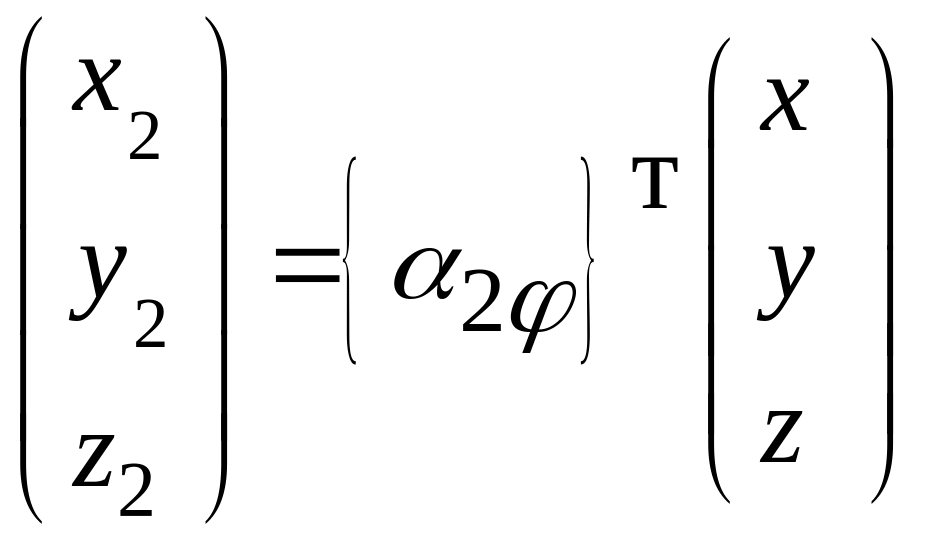. (4.8)

Причем поворотная матрица {_2}^т – это матрица, транспонированная к матрице {_2}, задающей преобразование поворота от осей системы к осям системы Cxyz на угол рыскания вокруг второй из координатных осей = , имеет вид

. (4.9)

Для любой точки М тела с координатами x, y, z в подвижной системе координат, жестко связанной с телом, и с ее же координатами X, Y, Z – в неподвижной системе координат можно установить взаимосвязь проекций вектора точки на оси двух систем координат,

(4.10)

или в матричном виде

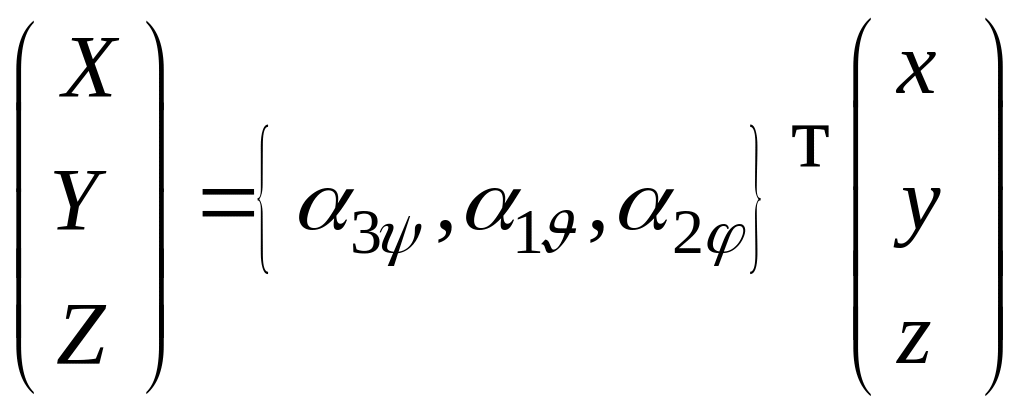или , (4.11)

где углы Крылова являются некоторыми функциями времени: угол дифферента , угол крена , угол рыскания .

Матрица транспонирована к матрице направляющих косинусов , задающей преобразование поворота от осей неподвижной системы CXYZ к осям подвижной системы Cxyz, неизменно связанной с кораблем. Очевидно, что при движении тела координаты x, y, z остаются постоянными в отличие от координат X, Y, Z.

Подставляя в (4.2) соотношения (4.5) и (4.8), получаем:

. (4.12)

Сравнивая (4.11) и (4.12), находим, что искомая матрица является произведением трех поворотных матриц

= =

= =

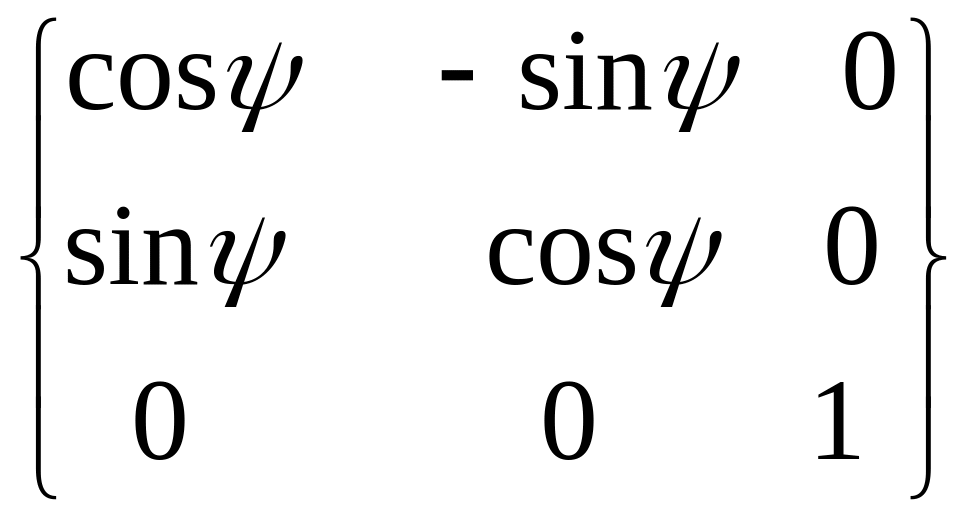
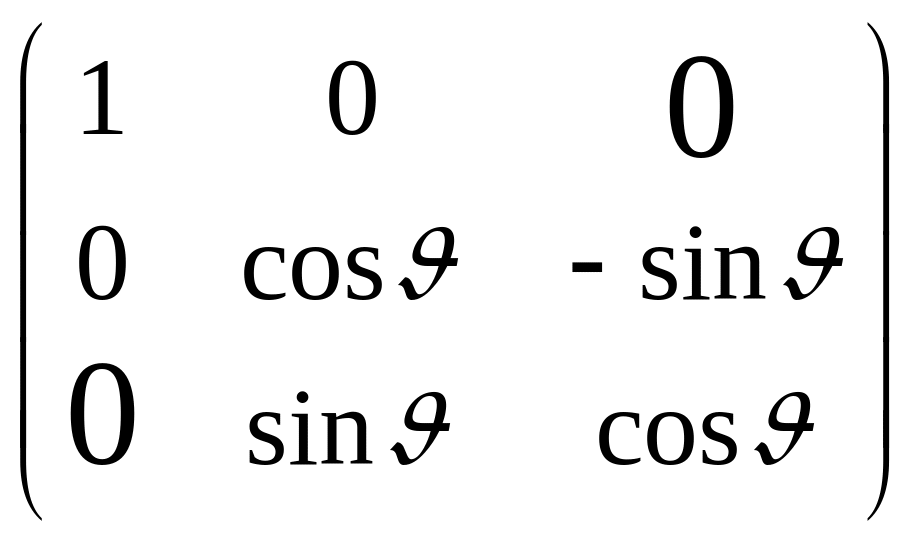
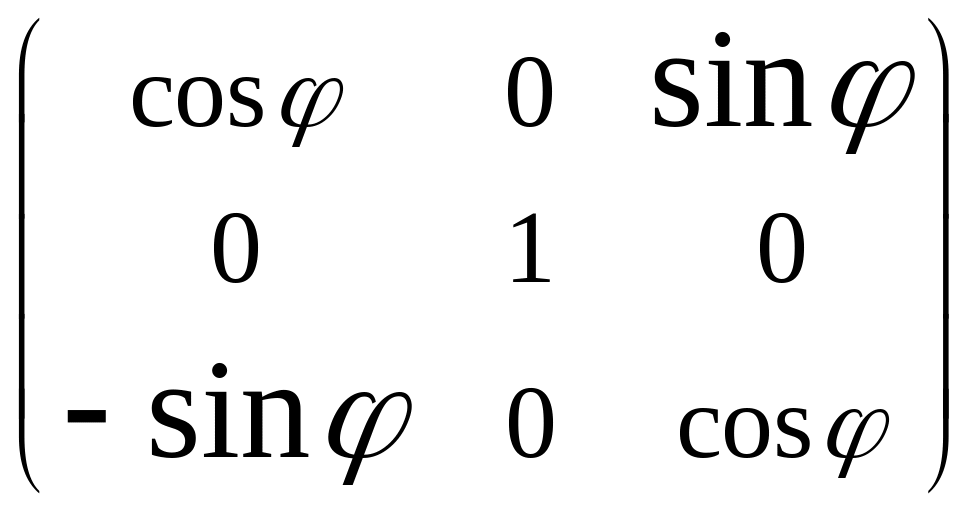. (4.13)

Подставляя в (4.2) соотношение (4.5), получаем промежуточное соотношение, которое может понадобиться в дальнейшем, [X] = [x₂]. Промежуточная поворотная матрица = находится как произведение двух матриц поворота:

= =

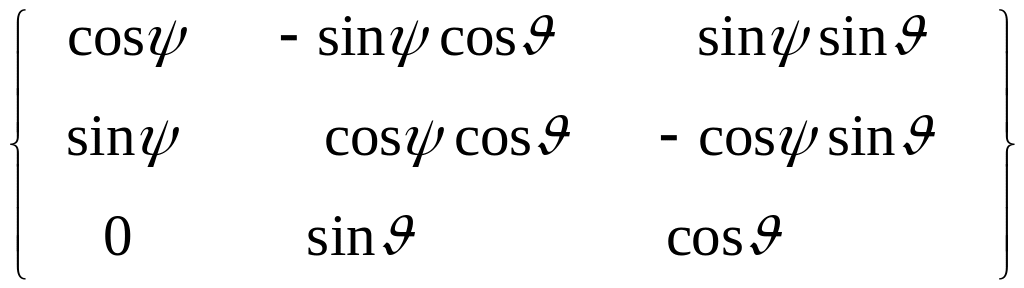= = (4.13a)